Пересечение множеств.
Множество С, состоящее из всех тех и только тех элементов, которые принадлежат каждому из данных множеств А и В (рис 1), называется пересечением множеств А и В и обозначается А ∩ В.
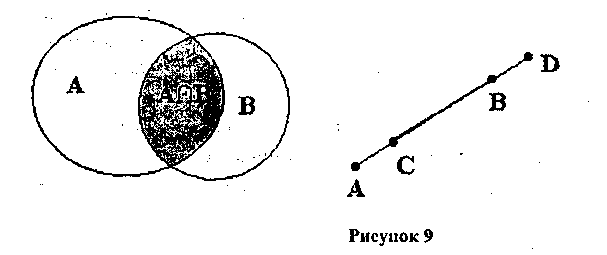
Два множества, пересечение которых является пустым множеством, называются непересекающимися множествами.
Пересечение множеств является операцией, для которой имеет место переместительный 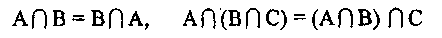 и сочетательный законы:
и сочетательный законы:
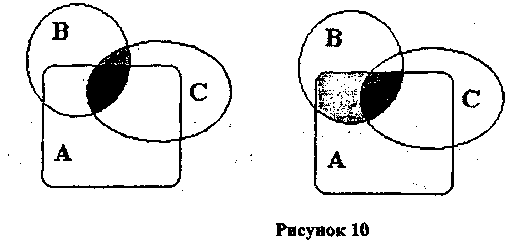
Справедливость этих законов следует из определения пересечения множеств (рис 9,10)
Объединение множеств.
В практической деятельности человека часть встречается операция объединения двух или нескольких множеств в одно новое множество. Например: множества - студенческие группы объединя ются во множество - училище. Операцию объединения множеств обозначают знаком 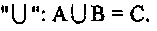
Суммой, или объединением, двух множеств А и В называется такое множество С, которое состоит из всех элементов множеств А и В и только из них.
Если множества А и В имеют общие элементы, то каждый из этих общих элементов берется во множестве С только один раз.
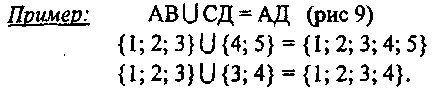
. Дополнение до множества.
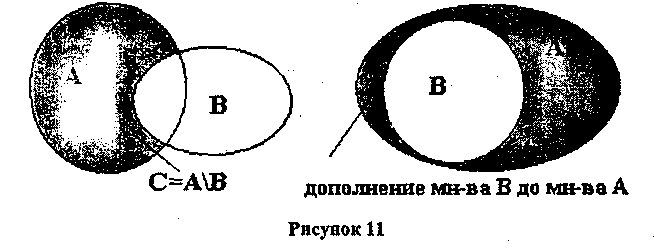
Пусть даны два множества А и В. Множество, которое состоит из всех элементов множества А, не принадлежащих множеству В, называется разностью множеств А и В и обозначается А \ В (рис 11).
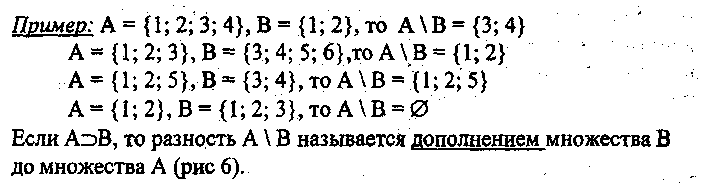
Если А 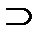 В, то разность А\В называется дополнением множества В до множества А.
В, то разность А\В называется дополнением множества В до множества А.
Прямое произведение двух множеств.
Прямым произведением множеств А и В называется множество, элементами которого являются все упорядоченные пары (х, у), в которых первым компонентом является элемент из А, вторым компонентом - элемент из В. Прямое произведение множеств А и В обозначается А х В. Таким образом, по определению
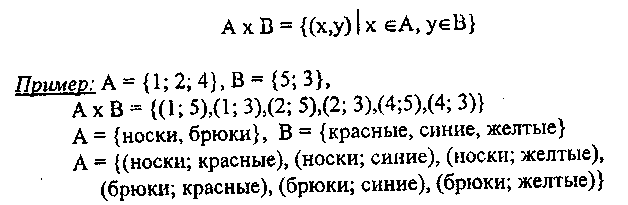
Дата добавления: 2016-06-05; просмотров: 2727;











