Взаимное пересечение прямой и плоскости или поверхности

(2 группа позиционных задач)

а Ç S = М

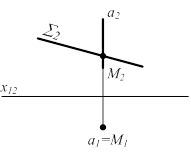
Вариант А. Прямая и плоскость являются проецирующими(рис. 6.5).

а ^ P1 S ^ P2 М Î а; а^P1; М1 = а1; М Î S; S^P2 ; М2 = а2ÇS2

Рисунок 6.5

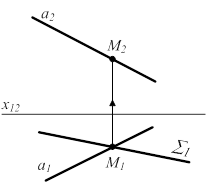
Вариант В-1. Прямая общего положения пересекается с

проецирующей плоскостью (рис. 6.6).

а – общего положения; S ^ P1 аÇS = М МÎа, МÎS, S^P1 Þ М1 = а1ÇS1; МÎа Þ М2Îа2

Рисунок 6.6

Вариант В-2. Проецирующая прямая пересекается с плоскостью

общего положения(рис. 6.7).

а ^ P1; S (с || d) – общего положения. М Î а ; М1 = а1 М Î S , поэтому через т. М проводим произвольную прямую l в плоскости S 11 = l1 Ç с1; 21= l1 Ç d1 M1 Î l1(11,21) ; l Î S l(1;2) Þ M1 Î l1(11;21); М2 Î l2(12,22) или l2 Ç a2 = М2 Для определения видимости на P2 рассмотрим конкурирующие точки 3Î с и 4 Î а. Т.к. точка 3 к нам ближе на плоскости P2 мы видим ее.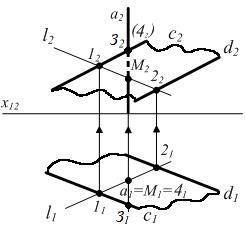

Рисунок 6.7

Вариант С. Прямая и плоскость общего положения

Не рационально использовать замену плоскостей проекций. Задача решается по общему алгоритму:

1) Вводим вспомогательную секущую плоскость Г через прямую а. Вспомогательная плоскость всегда вводится проецирующей: Г^P₁ (или P₂) и обязательно Г Ì а.

2) Находим линию пересечения Г с S : Г Ç S = l (1;2).

Это 1 группа задач варианта В рассмотрена выше.

3) l (1;2) и прямая а лежат в одной плоскости Г; l Ç а = M - искомая точка пересечения прямой а и плоскости S.

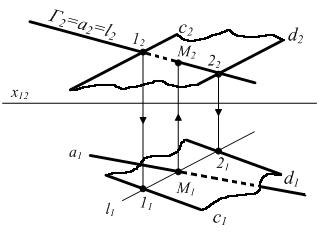
Рассмотрим задачу (рис. 6.8).

а – общего положения; S (c || d) – общего положения. а Ç S = М 1) Г^P2 и G Ì а 2) ГÇS = l (1,2) 1 = Г Ç c 2 = Г Ç d 3) l Ç а = M (l1 Çа1 = M1 ; М2 Ì а2) 4) Для определения видимости необходимо рассмотреть конкурирующие точки прямой а и c или d.

Рисунок 6.8