Алгоритм зависимости длины горизонтального ствола от расхода закачиваемого газа в ПХГ.
1. Задаем исходные данные: 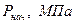 ;
; 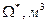 ;
; 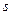 ,
, 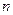 ;
; 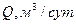 ;
; 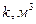 ;
; 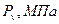 ;
; 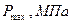 ;
; 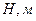 ;
; 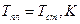 ;
; 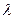 ;
; 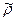 ;
; 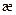 ;
; 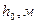 ;
; 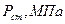 ;
; 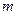 ;
; 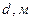 ;
; 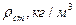 ;
; 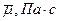 ;
; 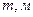 ,
, 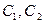 .
.
2. Если выбираем переход с учетом кривизны, то задаем 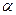 ,
, 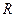 и по формуле
и по формуле 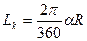 рассчитываем длину дуги кривизны:
рассчитываем длину дуги кривизны: 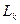 , м.
, м.
3. Если выбираем переход без учета кривизны, то задаем 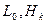 и по формуле
и по формуле 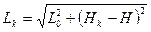 рассчитываем длину дуги перехода
рассчитываем длину дуги перехода 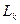 , м.
, м.
4. Принимая 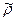 ,
, 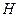 ,
, 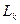 ,
, 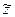 ,
, 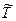 , находим по формулам
, находим по формулам 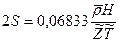 и
и 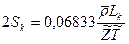 .
.
5. По формуле 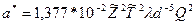 рассчитываем параметр
рассчитываем параметр 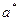 , (кгс/см2)2.
, (кгс/см2)2.
6. По формуле 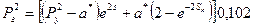 рассчитываем давление в начале горизонтального ствола.
рассчитываем давление в начале горизонтального ствола.
7. Находим 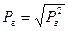 .
.
8. По формуле 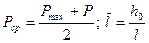 находим среднее пластовое давление.
находим среднее пластовое давление.
9. Рассчитываем фильтрационные коэффициенты для горизонтального ствола, которые имеют вид: 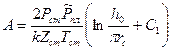 ,
, 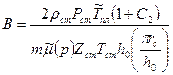 .
.
10. Рассчитываем коэффициент микрошероховатости пласта
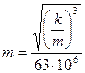 .
.
11. Находим площадь дренирования 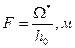 .
.
12. Если аппроксимировать площадь квадратом, тогда расстояние от скважины до контура питания с двусторонним притоком 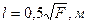 .
.
13. Если аппроксимировать площадь кругом, тогда расстояние от скважины до контура питания с двусторонним притоком 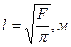 .
.
14. Находим необходимые коэффициенты 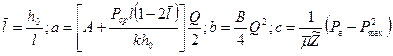 .
.
15. По формуле 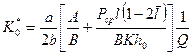 определяем параметр
определяем параметр 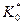 ,1/м.
,1/м.
16. По формуле 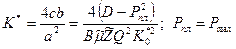 , учитывая,
, учитывая, 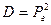 , МПа2, определяем
, МПа2, определяем 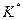 .
.
17. По формуле 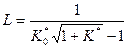 находим
находим 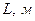 . Откуда следует протяженность горизонтального ствола
. Откуда следует протяженность горизонтального ствола 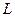 , м.
, м.
18. Построение зависимостей 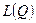 при разных коэффициентах проницаемости, а также зависящих от выбора перехода и от выбора площади дренирования.
при разных коэффициентах проницаемости, а также зависящих от выбора перехода и от выбора площади дренирования.
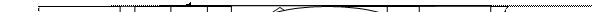 | |||
 | |||
|
|
 | |||
 | |||

Рис. 1.4. Блок-схема алгоритма для расчета длины
горизонтального участка
1.4. Неустановившийся приток жидкости к несовершенной галерее (вертикальной трещине ГРП) и горизонтальной скважине [39]
Рассмотрим одномерное прямолинейно-параллельное движение в обычном пористом пласте. Например, в случае одностороннего притока малосжимаемой жидкости к галерее (рис. 1.5) давление вдоль пласта распределяется по линейному закону:
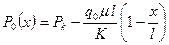 , (1.53)
, (1.53)
где 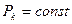 - давление на контуре питания;
- давление на контуре питания;
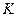 - коэффициент проницаемости пласта по горизонтали;
- коэффициент проницаемости пласта по горизонтали;
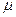 - коэффициент абсолютной вязкости жидкости;
- коэффициент абсолютной вязкости жидкости;
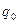 -расход на единицу площади сечения пласта, имеющий размерность скорости;
-расход на единицу площади сечения пласта, имеющий размерность скорости;
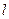 - длина пласта;
- длина пласта;
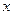 - координата.
- координата.
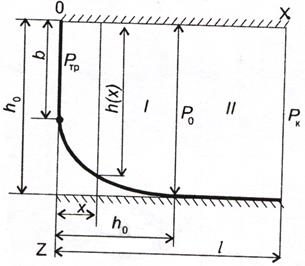
Рис. 1.5. Схема притока к несовершенной галерее
(вертикальной трещине) и горизонтальной скважине
1. Случай 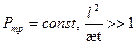
В соответствии с работой [66] для нестационарного притока сжимаемой жидкости в упруго-пористой среде для малых значений 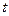 или при
или при 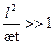
 имеем следующее решение для распределения давления и формулу
имеем следующее решение для распределения давления и формулу
дебита:
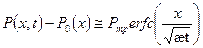 , (1.54)
, (1.54)
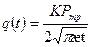 , (1.55)
, (1.55)
где 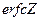 - дополнительный интеграл вероятностей;
- дополнительный интеграл вероятностей;
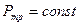 - давление на галерее;
- давление на галерее;
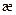 - коэффициент пьезопроводности;
- коэффициент пьезопроводности;
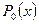 - стационарное значение давления.
- стационарное значение давления.
Решая совместно (1.53) и (1.54) и определяя 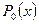 по методу смены стационарных состояний при
по методу смены стационарных состояний при 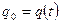 , получаем:
, получаем:
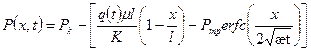 . (1.56)
. (1.56)
Далее рассмотрим приток к несовершенной галерее (щели) в однородно-анизотропном пласте (см. рис. 1.5). Разделим условно область течения на две зоны [27]: I - зона пространственного движения размером по длине, равной толщине пласта 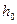 ; II - зона одномерного плоскопараллельного движения. Галерею примем за линию стоков. Если принять
; II - зона одномерного плоскопараллельного движения. Галерею примем за линию стоков. Если принять 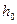 как ширину укрупненной галереи и
как ширину укрупненной галереи и 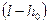 как длину пласта, то для течения в зоне II будет справедливо решение (1.56) при
как длину пласта, то для течения в зоне II будет справедливо решение (1.56) при 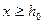 и при замене длины
и при замене длины 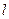 на
на 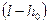 и
и 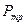 на
на 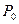 . При
. При 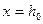 имеем
имеем 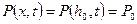 . Тогда получаем:
. Тогда получаем:
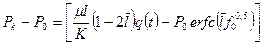 ; (1.57)
; (1.57)
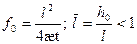 . (1.58)
. (1.58)
Полагая в зоне I движение квазиустановившееся [26], используем решение для одностороннего притока к несовершенной галерее [2], которое в наших обозначениях запишется в виде:
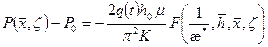 , (1.59)
, (1.59)
где
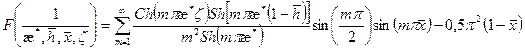 ; (1.60)
; (1.60)
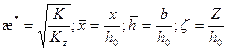 . (1.61)
. (1.61)
Решение (1.59) дает распределение давления (потенциала) в зоне I пространственного движения (см. рис. 1.5).
За расчетное давление на галерее примем усредненное его значение вдоль вскрытой толщины пласта 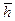 при
при 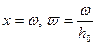 (
( 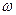 - половина ширины трещины), то есть
- половина ширины трещины), то есть
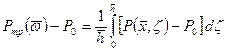 . (1.62)
. (1.62)
Подставляя (1.59) в (1.62), получаем:
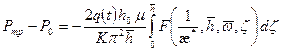 . (1.63)
. (1.63)
Внося значение функции (1.60) при 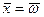 в (1.63) и интегрируя, находим:
в (1.63) и интегрируя, находим:
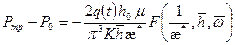 , (1.64)
, (1.64)
где
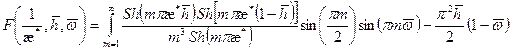 . (1.65)
. (1.65)
Решая совместно (1.57) и (1.64), определяем расход жидкости на единицу площади сечения потока:
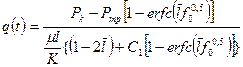 (1.66)
(1.66)
или, учитывая, что
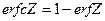 , (1.67)
, (1.67)
из (1.66) получаем:

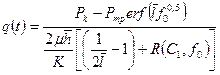 , (1.68)
, (1.68)
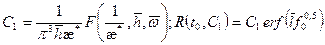 . (1.69)
. (1.69)
Дебит вертикальной трещины протяженностью 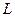 с двухсторонним контуром питания при неустановившемся потоке составит
с двухсторонним контуром питания при неустановившемся потоке составит 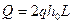 .
.
Здесь 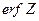 - функция ошибок (затабулирована);
- функция ошибок (затабулирована);
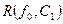 - функция добавочного фильтрационного сопротивления, обусловленная относительным вскрытием пласта трещиной и нестационарным притоком.
- функция добавочного фильтрационного сопротивления, обусловленная относительным вскрытием пласта трещиной и нестационарным притоком.
При 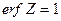 из выражения (1.68) следует формула для неустановившегося притока:
из выражения (1.68) следует формула для неустановившегося притока:
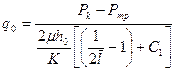 , (1.70)
, (1.70)
где 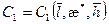 - добавочные фильтрационные сопротивления, обусловленные частичным вскрытием продуктивного пласта трещиной. При
- добавочные фильтрационные сопротивления, обусловленные частичным вскрытием продуктивного пласта трещиной. При 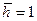 (полное вскрытие) имеем
(полное вскрытие) имеем 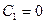 .
.
Примем за сечение горизонтальной скважины эквивалентное сечение 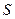 трещиныпо площади, выраженное произведением
трещиныпо площади, выраженное произведением 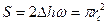 , где
, где 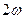 - ширина трещины,
- ширина трещины, 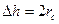 - высота трещины, соответствующая равенству указанных площадей.
- высота трещины, соответствующая равенству указанных площадей.
Отсюда следуют соотношения:

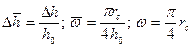 . (1.70')
. (1.70')
2. Случай 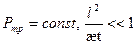
Согласно [1] решение для распределения давления в зоне II запишется в виде:
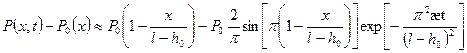 . (1.71)
. (1.71)
На контуре 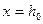 имеем
имеем 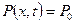 . Учитывая это условие и вводя безразмерные параметры, из совместного решения (1.71) и (1.53) получаем:
. Учитывая это условие и вводя безразмерные параметры, из совместного решения (1.71) и (1.53) получаем:
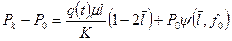 , (1.72)
, (1.72)
где
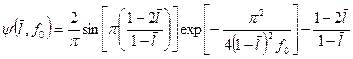 . (1.73)
. (1.73)
Решая совместно (1.64) и (1.72), находим дебит скважины:
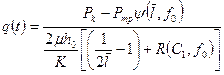 . (1.74)
. (1.74)
На контуре 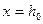 имеем
имеем 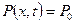 . Учитывая это условие и вводя безразмерные параметры, из совместного решения (1.71) и (1.53) получаем:
. Учитывая это условие и вводя безразмерные параметры, из совместного решения (1.71) и (1.53) получаем:
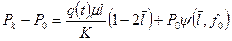 , (1.72)
, (1.72)
где
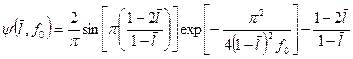 . (1.73)
. (1.73)
Решая совместно (1.64) и (1.72), находим дебит скважины:
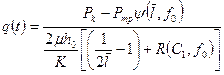 . (1.74)
. (1.74)
3. Случай заданного расхода 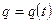
Согласно [66] имеем :
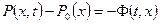 , (1.75)
, (1.75)
где
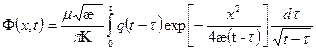 . (1.76)
. (1.76)
Учитывая, что 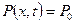 - начальное давление на границе зон, для зоны II
- начальное давление на границе зон, для зоны II 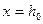 и длине пласта
и длине пласта 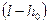 ) получаем:
) получаем:
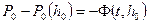 , (1.77)
, (1.77)
где
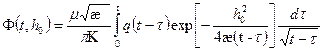 . (1.78)
. (1.78)
Решая (1.77) совместно с (1.53), находим:

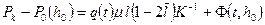 . (1.79)
. (1.79)
Забойное давление как функция времени определится из совместного решения уравнений (1.64) и (1.79):
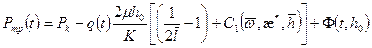 . (1.80)
. (1.80)
При 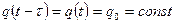 функция (1.78) принимает вид:
функция (1.78) принимает вид:
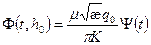 , (1.81)
, (1.81)
где
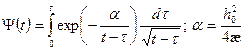 . (1.82)
. (1.82)
Сделаем замену переменных: 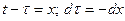 ; пределы меняются: при
; пределы меняются: при 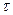
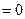 следует
следует 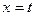 ; при
; при 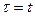 следует
следует 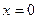 . Интеграл преобразуется к виду:
. Интеграл преобразуется к виду:

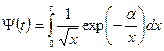 . (1.83)
. (1.83)
Произведем еще раз замену переменных:
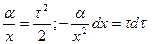 или
или 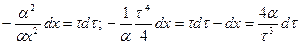 .
.
С учетом этого интеграл (1.83) принимает вид:
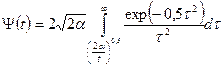 . (1.84)
. (1.84)
Имеется несобственный интеграл [5]:
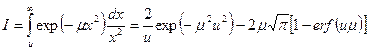 . (1.85)
. (1.85)
Сравнивая (1.84) с (1.85) и, замечая, что в выражении (1.85) 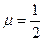 и
и
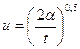 , получаем:
, получаем:
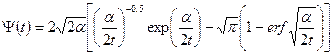 ;
;
учитывая (1.67), находим:

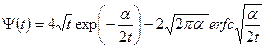 . (1.86)
. (1.86)
При 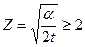 имеем:
имеем:
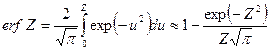 (1.87)
(1.87)
или
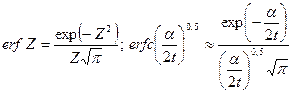 . (1.88)
. (1.88)
Внося (1.88) в выражение (1.86), находим 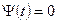 . Таким образом, при
. Таким образом, при 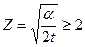 процесс фильтрации становится стационарным, который будет описываться уравнением (1.80) при
процесс фильтрации становится стационарным, который будет описываться уравнением (1.80) при 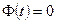 .
.
При 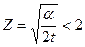 значение функции
значение функции 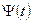 вычисляется по формуле (1.86).
вычисляется по формуле (1.86).
Тогда, преобразуя (1.86) и внося формулу (1.61) в выражение (1.60), получаем:
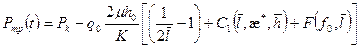 , (1.89)
, (1.89)
где
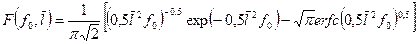 . (1.90)
. (1.90)
Заметим, дебит вертикальной трещины длиной 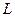 и высотой
и высотой 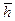 определится как
определится как 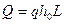 . При
. При 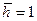 функция
функция 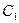 в (1.80) принимает значение
в (1.80) принимает значение 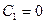 . Для двухстороннего притока дебит увеличивается в 2 раза.
. Для двухстороннего притока дебит увеличивается в 2 раза.
Дата добавления: 2017-04-05; просмотров: 2469;