Первый замечательный предел.
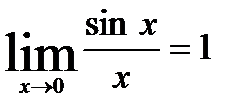
Доказательство:
Рассмотрим единичную окружность и отложим бесконечно малый угол x.
| х |
| у |
| А |
| В |
| С |
| х |
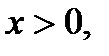 т.е. принадлежит 1 четверти.
т.е. принадлежит 1 четверти.
Очевидны следующие неравенства:
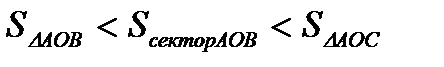
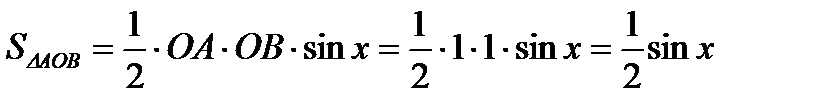
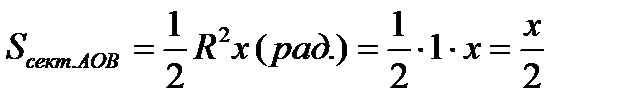
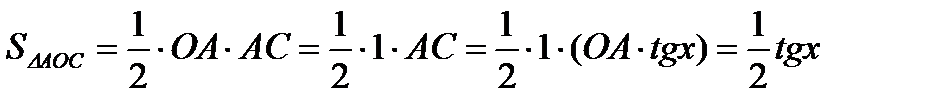
Вернемся к неравенствам: 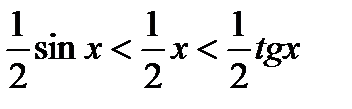
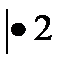
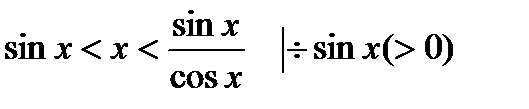
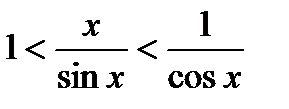
Перейдем к обратным выражениям:
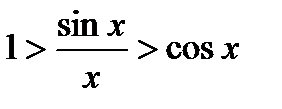
Левая часть неравенства 1 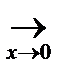 1, т.к.
1, т.к. 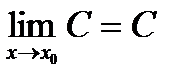
Правая часть неравенства 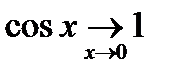
По теореме «о двух милиционерах»: 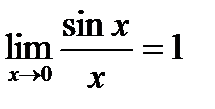
Аналогично при х<0:
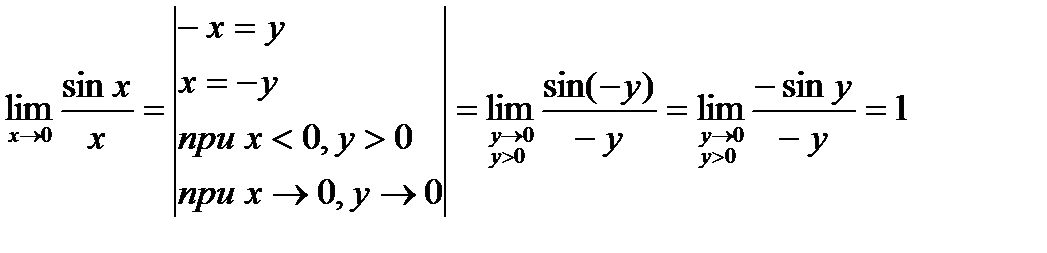
Вместо x может быть любая б/м при х  х0, тогда
х0, тогда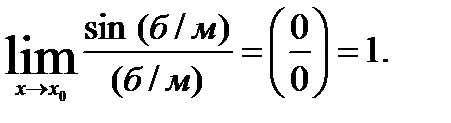
Ч.т.д.
Пример:
1) 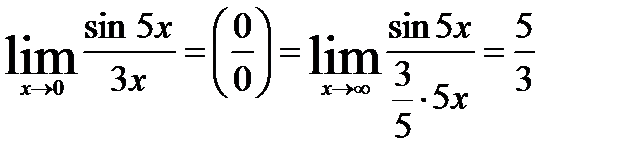
2) 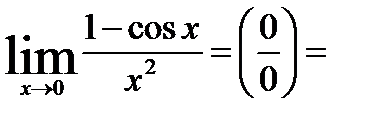
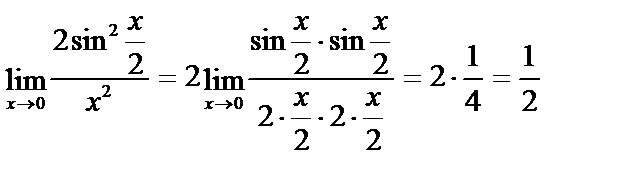

3) 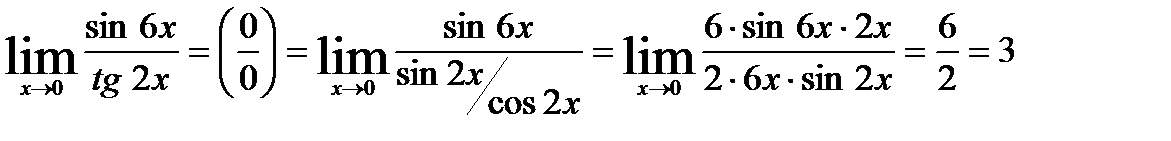
Второй замечательный предел.
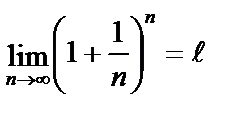
Доказательство:
Вспомним число 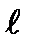 как предел числовой последовательности:
как предел числовой последовательности:
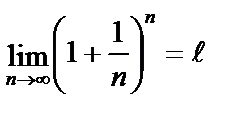
I случай.
Пусть х>1, возьмем n=[x] – целая часть числа х.
n 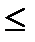 х<n+1.
х<n+1.
Перейдем к обратному выражению:
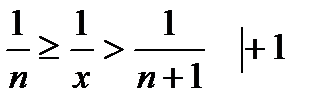
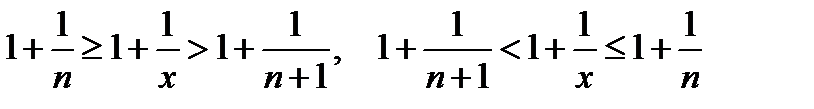
Возведем в степень:
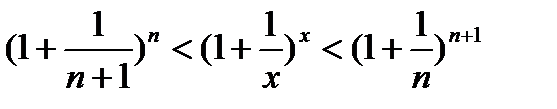
Вычислим предел левой и правой части двойного неравенства:
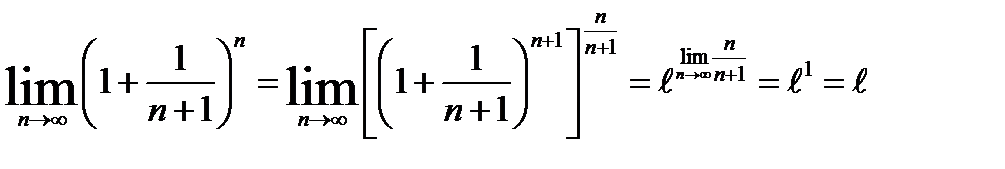
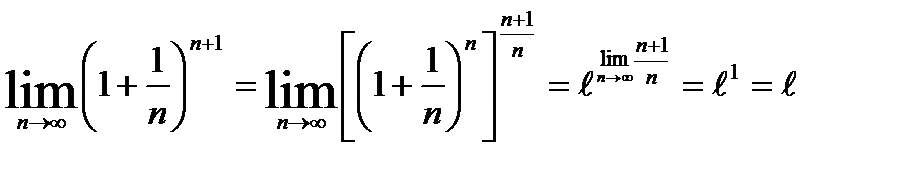
По теореме «о двух милиционерах»:
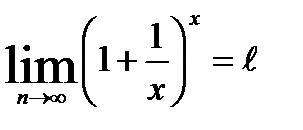
II случай.
Пусть х<-1: проведем аналогичные рассуждения и сделаем замену –х=y, получим:
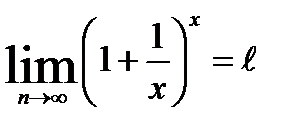 .
.
Ч.т.д.
Второй замечательный предел для функций: 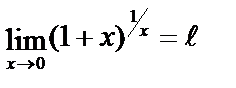
Пример:
1) 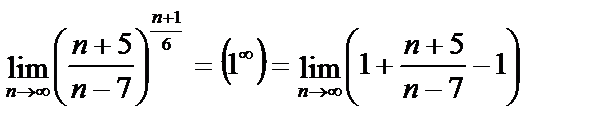 =
= 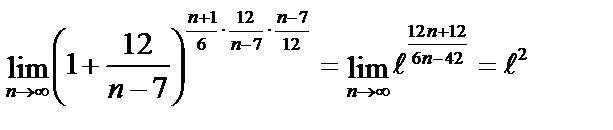
2) 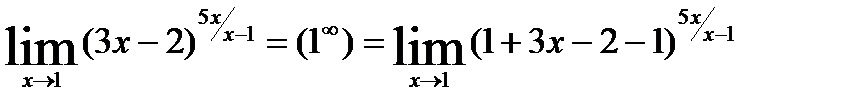 =
= 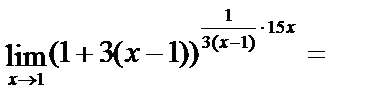
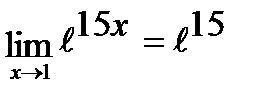
Следствия из второго замечательного предела.
1. 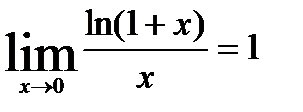
Док-во:
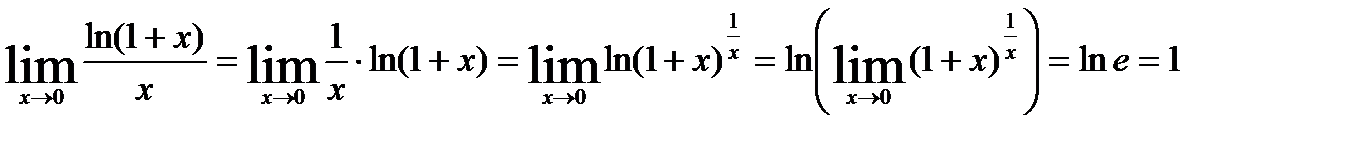
Ч.т.д.
2. 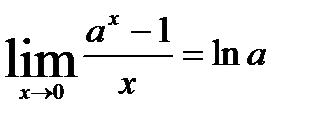
Частный случай: 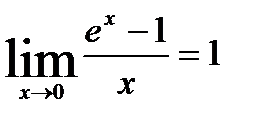
3. 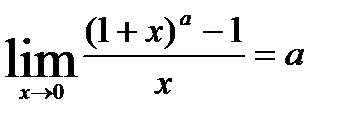
Дата добавления: 2016-06-05; просмотров: 2204;











