Знаки прямоугольных координат в различных октантах
| № октанта | x | y | z | Положение в пространстве |
| I | + | + | + | ЛПВ |
| II | + | - | + | ЛЗВ |
| III | + | - | - | ЛЗН |
| IV | + | + | - | ЛПН |
| V | - | + | + | Пр.ПВ |
| VI | - | - | + | Пр.ЗВ |
| VII | - | - | - | Пр.ЗН |
| VIII | - | + | - | Пр.ПН |
Обозначения в таблице: Л – левый октант; Пр. – правый октант; П – передний октант;
З – задний октант; В – верхний октант; Н – нижний октант.
Лекция 2
ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ
 Прямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и при том только одну.
Прямую линию можно рассматривать как совокупность точек. Из школьного курса геометрии известно, что через две точки можно провести прямую и при том только одну.
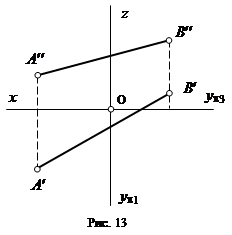
Пусть нам даны на эпюре две точки А и В (рис. 13). Две проекции каждой из этих точек однозначно определяют их положение в пространстве. Если мы соединим одноименные проекции точек, то получим проекции прямой. Точки А и В ограничивают отрезок прямой и определяют положение этой прямой как бесконечной линии.
Таким образом, прямая линия на эпюре может быть задана двумя ее проекциями. По двум проекциям отрезка всегда можно построить его третью проекцию, и притом только одну.
Если прямая не параллельна ни одной из плоскостей проекций, то она пересекает все плоскости проекций и не проецируется ни на одну из них в натуральную величину. Такую прямую называют прямой общего положения. Ни одна из ее проекций не параллельна осям координат. Пример такой прямой изображен на рис. 13.
ТочкА на прямой
Точка принадлежит прямой линии, если ее проекции лежат на одноименных проекциях этой линии.
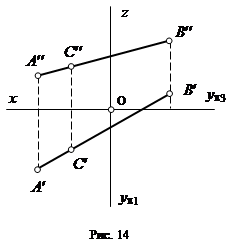 Если на прямой АВ мы выберем какую- либо точку С, то проекции этой точки будут лежать на одноименных проекциях прямой (рис. 14).
Если на прямой АВ мы выберем какую- либо точку С, то проекции этой точки будут лежать на одноименных проекциях прямой (рис. 14).
Вспомним опять школьный курс геометрии: стороны плоского угла делятся параллельными прямыми в пропорциональном отношении. Поэтому если точка делит отрезок прямой в каком-то отношении, то ее проекции делят соответствующие проекции прямой в том же отношении:
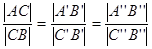 .
.
ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ
Прямая, параллельная одной или двум плоскостям проекций, называется прямой частного положения.
Если прямая параллельна одной плоскости проекций, то одна проекция такой прямой проецируется в натуральную величину, а две другие параллельны осям проекций.
Рассмотрим случаи, когда прямая параллельна одной плоскости проекций.
1) 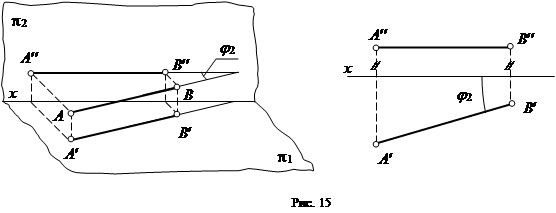 Горизонтальная прямая - прямая, параллельная плоскости p1 (рис. 15).
Горизонтальная прямая - прямая, параллельная плоскости p1 (рис. 15).
Все точки такой прямой удалены от плоскости проекций p1 на одинаковое расстояние, следовательно, у всех точек такой прямой координата z будет одинакова.
 Фронтальная А²В² и профильная А¢¢¢В¢¢¢ проекции горизонтальной прямой всегда перпендикулярны оси z. Горизонтальная проекция отрезка горизонтальной прямой А¢В¢ равна его натуральной величине. Угол между горизонтальной проекцией горизонтальной прямой А¢В¢ иосью x является углом наклона j2 этой прямой к фронтальной плоскости проекций p2.
Фронтальная А²В² и профильная А¢¢¢В¢¢¢ проекции горизонтальной прямой всегда перпендикулярны оси z. Горизонтальная проекция отрезка горизонтальной прямой А¢В¢ равна его натуральной величине. Угол между горизонтальной проекцией горизонтальной прямой А¢В¢ иосью x является углом наклона j2 этой прямой к фронтальной плоскости проекций p2.
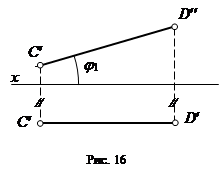
2) Фронтальная прямая - прямая, параллельная плоскости p2 (рис. 16).
Фронтальная проекция отрезка фронтальной прямой равна его натуральной величине; горизонтальная и профильная проекции фронтальной прямой всегдаперпендикулярны оси y.
 Угол j1 между фронтальной проекцией фронтальной прямой и осью x является углом между фронтальной прямой и горизонтальной плоскостью проекций.
Угол j1 между фронтальной проекцией фронтальной прямой и осью x является углом между фронтальной прямой и горизонтальной плоскостью проекций.
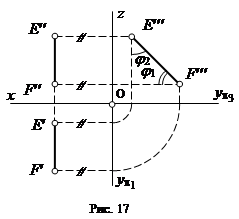
3)Профильная прямая - прямая, параллельная плоскости p3 (рис. 17).
Профильная проекция отрезка профильной прямой равна его натуральной величине; горизонтальная и фронтальная проекции профильной прямой всегда перпендикулярны оси x.
Угол j1 между профильной проекцией профильной прямой и осью y является углом наклона прямой к горизонтальной плоскости проекций; угол j2 между профильной проекцией прямой и осью z - углом наклона прямой к фронтальной плоскости проекций.
Если прямая параллельна двум плоскостям проекций (т.е. перпендикулярна третьей плоскости проекций), то на эти две плоскости проекций прямая проецируется в натуральную величину, а третья проекция представляет собой точку. В зависимости от расположения различают следующие прямые, перпендикулярные плоскостям проекций.
1) Горизонтально-проецирующая прямая – прямая, перпендикулярная плоскости p1 (прямая АВ на рис. 18).
Фронтальная и профильная проекции отрезка горизонтально-проецирующей прямой равны его натуральной величине, а ее горизонтальная проекция представляет собой точку.
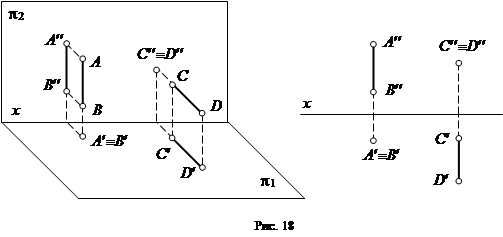 |
2) Фронтально-проецирующая прямая - прямая, перпендикулярная плоскости p2 (прямая CD на рис. 18).
|
|
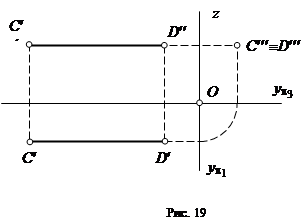
3) Профильно-проецирующая прямая– прямая, перпендикулярная плоскости p3 (рис. 19).
Горизонтальная и фронтальная проекции отрезка профильно-проецирующей прямой равны его натуральной величине, профильная проекция профильно-проецирующей прямой представляет собой точку.
Дата добавления: 2017-01-08; просмотров: 2326;











