МЕТОДЫ ПРОЕЦИРОВАНИЯ

В начертательной геометрии чертеж является основным инструментом решения различных пространственных задач. Поэтому к выполняемому чертежу предъявляются ряд особых требований, среди которых наиболее существенными являются следующие: чертеж должен быть наглядным, обратимым, достаточно простым и точным.

Остановимся более подробно на обратимости чертежа. Под этим свойством понимается точное воспроизведение формы и размеров предмета по его изображению. Действительно для всех видов технических и горно-геологических чертежей это требование является особенно важным, так как при помощи чертежа в машиностроении изготавливается та или иная деталь, в горном деле осуществляется проходка горных выработок, в геологии – оценка запасов полезного ископаемого и т.д.

Основным методом получения изображений в начертательной геометрии является проецирование.

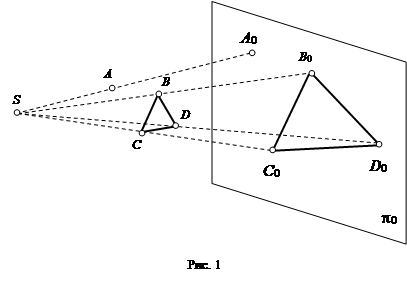
Чтобы понять сущность проецирования, обратимся к рис. 1.

Выбираем центр проецирования - произвольную точку S пространства и поверхность проецирования, не проходящую через точку S, например, плоскость проекций p₀. Для того, чтобы спроецировать некоторую точку A пространства на плоскость p₀, необходимо через центр проецирования S провести проецирующую прямую SA до ее пересечения в точке A₀ с плоскостью p₀.

При этом точка A₀ называется проекцией точки A на плоскости p₀. Проекцией фигуры называется совокупность проекций всех ее точек на выбранную поверхность проецирования (например, на рис. 1 проекцией треугольника BCD на плоскости p₀ является треугольник B₀C₀D₀). Описанный метод проецирования путем проведения проецирующих прямых через точки заданной фигуры и центр проецирования, называется центральным.

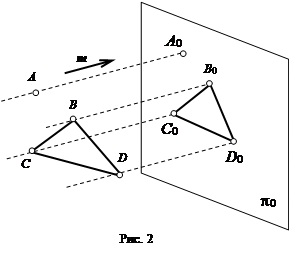В случае, если проецирование осуществляется из бесконечно удаленной точки пространства (рис. 2), то все проецирующие прямые окажутся взаимно параллельными. Этот метод проецирования называется параллельным, а направление m, по которому оно осуществляется, - направлением (вектором) проецирования.

Если направление параллельного проецирования перпендикулярно плоскости проекций, то оно называется прямоугольным или ортогональным. Во всех остальных случаях параллельное проецирование называется косоугольным.

Изображения, полученные при помощи центрального проецирования, обладают хорошей наглядностью, что объясняется устройством зрительного аппарата человеческого глаза. Однако, этот метод имеет существенные недостатки, заключающиеся, во-первых, в сложности построения изображения предмета и, во-вторых, в низких метрических свойствах построенных проекций: вследствие значительных искажений, возникающих при данном методе проецирования, определить истинные размеры предмета весьма затруднительно. Поэтому этот способ имеет ограниченное применение в практике и используется, когда от чертежа требуется прежде всего наглядность.

Несмотря на то, что параллельное проецирование по сравнению с центральным дает меньшую наглядность, параллельные проекции и особенно ортогональные обладают лучшей измеримостью и простотой построения.

Задачи, решаемые методами начертательной геометрии, принято делить на метрические и позиционные.

Метрические задачиимеют цельюопределение размеров различных предметов по их изображению. К таким задачам относятся задачи по определению натуральной величины геометрических фигур, расстояний и углов между ними. В горно-геологической практике – это задачи на определение глубины и угла наклона буровых скважин, угла падения пласта полезного ископаемого, углов между осями горных выработок и т.п.

Впозиционных задачах определяется взаимное расположение различных объектов: точек, прямых линий, плоскостей, пространственных фигур. К этой категории задач относятся, например, установление точки встречи буровой скважины с плоскостью залежи, построение линии пересечения кровли и подошвы пласта полезного ископаемого с горной выработкой и многие другие.

Для быстрого и удобного решения пространственных задач в начертательной геометрии используются несколько систем изображений, особенности которых приведены в таблице 1.

Таблица 1