Плоскости, параллельные двум осям координат

Если плоскость параллельна двум осям координат, то она параллельна той плоскости проекций, в которой лежат эти оси. В нашем примере (рис. 36) плоскость e параллельна осям координат x и y, следовательно, она параллельна горизонтальной плоскости проекций и называется горизонтальной плоскостью.

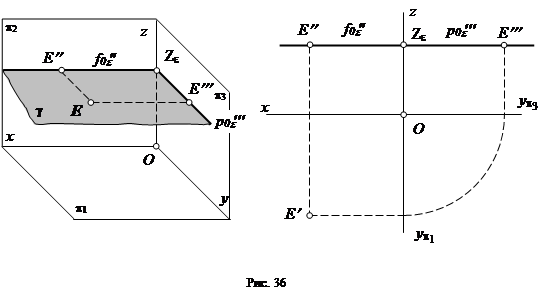
Аналогичным образом можно построить фронтальнуюипрофильнуюплоскости, т.е. плоскости параллельные соответственно фронтальной и профильной плоскостям проекций.

Такие плоскости также являются двояко-проецирующими плоскостями, т.е. перпендикулярными к двум другим плоскостям проекций.

Все, что лежит в такой плоскости в двух плоскостях проекций (к которым она перпендикулярна) проецируется на ее следы, а на третью плоскость проекций (которой она параллельна) – в истинную величину.

Вышеуказанные особенности проецирования точек (объектов), принадлежащих проецирующим плоскостям и плоскостям, параллельным какой либо плоскости проекций, в дальнейшем будут использоваться для оптимизации решения метрических и позиционных задач.

Лекция 4

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ

Прямая может занимать относительно плоскости следующие положения:

а) может лежать в плоскости

б) моет быть параллельна плоскости

в) может пересекать плоскость. Частный случай пересечения – прямая может быть перпендикулярна плоскости.

Прямая лежит в плоскости,если проходит через две точки, принадлежащие этой плоскости.

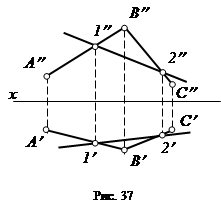
Пусть плоскость задана двумя пересекающимися прямыми АВ и ВС (рис. 37). Проведем в этой плоскости прямую 1-2. Эта прямая лежит в заданной плоскости, так как проходит через две точки 1 и 2,лежащие в этой плоскости.

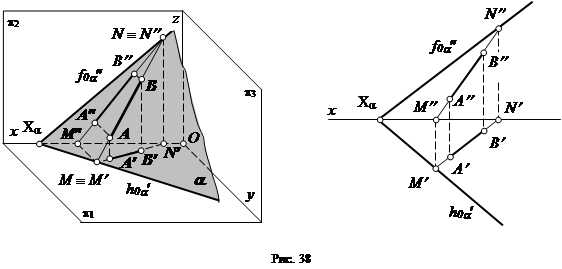
Рассмотрим вариант, когда плоскость заданаследами (рис. 38). В этом случае, если прямая лежит в плоскости, то следы прямой лежат на одноименных следах плоскости.

Это же правило можно сформулировать и иначе: плоскость проходит через прямую, если ее следы проходят через одноименные следы прямой.