Задание студентам на самостоятельную работу.

С помощью MS Excel построить графики:

1. Полигон распределения частот (абсцисса – значение признака; ордината – число вариант);

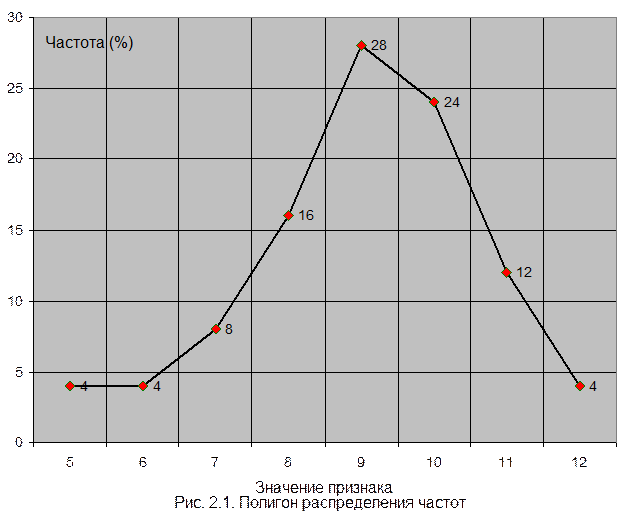
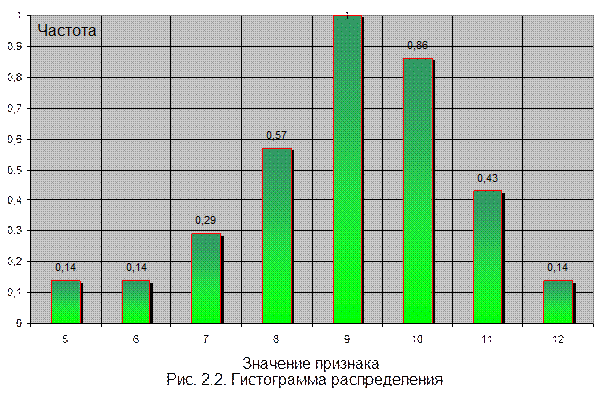
2. Гистограмму распределения удачных бросков (абсцисса – значение признака; ордината – число вариант);

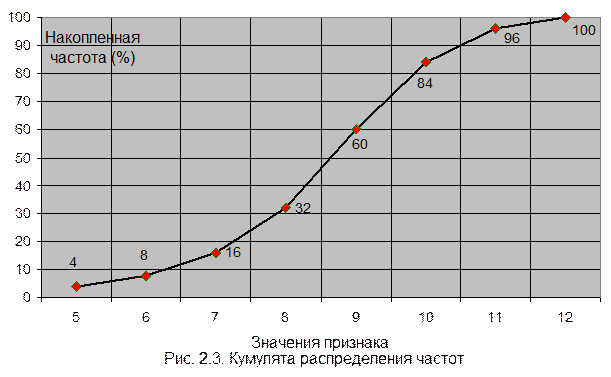
3. Кумуляту распределения (абсцисса – значение признака; ордината – кумулированные частоты).

´Задача 2.3[1]. Исследовалась динамика венозного давления ∆_вд у 8 больных при эпидуриальной анестезии:

15, 20, 20, 25, 30, 30, 35, 55.

Выявить аномальность числа «55» в выборке для P ≤ 0,05 Критериальная статистика вычисляется по формуле В нашем случае D₈ =(55-28,75)/11,66=2,25, что больше табличного D₈ =2,17 для P≤0,05 Вывод: «55» – аномально.		X_i	d	d²
		-13,75	189,06
		-8,75	76,56
		-8,75	76,56
		-3,75	14,06
		1,25	1,56
		1,25	1,56
		6,25	39,06
		26,25	689,06
	M=28,75		SS=1087,50
			δ² =135,94
			SD=11,66
			D=2,25
	P≤0,05		Dtab=2,17

Критические значения статистики D_n

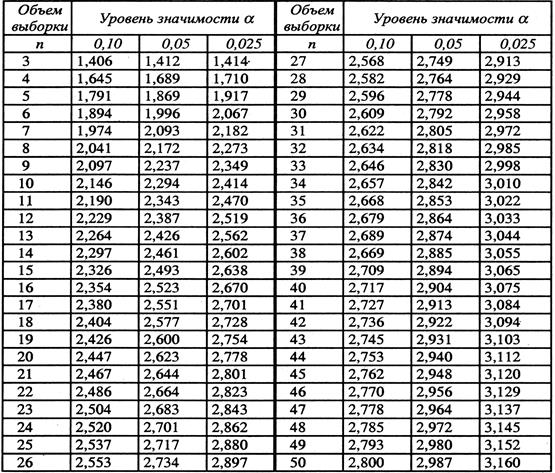
Примечание: Распределение величины D_n получено Карлом Пирсоном (1857 – 1936) и Николаем Васильевичем Смирновым (1910 – 1966). В таблице приведены значения, рассчитанные Н.В. Смирновым и Ф. Граббсом в 1950 г.

´Задача 2.4[5]. Содержание Ca (мг%) в сыворотке крови клинически здоровых павианов гамадрилов.

13,6	12,9	12,3	9,9	12,7	11,7	10,8	10,4	10,9	10,2
14,7	10,4	11,6	11,7	12,1	10,9	12,1	9,2	10,7	11,5
13,1	10,9	12,0	11,1	13,5	11,2	13,5	10,1	14,0	10,0
11,6	12,4	11,9	11,4	12,8	11,4	10,9	12,7	13,8	13,2
11,9	10,8	11,0	12,6	10,0	10,3	12,7	11,7	12,1	13,8
12,2	11,9	11,6	10,6	11,1	10,7	12,3	11,5	11,2	11,5
12,7	10,5	11,2	11,9	9,7	13,0	9,6	12,5	11,6	9,0
11,5	12,3	12,6	12,6	12,8	12,5	12,8	11,4	12,5	12,3
14,5	12,3	12,8	11,7	12,2	12,3	11,6	12,0	13,5	12,5
11,6	11,9	12,0	11,4	14,7	11,3	13,2	14,3	13,2	14,2

Требуется: сгруппировать данные (n = 100) в вариационный ряд (упорядоченные по возрастанию элементы выборки).

1. Устанавливаем величину классового интервала по формуле для выборки объемом 100 и менее единиц

= 0,8

2. Строим таблицу.

Классы по уровню Ca, мг%	8,6-9,3	9,4-10,1	10,2-10,9	11,0-11,7	11,8-12,5	12,6-13,3	13,4-14,1	14,2-14,9
Срединные значения классов	9,0	9,8	10,6	11,4	12,2	13,0	13,8	14,6
Частота
Накопленная частота

3. С помощью MS Excel построим графики:

а) Гистограмму распределения Ca в крови (абсцисса – границы классовых интервалов; ордината – частоты вариант);

б) Кумуляту (абсцисса – значения классовых вариант; ордината – кумулированные частоты).

<1 2 345 6 7 >

Дата добавления: 2020-10-25; просмотров: 647;

Задание студентам на самостоятельную работу.

Публикации по технике и механике

Публикации по биологии

Публикации по информатике

Публикации по строительству

Публикации по физике

Публикации по химии

Публикации по электронике

Публикации по искусству

Публикации по истории

Публикации по медицине

Публикации по педагогике