Пример 6.8.1-1. Найти точку локального минимума функции.

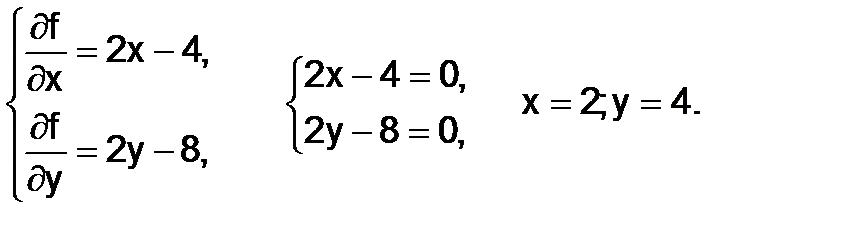
f(x,y) = x² + y² – 4x + 100 – 8y.

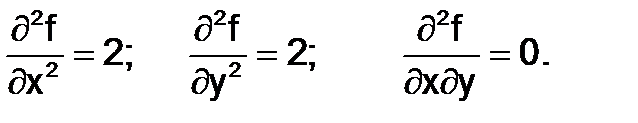
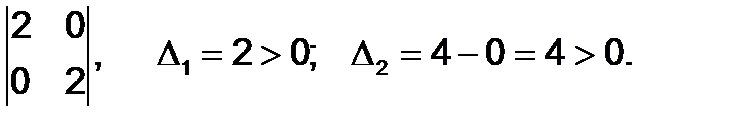
Следовательно, в точке x* = 2 и y* = 4 функция имеет локальный минимум.

Пример 6.8.1-2. Найти точку локального минимума функции
f(x,y)= x²+y²–4x+10xy–8y.

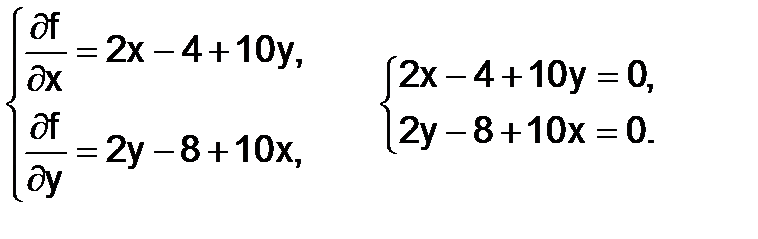
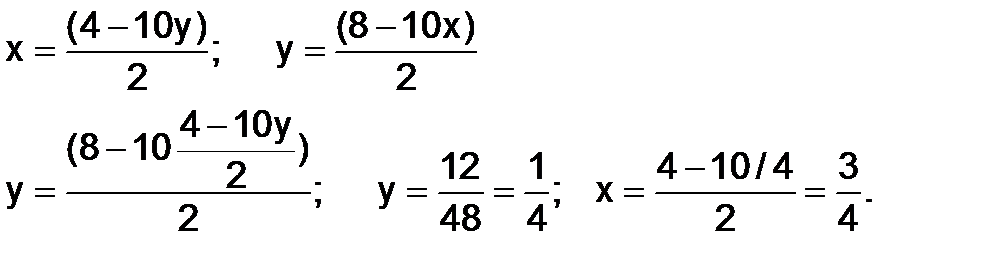
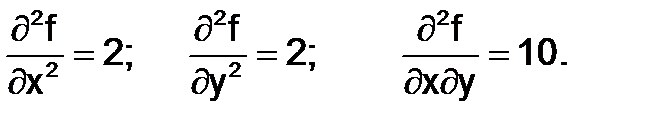
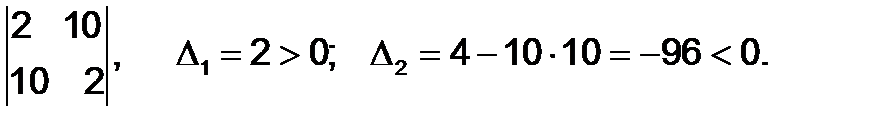
Следовательно, функция не имеет точки локального минимума.

Аналитический метод поиска минимума применяется только для ограниченного круга задач. В основном это связано с необходимостью решения системы нелинейных уравнений, которая, как правило, решается численными методами. Оказывается, гораздо проще сразу решать задачу минимизации численными методами. Рассмотрим некоторые из методов.

Методы спуска

Большинство итерационных методов, применяемых для решения задач безусловной минимизации функции нескольких переменных, относятся к классу методов спуска. Это такие методы, для которых каждая итерация (шаг) приводит к уменьшению значения целевой функции: f(x_k+1)<f(x_k), для всех k³0.

Структура типичного алгоритма метода спуска для функции двух переменных Q(x,y) состоит в следующем:

1.Задается начальная точка (x₀, y₀), принадлежащая области допустимых значений функции.

2.На текущей k-й итерации (k=0,1, …n) определяется вектор 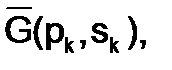задающий направление спуска, причем такой, чтобы для всех достаточно малых значений l>0 (где l- коэффициент, являющийся шагом поиска) выполнялось неравенство:

f(x_k + lp_k, y_k+ ls_k) < f(x_k,y_k).

3.Вычисляется шаг поиска - l_k, для которого выполняется условие п.2, и за очередное приближение к точке минимума принимается точка:

(x_k + lp_k, y_k+ ls_k), где x_k + lp_k = x_k+1, а y_k+ ls_k = y_k+1.

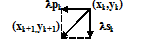
4.Проверяется выполнение критерия окончания итераций. Если критерий метода выполняется, то полагают (x*,y*)»(x_k+1,y_k+1). В противном случае осуществляется переход к п.2 и выполняется следующая итерация.

Последовательность точек х₁, х₂, …, х_k, получаемую методом спуска, называют траекторий спуска.

В градиентных методах спуска направление движения к точке минимума целевой функции совпадает с направлением антиградиента, а направление спуска выбирается по формулам:

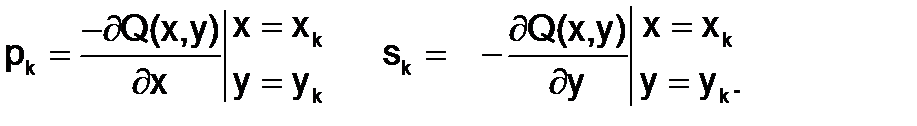
Для использования градиентного метода оптимизации необходимо определить правило выбора шага (l_k) на каждой итерации и правило прекращения итерационного процесса.

При решении вопроса о выборе шага l_k следует учитывать, что выбор малого шага на каждой итерации приведет к малым изменениям аргумента и функции, и, следовательно, к увеличению числа итераций, необходимых для решения задачи. Выбор слишком большого шага l_k может привести не к убыванию целевой функции Q(x,y), а к ее увеличению, и, следовательно, процесс не будет сходиться к точке минимума.