Постановка задачи аппроксимации

Задача аппроксимации (приближения) функции заключается в замене некоторой функции y=f(x) другой функцией g(x, a₀, a₁, ..., a_n) таким образом, чтобы отклонение
g(x, a0, a1, ..., an) от f(x) удовлетворяло в некоторой области (на множестве Х) определённому условию. Если множество Х дискретно (состоит из отдельных точек), то приближение называется точечным, если же Х есть отрезок [a;b], то приближение называется интегральным.

Если функция f(x)задана таблично, то аппроксимирующая функция
g(x, a₀, a₁, ..., a_n) должна удовлетворять определённому критерию соответствия ее значений табличным данным.

Подбор эмпирических формул состоит из двух этапов – выбора вида формулы и определения содержащихся в ней коэффициентов.

Если неизвестен вид аппроксимирующей зависимости, то в качестве эмпирической формулы обычно выбирают один из известных видов функций: алгебраический многочлен, показательную, логарифмическую или другую функцию в зависимости от свойств аппроксимируемой функции. Поскольку аппроксимирующая функция, полученная эмпирическим путем, в ходе последующих исследований, как правило, подвергается преобразованиям, то стараются выбирать наиболее простую формулу, удовлетворяющую требованиям точности. Часто в качестве эмпирической формулы выбирают зависимость, описываемую алгебраическим многочленом невысокого порядка.

Наиболее распространен способ выбора функции в виде многочлена:

,

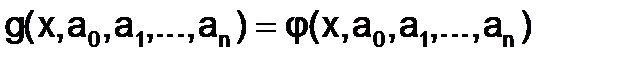где φ(x,a₀,a₁,...,a_n)=a₀φ₀(x)+a₁φ₁(x)+...+a_mφ_m(x), а

φ₀(x), φ₁(x), ..., φ_m(x) – базисные функции (m-степень аппроксимирующего полинома).

Один из возможных базисов – степенной: φ₀(x)=1, φ₁(x)=х, ..., φ_m(x)=х^m.

Обычно степень аппроксимирующего полинома m<<n, a^T=(a₀,a₁,...,a_m) – вектор коэффициентов. Если погрешность исходных данных e, то количество базисных функций выбирается так, чтобы 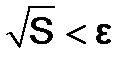. Здесь S – численное значение критерия близости аппроксимирующей функции φ(x, a₀, a₁, ..., a_n) и табличных данных. Отклонения между опытными данными и значениями эмпирической функции

e_i = φ(x_i, a₀, a₁, ..., a_m) – y_i, i = 0,1,2,...,n.

Методы определения коэффициентов выбранной эмпирической функции различаются критерием минимизации отклонений.