Технология решения задач многомерной оптимизации средствами математических пакетов

Нахождение экстремумов функции нескольких переменных проводится аналогично функции одной переменной. Для этого используются функции Maximize(f, y, x) и Minimize(f, y, x), где f – имя функции, а y и x – имена переменных. При использовании функций Мinerr(x,y) или Find(x, y) находятся значения x и y, являющиеся решением системы уравнений, составленной из частных производных исходной функции по x и y. При этом следует помнить, что функция Find дает точное решение, а Мinerr - приближенное. Ниже приведены примеры поиска значения экстремума двумерной функции с использованием функции Minimize(f, y, x).

Пример 6.8.6-1. Решить задачу оптимизации аналитическим методом для функции .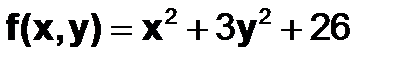

Пример 6.8.6-2. Решить задачу оптимизации для функции двух переменных градиентным методом.

Начальные значения переменных для поиска минимума Решение: xmin=0 ymin=0 f(xmin,ymin)=0

Пример 6.8.6-3. Решить задачу оптимизации с помощью встроенных функций miner( ) .

Построим трехмерный график f(x,y) Построим линий уровня f(x,y)

Пример 6.8.6-4. Решить задачу оптимизации с помощью встроенных функций Maximize (Minimize).

СПИСОК ЛИТЕРАТУРЫ

1. Программа дисциплины «ИНФОРМАТИКА» 2009 г.

1. Шакин В.Н. , Семенова Т.И., Кравченко О.М. ИНФОРМАТИКА: Лабораторный практикум для студентов МТУСИ: Раздел 6. Модели и алгоритмы решения задач численных методов с использованием математических пакетов. – М: МТУСИ, 2009.
2. Электронное учебное пособие и практикум «Информатика» для студентов МТУСИ, 2009.
3. Кравченко О.М., Семенова Т.И., Шакин В.Н. Учебное пособие: Модели решения вычислительных задач (численные методы и оптимизация) по дисциплине «Информатика» для студентов, обучающихся по направлению подготовки «Телекоммуникации»: М.,2003.- 2003.
4. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: М., Высшая школа,1994.
5. Бахвалов Н.С. Численные методы М., Наука, 1973.
6. Банди Б. Методы оптимизации. Вводный курс: М., Радио и связь, 1988.
7. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах: М., Наука, 1972.
8. Демидович Б.Л., Марон И.А. Основы вычислительной математики: М., Наука, 1970.
9. Васильев В.К., Семенова Т.И. Численные методы решения задач на ЭВМ. Уч. пособие: М., МТУСИ, 1993 г.
10. Семенова Т.И., Шакин В.Н. Практикум: Математический пакет MathCad в дисциплине «Информатика»: МТУСИ. М.,2006.
11. Дьяконов В.П. МаhtCad 11/12/13 в математике. Справочник. – М.: Горячая линия – Телеком, 2007. – 958 с.
12. Половко А.М., Бутусов П.Н. MatLab для студентов.- СПб-Петербург, 205.-320с.