Пример 6.7.2-1. Аппроксимировать следующие данные многочленом второй степени, используя метод наименьших квадратов.

<14 151617 18 19 20 >

x	0.78	1.56	2.34	3.12	3.81
y	2.50	1.20	1.12	2.25	4.28

Запишем в следующую таблицу элементы матрицы Грама и столбец свободных членов:

i	x	x²	x³	x⁴	y	xy	x²y
	0.78	0.608	0.475	0.370	2.50	1.950	1.520
	1.56	2.434	3.796	5.922	1.20	1.872	2.920
	2.34	5.476	12.813	29.982	1.12	2.621	6.133
	3.12	9.734	30.371	94.759	2.25	7.020	21.902
	3.81	14.516	55.306	210.72	4.28	16.307	62.129
∑	11.61	32.768	102.76	341.75	11.35	29.770	94.604

Система нормальных уравнений выглядит следующим образом

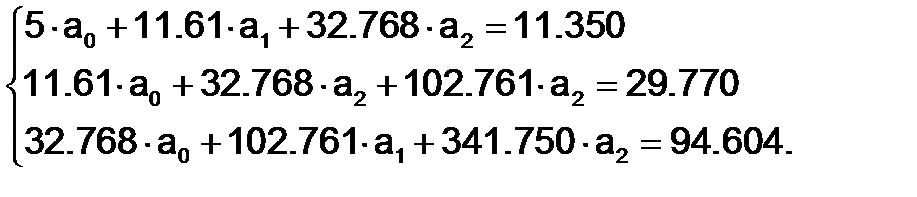
Решением этой системы являются:

а0 = 5.022; а1 =-4.014; а2=1.002.

Искомая аппроксимирующая функция

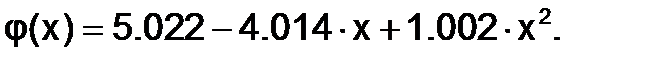
Сравним исходные значения yсо значениями аппроксимирующего многочлена, вычисленными в тех же точках:

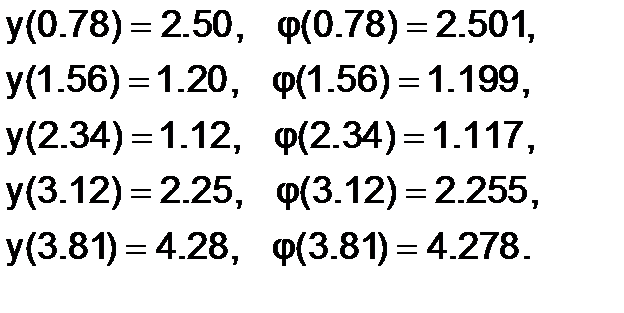
Вычислим среднеквадратическое отклонение (невязку)

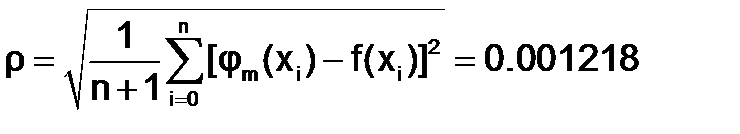Технология решения задач аппроксимации функций средствами математических пакетов

Для аппроксимации функций в Mathcadимеются встроенные функции двух видов: функции, позволяющие увидеть аналитическую зависимость, то есть возвращающие набор аппроксимирующих коэффициентов, и функции, не позволяющие увидеть аналитическую зависимость, а позволяющие только получить значения функции в промежуточных точках.

В Mathcad имеется несколько функций аппроксимации, различающихся способом «соединения» точек (прямой линией или различными кривыми).

<14 151617 18 19 20 >

Дата добавления: 2021-05-28; просмотров: 237;