Тема 6.6. Одномерная оптимизация
Постановка задачи
Метод дихотомии
Метод золотого сечения
Сравнение методов
Технология решения задач одномерной оптимизации средствами
Математических пакетов
Постановка задачи
Задача оптимизации – одна из важнейших составляющих многих инженерных задач. Найти оптимальное решение – означает найти наилучший, в смысле заданного критерия, вариант из всех возможных. При решении задачи оптимизации рассматривается некоторая функция, называемая целевой(иликритериальной), и аргументы (параметры целевой функции), называемые параметрами оптимизации.
По количеству независимых переменных различают задачи одномерной оптимизации (n=1) и многомерной оптимизации (n ³ 2). При этом задача нахождения максимума целевой функции сводится к задаче нахождения минимума путем замены функции f(x) на -f(x), поэтому в дальнейшем будем говорить только о поиске минимума функции, то есть такого x*Î[a, b], при котором f(x*) = min f(x).
В области допустимых значений функция f(x) может иметь несколько экстремумов (минимумов или максимумов - рис. 6.6.1-1). Говорят, что функция f(x) имеет в точке x* локальныйминимум, если существует некоторая положительная величина d, такая, что если ½х – х*½< d, то f(x)³ f(x*), т.е. существует d - окрестность точки х*, такая, что для всех значений х в этой окрестности f(x)³ f(x*). Функция f(x) имеет глобальныйминимум в точке x*, если для всех х справедливо неравенство f(x)³ f(x*). Таким образом, глобальный минимум является наименьшим из локальных.
Рис. 6.6.1-1
Задачей одномерной оптимизации является нахождение точек локального минимума и соответствующих им значений функции, а в некоторых случаях требуется вычислить глобальный минимум. Однако, во всех случаях эта задача сводится к задаче нахождения локального минимума.
Интервал, на котором локализован единственный минимум, называется отрезком неопределенности.
Известно, что необходимым условием существования экстремума дифференцируемой функции f(x) является выполнение равенства f¢(х) = 0. Точка х, удовлетворяющая данному условию, называется точкой стационарности. Достаточнымусловием существования минимума в точке стационарности является выполнение неравенства f¢¢(х)>0, а максимума - f¢¢(х)<0.
Задача одномерной оптимизации имеет единственное решение в том случае, если функция f(x)на отрезке [a;b] имеет только один экстремум. Тогда говорят, что функция унимодальная на отрезке [a;b].
Достаточнымиусловиями унимодальности функции на отрезке [a;b] являются:
1.Длядифференцируемой функции f(x) ее производная f¢(х) -неубывающая.
2.Для дважды дифференцируемой функции f(x) выполняется неравенство f¢¢(х)³0.
Все численные методы одномерной оптимизации применяются только для унимодальных на определенном интервале функций.
Пример 6.6.1-1. Провести исследование функции f(x) = x3 – x + e-x на предмет существования экстремумов.
Вначале проведем графическое исследование. Построим график функции f(x) (рис. 6.6.1-2). Из графика видно, что f(x) имеет две точки минимума: х1 и х2, причем точка х1 – точка глобального минимума. Исходя из графика, можно принять следующие отрезки неопределенности: для точких1 - [-4;-3], а для точки х2 - [0;1].
Рис. 6.6.1-2
Проверим достаточное условие существования минимума на выбранных отрезках:
f¢(x) = 3x2 – 1 – e-x; f¢¢ (x) = 6x + e-x,
f¢(0) < 0, f¢(1) > 0, f¢¢ (x) > 0 для хÎ[0;1],
f¢(-4) < 0, f¢(-3) > 0, f¢¢ (x) > 0 для хÎ[-4;-3].
Условия существования минимума выполнены, поскольку f¢¢(x) > 0 для всех хÎ[0;1] и хÎ[-4;-3]. Следовательно, функция f(x) является унимодальной на выбранных отрезках.
На практике численные методы одномерной оптимизации применяют в следующих случаях:
· значения функции f(x) определены в ходе эксперимента;
· целевая функция очень сложна или не имеет непрерывных производных;
· классические методы поиска оптимального значения не применимы.
Суть методоводномерного поисказаключается в том, что на каждой итерации интервал неопределенности уменьшается и стягивается к точке минимума. Уменьшение отрезка происходит до тех пор, пока на некоторой n-й итерации отрезок неопределенности [bn;an] не станет соизмеримым с заданной погрешностью e, то есть будет выполняться условие |bn-an| < e. Тогда за точку минимума можно принять любую точку, принадлежащую этому отрезку, в частности, его середину.
Простейшим способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Очевидно, что за минимум принимают наименьшее из этих значений – это так называемый метод сканирования. На практике чаще применяют одну из основных модификаций метода – метод прямого перебора с переменным шагом. Суть его заключается в следующем. От начальной точки интервала неопределенности двигаются с начальным шагом до тех пор, пока функция в точках разбиения уменьшается (т.е. функция убывает). Если функция в очередной точке стала возрастать, то происходит сужение интервала неопределенности путем возврата от этой рассматриваемой (которая станет правой границей нового интервала) точки на два шага назад. Полученная таким образом точка будет левой границей нового отрезка. Новый отрезок вновь исследуют таким же образом, но уже с уменьшенным в два раза шагом. Процесс повторяется до момента достижения заданной точности минимума. Это весьма трудоемкий путь. Более эффективными являются методы одномерного поиска с другими способами выбора узлов и сужения интервалов неопределенности.
Рассмотрим, в частности, метод дихотомии и метод золотого сечения.
Метод дихотомии
Пусть дана функция f(x), унимодальная на отрезке [a;b]. Обозначим a0 = aи
b0 = b. Поиск минимума начинают с выбора на отрезке неопределенности [a0;b0] двух симметричных относительно середины точек:
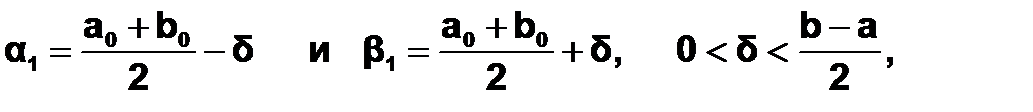 где d - параметр метода.
где d - параметр метода.
Сравнивая вычисленные в точках a1 и b1 значения функций f(a1) и f(b1), в силу унимодальности функции можно провести сокращение отрезка неопределенности следующим образом:
1) еслиf(a1) £ f(b1),тоx*Î[a0;b1](Рис. 6.6.1-3.а);
2) еслиf(a1) > f(b1),тоx*Î[a1;b0] (Рис. 6.6.1-3.b).
а) b)
Рис. 6.6.1-3
Если описанную процедуру принять за одну итерацию, то алгоритм поиска минимума можно описать следующим образом. Опишем k+1 итерацию, исходя из того, что k-й отрезок неопределенности найден [ak;bk]:
1.Вычисляются
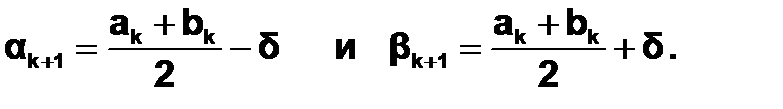
2.Находят значения f(ak+1) и f(bk+1).
3.Находят k+1-й отрезок неопределенности по правилу:
если f(ak+1) > f(bk+1),то x* Î[ak+1;bk],
если f(ak+1) £ f(bk+1),тоx*Î[ak;bk+1]).
Вычисления проводятся до тех пор, пока не выполнится неравенство
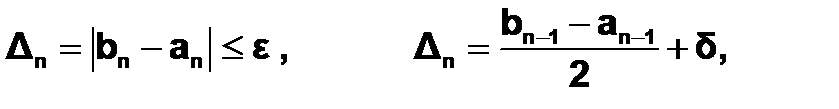
где Dn– длина n-го отрезка неопределенности.
Заметим, что от итерации к итерации Dn убывает и при n®¥ стремится к величине 2d, оставаясь больше этой величины. Поэтому добиться при некотором значении n длины отрезка неопределенности 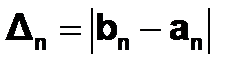 меньше
меньше 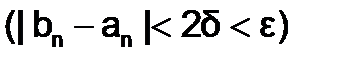 заданной точности можно лишь выбирая 0<d<e/2.
заданной точности можно лишь выбирая 0<d<e/2.
Длину конечного интервала неопределенности, обеспечивающего заданную величину e, можно вычислить по формуле
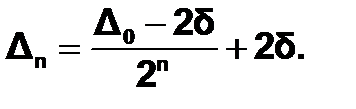
Положив Dn = e, можно определить соответствующее количество итераций:
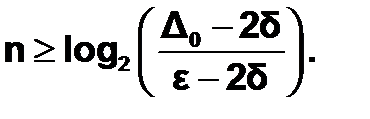
Пример 6.6.2-1. Найти минимум функции f(x)=x3-x+e-х на отрезке [0;1] c точностью e и вычислить количество итераций, требуемое для обеспечения точности.
Выберем d =0.001 и положим a = 0; b = 1; 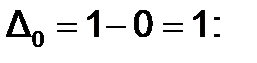
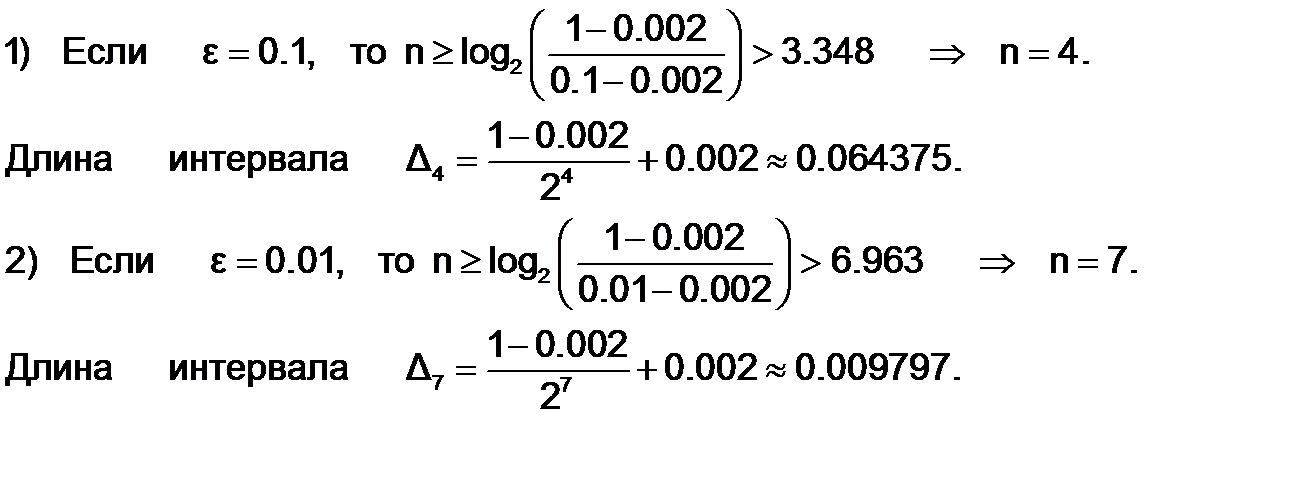
| n | a | b | a1 | b1 | f(a1) | f(b1) | Dn |
| 0.499 | 0.501 | 0.23239 | 0.23067 | 0.501 | |||
| 0.499 | 0.7485 | 0.7505 | 0.14392 | 0.14435 | 0.2515 | ||
| 0.499 | 0.7505 | 0.62375 | 0.6257 | 0.15486 | 0.15413 | 0.12675 | |
| 0.62375 | 0.7505 | 0.68613 | 0.6881 | 0.14040 | 0.14023 | 0.06437 | |
| … | ….. | ….. | ….. | …. | ….. | ….. | …. |
| 0.701719 | 0.71931 | 0.70951 | 0.7115 | 0.13954 | 0.13959 | 0.00979 |
При e = 0.1 x*=0.7183 f(x*)=0.1399, а при e = 0.01 x*=0.7066 f(x*)=0.13951.
Дата добавления: 2021-05-28; просмотров: 492;











