Технология решения обыкновенных дифференциальных уравнений средствами математических пакетов

При решении ОДУ его следует привести к нормальной форме (к виду разрешенному относительно производной исходного ОДУ)

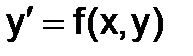
Для ОДУ с разделяющимися переменными исходное уравнение можно привести к виду 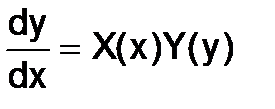, тогда выражение 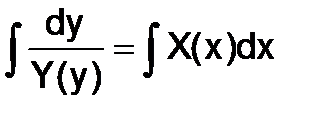задает решение 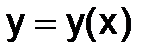задачи Коши с начальными условиями 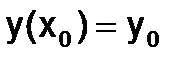как функцию y от переменной х.

Пример 6.5.6-1. Решить ОДУ вида .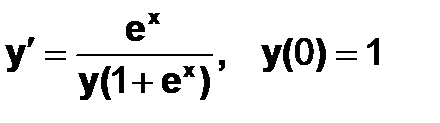

Найдем частное решение данного ОДУ с использованием средств Mathcad, сначала методом разделения переменных, а затем с использованием функции odesolve(x, xk, n), где х – имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования, n – количество шагов, на которых вычисляется решение ОДУ. Результаты подтверждают правильность преобразований.

произвольная постоянная   Аналитическое решение ОДУ Численное решение ОДУ

Аналитическое выражение для решений ОДУ удается получить достаточно редко, поэтому широкое распространение при решении ОДУ получили численные методы.

Пример 6.5.6-2. Решить ОДУ 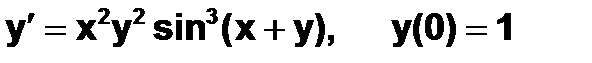на отрезке [0;3] методами Рунге-Кутты с постоянным шагом h=0,6.

В приведенном ниже документе решение, полученное методом Эйлера, обозначено как y1, методом Рунге-Кутты 2-го порядка – y2, а 4-го порядка – y4.

Метод Эйлера Метод Рунге-Кутты 2-го порядка Метод Рунге-Кутты 4-го порядка

В Mathcad нет средств символьного решения ОДУ, но достаточно широко представлены методы численного решения задачи Коши. Для этого предназначена, например, функция rkfixed(y, x₀, x_end, N, D), где y – первоначально равно y₀, x₀ и x_end – начальное и конечное значения аргумента, N – количество проводимых вычислений решения, а переменной D(x,y) должно быть присвоено выражение для вычисления правой части уравнения. Результатом вычислений функции rkfixed( ) служит матрица, в первом столбце которой содержатся координаты узлов x₀ … x_end, а во втором – значения приближенного решения в соответствующих узлах. В функции rkfixed( ) вместо метода Рунге-Кутты используется метод Булирша-Штера. Ниже приведены решения и их графическая иллюстрация, полученные с шагом 0.6 и 0.15.

Пример 6.5.6-3. Решить ОДУ у’= на отрезке [0;3] методами Рунге-Кутты с постоянным шагом h=0.6иh=0.15.

Решение ОДУ 2-го порядка вида у”=F(x, y, z), где z=y’ также может быть получено методом Рунге-Кутты 4-го порядка. Ниже приведены формулы для решения ОДУ:

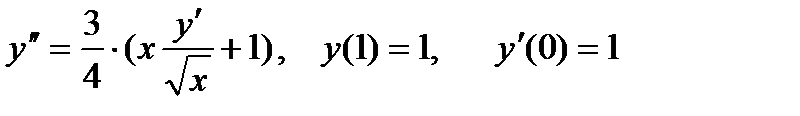
Система Mathcad имеет специальную встроенную функцию для решения дифференциальных уравнений. Она имеет вид: Odesolve ( x , b [ , steps ] ).

Для решения задачи Коши необходимы так называемые начальные условия и указание конца интервала. Эти данные вместе с самим уравнением записываются в блок функции Given, и лишь затем применяется сама функция odesolve( ). Функция имеет ряд особенностей. Если указано число шагов step, то решение выполняется с фиксированным шагом, иначе - адаптивным методом.