Угловая скорость и угловое ускорение

Движение тела (материальной точки) по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги окружности. Положение тела на окружности определяется радиусом-вектором 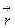, проведенным из центра ок­ружности (рисунок 1.6).

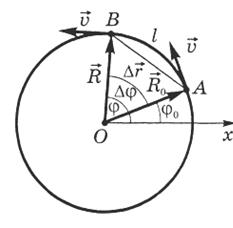
Рисунок 1.6 – Движение материальной точки по окружности.

Модуль радиуса-вектора равен радиусу окружности R. За время Δt тело, двигаясь из точки А в точ­ку B, совершает перемещение Δ 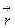, равное хорде АВ, и проходит путь, равный длине дуги l. Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.

Скорость 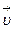движения тела по ок­ружности направлена по касательной к траекто­рии и называется линейной скоростью. Модуль линейной скорости ра­вен отношению длины дуги окружности l к промежутку времени Δt , за который эта дуга пройдена:

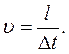(1.13)

Отношение угла по­ворота радиус-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

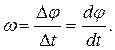(1.14)

Угловая скорость является скалярной физической величиной и в системе СИ выражается в радианах в секунду .

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.

Определить положение тела можно, если известен модуль радиуса-вектора 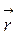и угол φ, который он составляет с осью ОХ (угловая координата).

Пусть в начальный момент времени t₀ = 0 угловая координата равна φ₀, а в момент времени t она равна φ, тогда угол поворота Δφ радиуса-вектора за время Δt = t - t₀ = t равен Δφ = φ - φ₀.

Тогда из последнего выражения мож­но получить кинематическое уравнение движения материальной точки по окружности:

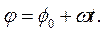1.15)

Данное уравнение позволяет определить положение тела в любой момент времени t.

Учитывая, что из геометрических соображений Δφ = 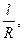получаем:

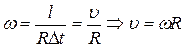(1.16)

Формула (2,6) отражает связь между линейной и угловой скоростью.

Введем еще две характеристики движения материальной точки по окружности: период вращения Т ичастоту вращения ν.

Промежуток времени Т, в течение которого тело совершает один пол­ный оборот, называется периодом вращения:

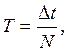(1.17)

где N — число оборотов, совершенных телом за время Δt.

За время Δt = Т тело проходит путь l = 2πR. Следовательно,

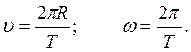(1.18)

Величина ν, обратная периоду, показывающая, сколько оборотов совер­шает тело за единицу времени, называется частотой вращения:

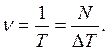(1.19)

Следовательно,

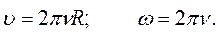(1.20)

При равномерном вращении по окружности модуль скорости движе­ния тела не изменяется по величине, но направление скорости изменяется непрерыв­но. Следовательно, данное движение происходит с ускорением, которое ха­рактеризует быстроту изменения скорости по направлению и называется центростремительным.

Центростремительное ускорение – ускорение тела при его равномерном движении по окружности. Оно направлено всегда к центру окружности, т. е. перпендикулярно мгновенной скорости. Величина центростремительного ускорения находится по формуле

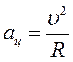. (1.21)

Используя связь между кинематическими характеристиками при равномерном движении тела по окружности, можно получить удобные соотношения для расчета центростремительного ускорения

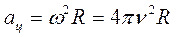. (1.22)

Из двух последних соотношений видно, что в общем случае нельзя однозначно ответить на вопрос: как зависит центростремительное ускорение от радиуса окружности. Все зависит от конкретных условий. Так, например, при движении с постоянной линейной скоростью зависимость обратно пропорциональная, а при движении с постоянной угловой скоростью (частотой или периодом) — прямо пропорциональная.