Лабораторная работа по теме: «Исследование оптимального квантования непрерывных сообщений по уровню».

Преобразуйте стереосигнал в моно и нормализуйте его амплитуду. Измените частоту дискретизации с 44100 на 8000 герц. Фильтровать голосовой сигнал, как это было сделано во второй лабораторной работе, не следует. Спектр сигнала в этой работе нас не интересует.

Сохраните сигнал в текстовом формате в файле под своей фамилией и при помощи текстового процессора Word замените точки в дробных числах запятыми.

Откройте текстовый файл в Excel (файл будет прочитан не полностью). Данные введутся в столбец А. Для удобства последующихрасчетов увеличим масштаб сигнала путем умножения его на 500. Для этого ведите заголовки столбцов А и В и заполните формулы в столбец В (см. рис. 1 и 2).

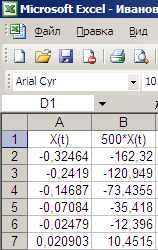
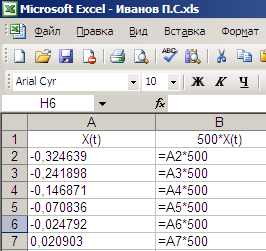
Рис. 1. Данные. Рис. 2. Формулы.

Данные в столбце А находятся в интервале от -1 до +1. Умноженные на 500 (столбец В) - в интервале от -500 до +500.

Из теории следует, что для построения оптимальной шкалы нужно знать диференциальный закон распределения f(x) квантуемого по уровню сигнала. Этот закон используется при вычислении закона компандирования:

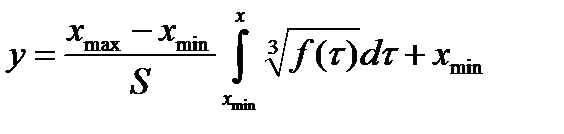
Согласно определению, точки f(x) дифференциального закона распределения равны:

,

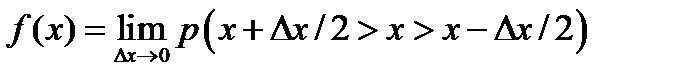где 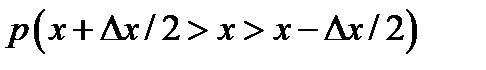- вероятность попадания значения случайного процесса в интервал .

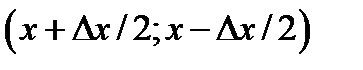Практически, конечно, невозможно устремить 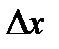к нулю, но можно выбрать 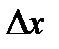достаточно малым. Таким образом можно вычислить с достаточной точностью значения дифференциального закона f(x). В нашем случае можно выбрать 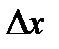=1, что является достаточной малой величиной относительно сигнала, значения которого меняются в интервале от -500 до +500. Осталось найти вероятности попадания зачений сигнала в интервалы единичной ширины. Этот расчет можно выполнить при помощи инструмента Гистограмма табличного процессора Excel.

Исходные данные находятся в столбце В. Для использования инструмента Гистограмма нужны Карманыс единичными интервалами (рис. 3).

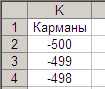
Рис. 3. Интервал Карманов.

Интервал карманов протягивается от -500 до +500.

Запустите инструмент Гистограмма и укажите в его окне положение исходных данных (столбец В) и интервала карманов в столбце К (рис. 4).

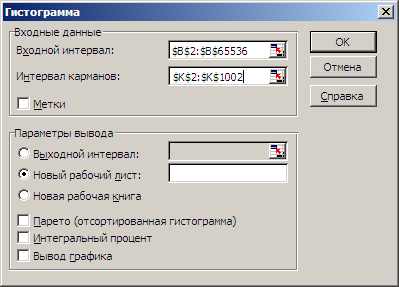
Рис. 4. Содержимое окна Гистограмма.

В результате создается новая страница с результатами работы инструмента Гистограма в столбцах А и В.

На этой странице будет выполнено много вычислений. Добавьте в ее верхнюю часть примерно 22 пустые строки и вставьте в освободившееся пространство формулу закона компандирования (рис. 5).

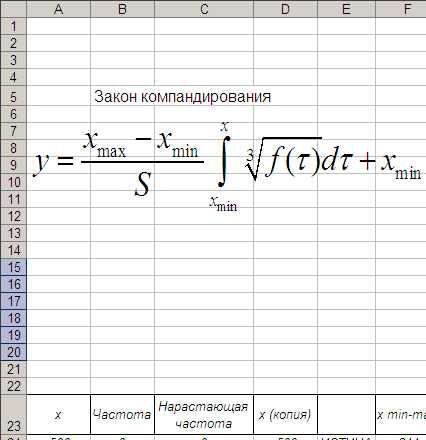
Рис. 5. Изображение нового листа

Замените имя Лист1 нового листа на Шкалы.

Для качественного квантования целесообразно отбросить несколько процентов очень больших и очень малых отсчетов. Для этого образуем в столбце С нарастающую сумму частот, отображаемых в столбце В. Кроме того, скопируйте содержимое столбца А в столбец D и введите заголовки так, как изображено на рис. 6.

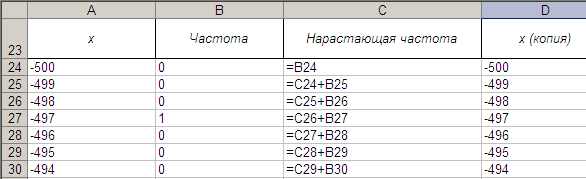
Рис. 6. Столбцы С и D.

Теперь найдем х_min, отсекающее 2% самых малых значений сигнала и x_max, отсекающее 2% самых больших значений сигнала, а также размера шага квантования по уровню равномерной шкалы квантования при 100 шагах (рис.7).

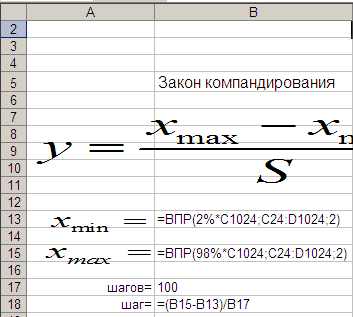
Рис. 7. Формулы расчета х_min, x_max и размера шага квантования по уровню равномерной шкалы квантования.

Для удобства сместим часть данных столбцов А и В вверх так, чтобы данные столбца А измнялись от х_min до x_max.Для этого создадим вспомогательный столбец E и столбцы F и G со смещенными данными из столбцов А и В так, как показано на рис. 8 и 9.

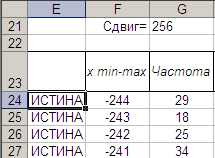
Рис. 8. Столбцы E-G

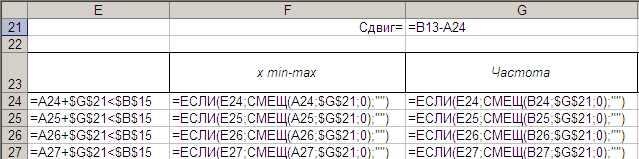
Рис. 9. Формулы в столбцах E-G.

Формулы в столбцах С, E-G копируются до строки 1024.

Теперь можно приступить к вычислению точек диференциального закона распределения f(x) голосового сигнала x(t).

Выше уже сообщалось, что значения этого закона приближенно совпадают с отношением вероятности попадания значения сигнала в некий интервал к ширине этого интервала. Возьмем интервал шириной, равной единице. Тогда приближенное значение закона распределения станет равным вероятности попадания в единичный интервал.

Для нахождения вероятности делим количество попаданий значений сигнала в единичный интервал на общее количество отсчетов. Общее количество отсчетов, значения которых больше х_min и меньше x_max находим в клетке G1025 по формуле =сумм(G24:G1024).

В клетках столбца H находим вероятности – точки закона распределения f(x). По ним в столбце I вычисляем 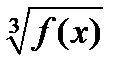. Затем в столбце J - интеграл 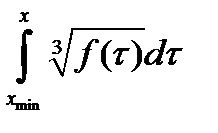(рис. 10, 11).

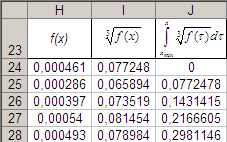
Рис. 10. Вид столбцов H-J

Рис. 11. Формулы в столбцах H-J

Формулы в столбцах H-K следует копировать до строки с номером 24+(x_max - х_min).

Для расчета закона компандирования в клетке К21 подготовим вычисление 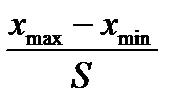, а затем по формуле

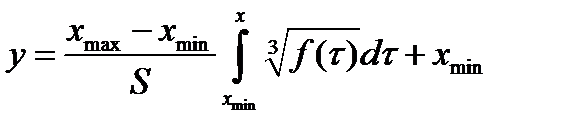
вычислим значения точек закона компандирования (рис. 12, 13).

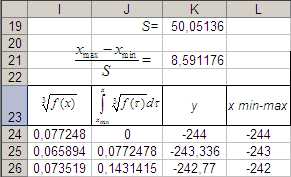
Рис. 12.

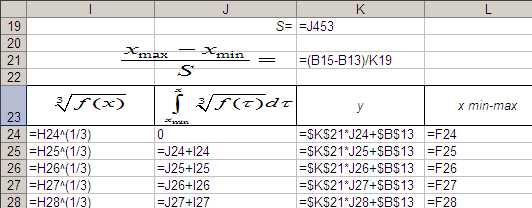
Рис. 13. Формулы.

В столбец L скопируйте столбец F и постройте график закона компандирования (рис. 14).

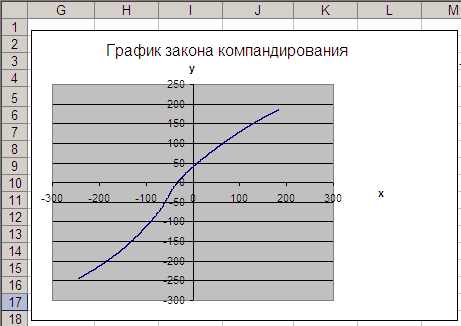
Рис. 14. График закона компандирования

Далее строим равномерную и неравномерную оптимальную шкалы квантования (рис. 15, 16).

Изучите формулы. Необходимо понять их смысл! В случае неудачи – проконсультируйтесь у преподавателя.

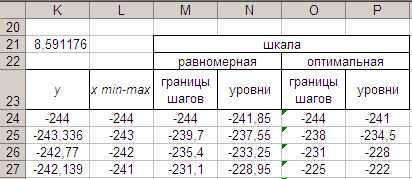
Рис. 15. Результат построения шкал квантования.

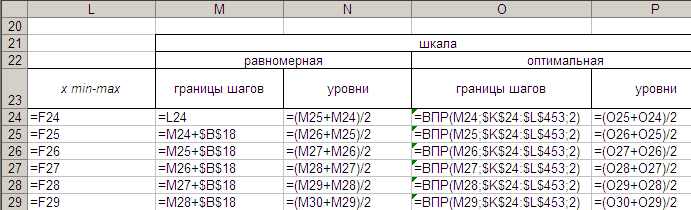
Рис. 16. Формулы, используемые при построении равномерной и неравномерной шкал квантования.

Согласно теории начальные значения шкал должны равняться х_min, а конечные – x_max. Из-за особенностей работы функции ВПР конечное значение оптимальной шкалы окажется несколько меньше. Поэтому вам нужно принудительно приравнять конечное значение оптимальной шкалы x_max.

Теперь оптимальная неравномерная и неоптимальная равномерная шкалы квантования найдены. Используем их для квантования вашего голосового сигнала, рассчитаем дисперсии ошибки в случае квантования при помощи оптимальной неравномерной и неоптимальной равномерной шкал и сравним эти экспериментально найденные дисперсии с их теоретическими значениями.

Все эти вычисления будем делать на листе, названном по имени файла с записью голосового сигнала (в данном примере это лист Иванов П.С.). Перейдите на этот лист.

Сначала пометим строчки с отсчетами, выходящими за границы интервала (x_min, x_max). Для этого заполним столбец С так, как показано на рис. 17, 18.

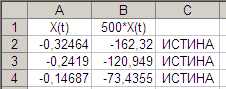
Рис. 17. Значения.

Рис. 18. Формулы.

Теперь строчки со значениями голосового сигнала, попадающими в интервал (x_min,x_max), помечены значением ИСТИНА в клетке столбца С, а строчки со значениями голосового сигнала, не попадающими в этот интервал, значением ЛОЖЬ. Это сделано для того, чтобы исключить крайние значения голосового сигнала.

Теперь все готово для использования ранее найденных шкал для квантования голосового сигнала по уровню. Процес такого квантования и расчет ошибок представлены на рис. 19, 20 (столбцы D-G).

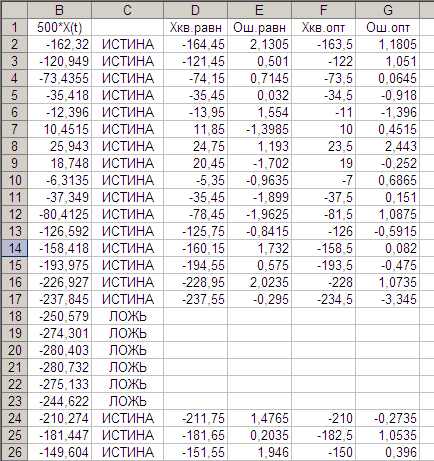
Рис. 19. Результаты применения шкал и расчет ошибок квантования

Рис. 20. Формулы квантования и расчета ошибок

Теперь следует рассчитать теоретические дисперсии ошибок квантования для двух видов шкал (равномерной неоптимальной и неравномерной оптимальной), рассчитать экспериментальные дисперсии ошибок квантования для тех же шкал и сравнить их между собой.

В описываемом примере это сделано на листе Шкалы (рис. 21, 22).

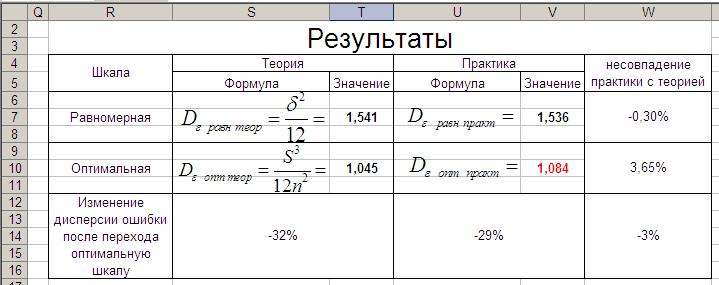
Рис. 21. Результаты расчета теоретических и экспериментальных дисперсий ошибки квантования при использовании равномерной и оптимальной шкал квантования.

Рис. 22. Расчетные формулы для дисперсий ошибки.

Видно хорошее – в пределах нескольких процентов – совпадение теории и практики. Если и в вашем варианте такое совпадение наблюдается – вы справились с заданием, с чем вас и поздравляю!

Результаты работы

На защиту работы должен быть представлены следующие файлы:

5. Wav-файл с записью голоса автора работы;

6. Еxcel-файл с расчетами;

7. Word-документ с титульным листом (см. приложение), теоретически обоснованным описанием хода выполнения работы, ее результатами и выводами.

Литература

1. Мацканюк А.А. Теория информации и кодирования: Учеб. пособие для студентов вузов спец. 351400 «Прикладная информатика (по областям)». –Сочи: РИО СГУТиКД, 2003. -198 с.: 51 рис., 11 табл. –Библиогр: 13 назв.

1. Кэтермоул К.В. Принципы импульсно-кодовой модуляции. -М.:Связь, 1974. -408 с.

2. Советов Б.Я. Теория информации. -Л.: Из-во ЛГУ, 1977. -184 с.

Вопросы для самопроверки

1. Чем задается шкала квантования по уровню?

2. По каким параметрам при построении оптимальной шкалы квантования выполняется оптимизация квантования?

3. Каким образом находится диапазон значений, в который случайная величина попадает с заданной вероятностью?

4. Какую информацию о квантуемом сигнале нужно иметь, чтобы построить оптимальную шкалу его квантования по уровню?

5. Объясните назначение закона компандирования.

6. Как используется формула, описывающая закон компандирования, при построении оптимальной шкалы квантования в данной работе?

7. Как при построении оптимальной шкалы квантования располагаются уровни квантования по отношению к границам интервалов квантования?