Импорт текстовых данных в Excel
Двойным кликом откройте текстовый файл с экспортированные из программы Wavosaur данными (рис. 23).
Рис. 23. Примерный вид данных
Видно, что экспортированные данные представляют собой дробные числа со знаком точка, отделяющим целую часть числа от дробной. Российский стандарт предполагает использование вместо точки запятой. Поэтому для успешного импорта этих данных в Excel для дальнейшей обработки точки нужно заменить запятыми.
Это можно сделать при помощи текстового процессора Word.
Откройте текстовый файл с данными в Wordе и при помощи команды Правка->Заменить… замените по всему тексту точки на запятые (рис. 24, 25).
Рис. 24. Вызов команды Заменить
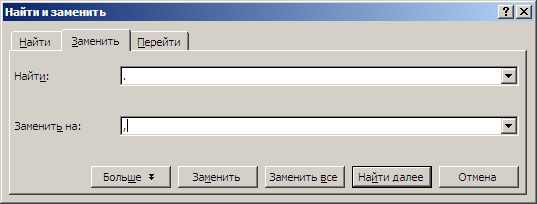
Рис. 25. Окно Найти и заменить. После ввода точки в поле Найти и запятой в поле Заменить на: нажимается кнопка Заменить все.
После замены всех точек на запятые выполняется команда Сохранить (Ctrl+S) и Word закрывается.
Запустите текстовый процессор Excel и откройте только что сохраненный текстовый файл. Вид настроек при вводе в Excel указан на рис. 26.
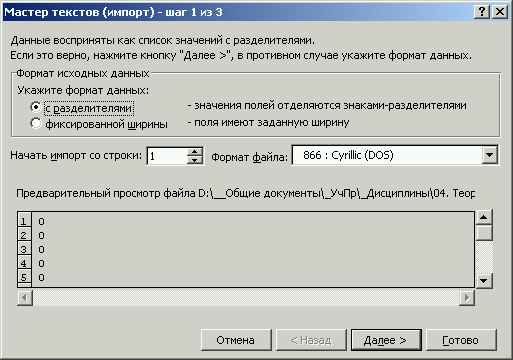
Рис. 26. Настройки окна импорта данных из текстового файла в Excel
В этом окне можно сразу выбирать кнопку ОК.
Если в файле с отсчетами исходного сигнала более 65536 отсчетов, Excel примет только 65536 отсчетов, о чем будет выведено сообщение (рис. 27):
Рис. 27. Возможное сообщение о неполной загрузке файла
В результате будет создана рабочая книга с именем, совпадающим с именем открытого текстового файла. В этой книге будет всего один рабочий лист с тем же именем (рис. 28):
Рис. 28. Возможный вид листа рабочей книги Excel с загруженными данными
Значения отсчетов голосового сигнала размещаются в столбце А. Вследствие ранее выполненной нормализации эти значения будут дробными числами в интервале от -1 до +1.
Excel здесь используется как средство обработки данных. В качестве такового можно было бы, конечно, выбрать и другое средство, например Visual Basic, Delphi, Pascal, C, C++ и т.п.
Непрерывным сигнал сохраненный в рабочей книге Excel можно считать лишь приближенно. На самом деле, конечно, он уже дискретизован. Однако, размеры шагов дискретизации по времени и квантования по уровню здесь настолько малы, что с высокой степенью точности можно считать исходный сигнал, представленный таком образом, непрерывным.
Сначала есть смысл решить вторую более простую задачу – исследование дискретизации-восстановления непрерывного сигнала с применением полиномов Лагранжа и критерия максимального отклонения.
Согласно формулам, выведенным в методическом пособии [1], шаг дискретизации по времени 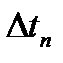 в зависимости от максимального отклонения εm восстановленного сигнала
в зависимости от максимального отклонения εm восстановленного сигнала 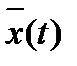 от исходного x(t), а также порядка n используемых для восстановления полиномов Лагранжа рассчитываются по следующим формулам:
от исходного x(t), а также порядка n используемых для восстановления полиномов Лагранжа рассчитываются по следующим формулам:
Таблица 1
Формулы расчета шага дискретизации в зависимости от порядка полиномов Лагранжа, используемых для получения воспроизводящей функции. 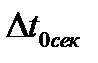 - шаг дискретизации в секундах при использовании полиномов нулевого порядка,
- шаг дискретизации в секундах при использовании полиномов нулевого порядка, 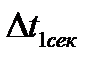 - шаг дискретизации в секундах при использовании полиномов первого порядка
- шаг дискретизации в секундах при использовании полиномов первого порядка
| n | 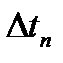
|
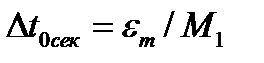
| |
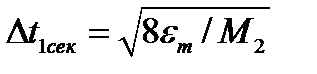
|
Для удобства будем измерять время количеством временных шагов между отсчетами (при частоте взятия отсчетов 8000 герц размер одного временного шага, естественно, равен 1/8000 сек. или 125E-6 сек.; будем называть эти шаги малыми или мелкими). Производная сигнала в какой-то момент времени приблизительно равна разности значений сигнала в соседних отсчетах, деленной на размер мелкого шага.
Здесь надо обратить внимание на то, что данной лабораторной работе применяется два вида дискретизации по времени.
Первый вид дискретизации - дискретизация с частотой 8000 герц (мелкий шаг), примененная при вводе голосового сигнала. Это частота настолько высока, что дискретизированный таким образом сигнал можно с достаточной для решения наших задач точностью считать непрерывным.
Второй вид дискретизации – дискретизация с наименьшей частотой, допускаемой, чтобы достичь заданной точности восстановления исходного сигнала. Шаг и частоту этой дискретизации мы и будем искать. А на основе практического применения дискретизации с этой частотой дополнительно экспериментально мы убедимся в достижении заданной точности.
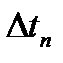 в вышеприведенных формулах – периоды дискретизации второго вида.
в вышеприведенных формулах – периоды дискретизации второго вида.
Для их вычисления необходимо знать:
· максимальное значение абсолютной величины производной первого порядка М1 в случае применения для восстановления исходного сигнала полиномов Лагранжа нулевого порядка;
· максимальное значение абсолютной величины производной второго М2 порядка случае применения для восстановления исходного сигнала полиномов Лагранжа первого порядка.
Приближенное значение производной можно найти как отношение разности последующего и предыдущего отсчетов функции (сигнала), деленной на разность значений (временной шаг) аргумента функции (времени). В нашем случае разность значений аргумента равна 1/8000 сек. или 125E-6 сек.
Откройте рабочий лист с исходными данными (лист с названием <ФИО>). Вам нужно будет создать на нем таблицу примерно следующего вида (рис 29):
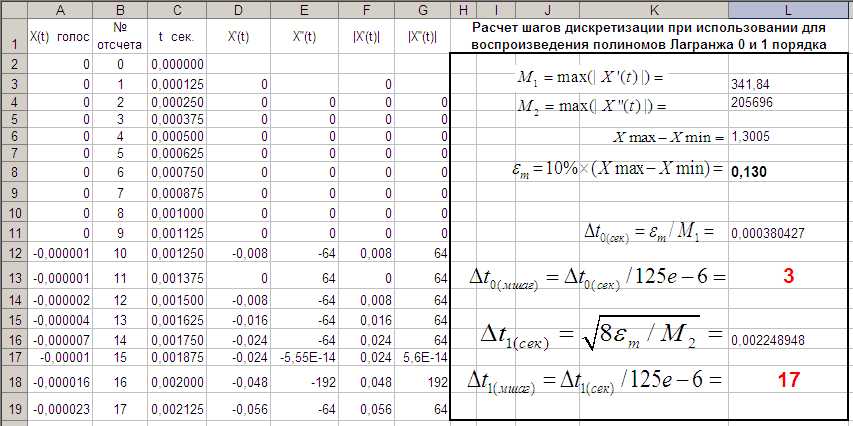
Рис. 29. Примерный вид части таблицы (столбцы А-L)
Значение отсчета в А1 замените заголовком столбца “X(t) голос”.
Введите остальные заголовки в строку 1.
Введите и размножьте формулы так, как показано на рис. 30 и 31
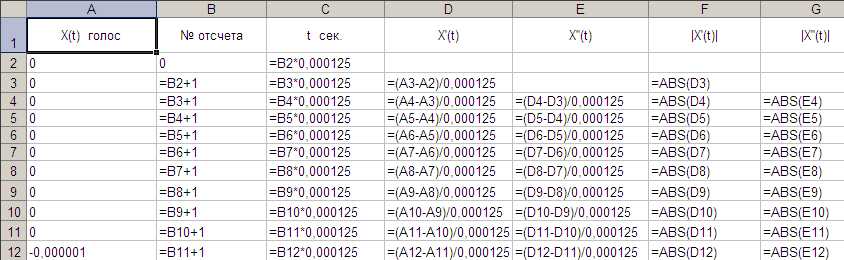
Рис. 30. Расчетные формулы в столбцах A-G (переключение таблицы в режим высвечивания формул и обратно производится нажатием «горячей клавиши» Ctrl + ~).
Формулы в столбцах B-G размножаются до последнего отсчета. В данном примере – до строки 65388.

Рис. 31. Расчетные формулы в столбцах H-L
Максимально допустимое значение ошибки восстановления εm в данной лабораторной работе вам предлагается взять равным 10% размаха дискретизируемого сигнала. Поэтому εm рассчитывается по формуле, вписанной в клетку L6 (см. рис. 31).
Максимальные шаги дискретизации 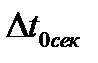 и
и 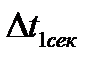 , обеспечивающие ошибку, меньшую εm , находятся по формулам, вписанным в клетки L8 и L12.
, обеспечивающие ошибку, меньшую εm , находятся по формулам, вписанным в клетки L8 и L12.
Нам удобнее работать с шагами, измеряемыми целым числом мелких шагов, которые использовались при вводе голоса в память компьютера. Это временные шаги размером в 1/8000 сек. = 125*10-6 сек. = 125E-6. Пересчет в эти мелкие шаги выполнен формулами в клетках L10 и L18. В результате получаем 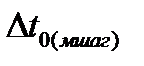 и
и 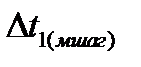 .
.
Теперь займемся проверкой теории практикой для двух вариантов восстановления исходного сигнала по отсчетам. Для этого, используя рассчитанные размеры шагов дискретизации 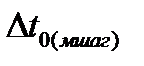 и
и 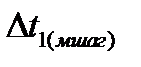 , продискретизируем исходный сигнал, восстановим по полученным отсчетам исходный сигнал (получим воспроизводящую функцию) и найдем максимальную ошибку восстановления. Для этого создадим таблицу, подобную изображенной на рис. 32 с формулами, изображенными на рис. 33.
, продискретизируем исходный сигнал, восстановим по полученным отсчетам исходный сигнал (получим воспроизводящую функцию) и найдем максимальную ошибку восстановления. Для этого создадим таблицу, подобную изображенной на рис. 32 с формулами, изображенными на рис. 33.
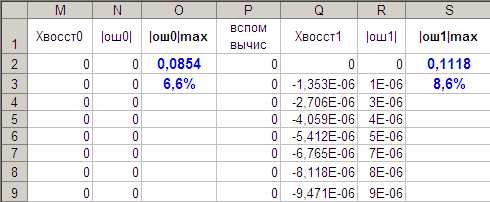
Рис. 32. Таблица для расчета результатов дискретизации и воспроизведения сигнала с использованием полиномов Лагранжа 0 и 1 порядков (результаты).

Рис. 33. Таблица для расчета результатов дискретизации и воспроизведения сигнала с использованием полиномов Лагранжа 0 и 1 порядков (формулы).
Формулы приводятся здесь без пояснений. Обязательно изучите и поймите их. Бездумное копирование формул лишает выполнение лабораторной работы смысла. При необходимости обратитесь к преподавателю.
Сначала вводится первая формула вверху столбца, а затем выполняется ее копирование вниз вдоль столбца. Длины столбцов M, N и P такие же, как длина столбца А. Длины столбцов Q и R – короче на размер шага 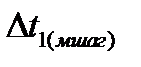 .
.
В итоге в клетках O2 и S2 получается экспериментальное значение максимального отклонения воспроизводящей функции от исходной. При правильно выполненных расчетах и построениях это значение должно быть меньше заданного в клетке L6.
Далее для иллюстрации следует построить графики исходного и восстановленнымх по отсчетам сигналов. Для этого используются отрезки столбцов A, M и Q длиной по 200-300 клеток. В итоге вы получите примерно следующие графики:
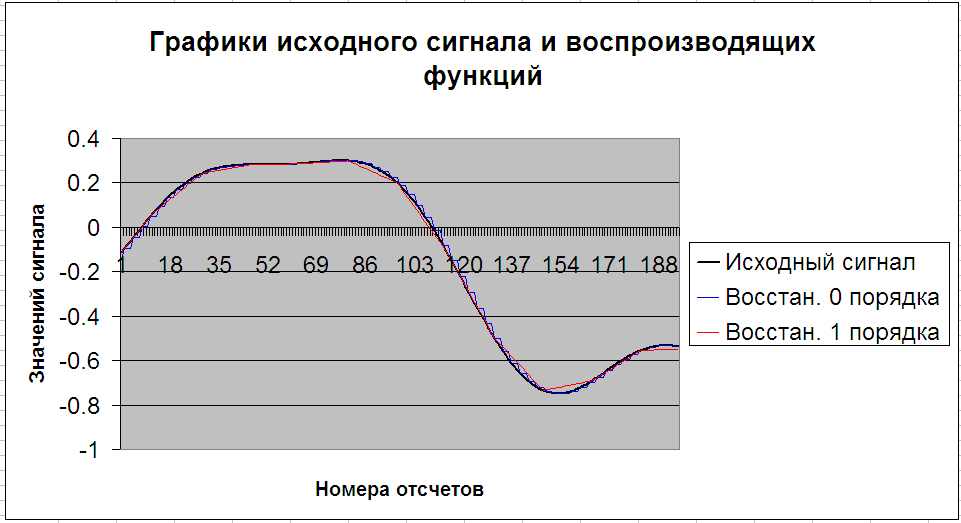
Рис. 34. Графики исходной и воспроизводящих функций при использовании для воспроизведения полиномов Лагранжа 0 и 1 порядков
По результатам решения этой задачи можно сделать вывод, что шаг дискретизации при использовании для восстановления полиномов первого порядка в несколько раз больше, чем шаг дискретизации, если для восстановления пользоваться полиномом нулевого порядка. Рост шага дискретизации – благо, так как при этом уменьшается количество хранимых данных (отсчетов). Однако с ростом порядка полинома растет и сложность вычислений при востановлении.
Теперь можно приступить к решению более сложной первой задачи – исследованию дискретизации-восстановления сигнала по отсчетам, взятым в соответствии с теоремой Найквиста-Котельникова.
Для этого прежде всего следует найти частоту fm, выше которой спектральные составляющие сигнала приблизительно равны нулю.
В моем случае согласно графику спектра на рис. 21 (записывался низкий мужской голос) fm можно взять равным 200 герцам. При этом ослабление частотных составляющих примерно с -50 дб. до -100 дб. равно 50 дб, т.е. в 105 раз. То есть при частотах более 200 герц в рассматриваемом в данном методическом пособии случае спектральная функция практически равна нулю.
Для того, чтобы на практике проверить теорему Найквиста-Котельникова для дискретизации и точного восстановления по полученным в результате дискретизации отсчетам исходного сигнала нужно по fm найти шаг дискретизации Δt.
Пример его расчет приведен на рис. 35. и рис. 36.
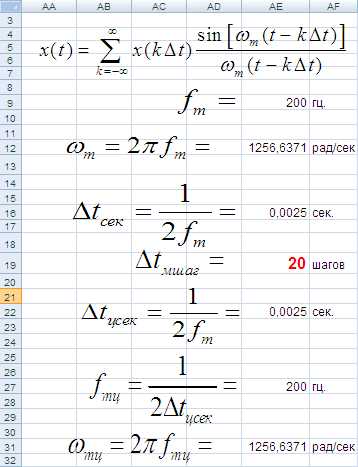
Рис. 35. Расчет шага дискретизации (результат).
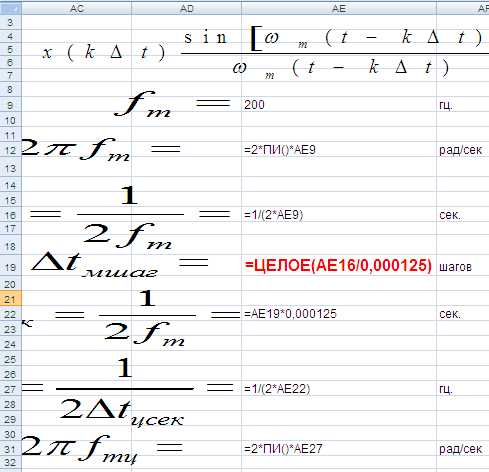
Рис. 36. Расчет шага дискретизации (формулы).
Шаг квантования согласно теореме Котельникова рассчитывается по формуле 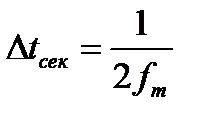 (F5). От временного (в секундах) измерения Δtсек нам удобнее перейти к измерению Δtмшаг в количестве мелких шагов квантования исходного звукового сигнала, равных 1/8000 сек. Это сделано по формуле
(F5). От временного (в секундах) измерения Δtсек нам удобнее перейти к измерению Δtмшаг в количестве мелких шагов квантования исходного звукового сигнала, равных 1/8000 сек. Это сделано по формуле 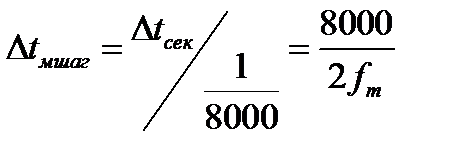 (AD21). А поскольку шаги могут быть только целыми значение, полученное в AD21 округляется до целого. По результату этого округления пересчитываются fmц (AD22) и находится
(AD21). А поскольку шаги могут быть только целыми значение, полученное в AD21 округляется до целого. По результату этого округления пересчитываются fmц (AD22) и находится 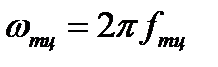 (AD31), использующаяся в формуле ряда Котельникова:
(AD31), использующаяся в формуле ряда Котельникова: 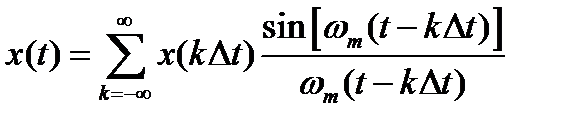
Теперь, когда величины Δt и ωm , используемые в ряде Найквиста-Котельникова найдены, займемся собственно дискретизацией (получением отсчетов – значений сигнала в определенные моменты времени) и восстановлением сигнала по полученным после дискретизации отсчетам. Согласно теореме Найквиста-Котельникова восстановленный с помощью ряда Котельникова сигнал должен совпадать с исходным. Однако на практике это не произойдет, поскольку точно выполнить условия теоремы невозможно. Причин две:
1. из-за того, что все реальные сигналы имеют конечную длительность, их спектры беконечны, т.е. нет частоты fm, выше которой спектр точно равнялся бы нулю;
2. ряд Найквиста-Котельникова имеет бесконечно большое количество слагаемых, что на практике также нереализуемо.
Выполнить условия теоремы Найквиста-Котельникова можно лишь приближенно и это приводит к тому, что воспроизводящая функция будет отличаться от исходной, т.е. будет иметь место ошибка воспроизведения. В этом мы сможем убедиться, анализируя результаты нашего исследования.
Ограничимся учетом лишь 64 членов ряда Найквиста-Котельникова.
Обратим внимание на то, что во всех членах ряда в качестве второго сомножителя используется одна и та же дробь 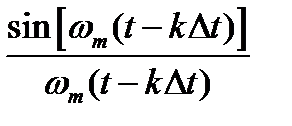 . Это дробь называется функцией отсчетов. Ряд Найквиста-Котельникова состоит из суммы произведений значений отсчетов на соответствующую функцию отсчетов:
. Это дробь называется функцией отсчетов. Ряд Найквиста-Котельникова состоит из суммы произведений значений отсчетов на соответствующую функцию отсчетов:
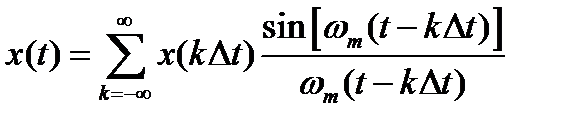
Функции отсчетов связанные с отсчетами отличаются друг от друга лишь смещением вдоль оси времени. Размер смещения равен kΔt.
Для того, чтобы не перегружать компьютер большим количеством повторных вычислений, рассчитаем все точки функции отсчетов один раз и используем эти значения во всех членах ряда.
Анализируя ряд Найквиста-Котельникова можно понять, что при 64 членах ряда функция отсчетов будет использована в интервале значений аргумента t от -64Δt до +64Δt при k=0 (см. иллюстрацию к порядку вычисления ряда Найквиста-Котельникова). В нашем примере Δt=20 (у каждого студента свой Δt). Следовательно для последующих расчетов нам нужно найти значения функции отсчетов при изменении аргумента t от -1280 до +1280 (зависит от Δt). Аргумент t здесь измеряется в количество мелких шагов по 125 мксек (1/8000 сек.) каждый. Для удобства расширим этот интервал до -2000 ÷ +2000 (расширение диапазона допустимо, сужение - нет).
Для подготовки функции отсчетов используем 4 столбца (рис. 37, 38).
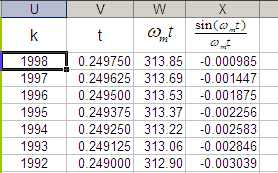
Рис. 37. Вид верхней части столбцов U-X (результаты вычислений)
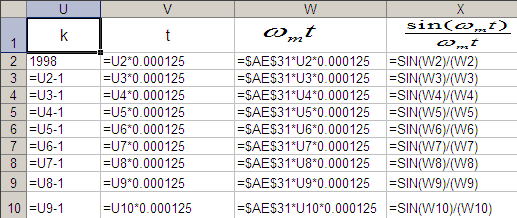
Рис 38. Формулы в верхней части столбцов U-X.
Здесь :
· столбец U – номер мелкого шага (номер меняется от -2000 до 1998), номер 0 для удобства находится в строке 2000;
· столбец V – преобразование номера мелкого шага во время;
· столбец W – вычисления аргумента функции отсчетов при k=0;
· столбец Х – вычисление самой функции отсчетов.
Теперь можно приступить к вычислению членов (слагаемых) ряда Найквиста-Котельникова:
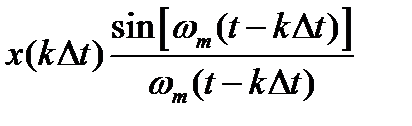
Их у нас будет 64. Эти слагаемые - функции времени t. Слагаемые отличаются значением отсчета 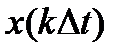 и временным сдвигом
и временным сдвигом 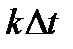 функции отсчетов
функции отсчетов 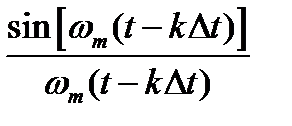
Выделим каждой функции-слагаемому ряда отдельный столбец. Суммирование слагаемых будет означать сложением этих столбцов по горизонтали (вдоль строк). В результате будет найден восстановленный по отсчетам сигнал Х(t).
Для удобства столбцы – слагаемые ряда начнем с 2000 строки таблицы – со строки с нулевым значением аргумента функции отсчетов.
В строке 1998 разместим номера отсчетов – от 0 до 64, а в строке 1999 – сами отсчеты (рис. 39 и 40).

Рис. 39. Номера отсчетов и сами отсчеты

Рис. 40. Формулы вставки в клетку строки номера величины отсчета в зависимости от номера (формула вводится в клетку Z1999 и затем копируется вдоль строки).
В формулах строки 1999 для переноса из столбца А значения отсчета используется функция СМЕЩ. Если она вам неизвестна – прочтите ее описание в справочной системе Help Excel.
Далее в клетку Z2000 вводится формула расчета одной точки функции слагаемого ряда Найквиста-Котельникова (рис. 41).

Рис. 41. Вид формулы в клетке Z2000 расчета одной точки функции слагаемого ряда Найквиста-Котельникова
Первый сомножитель Z$1999 в этой формуле – отсчет 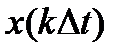 , второй СМЕЩ($X$2000;-Z$1998*$AE$19-$U2000;0) – значение функции отсчетов
, второй СМЕЩ($X$2000;-Z$1998*$AE$19-$U2000;0) – значение функции отсчетов 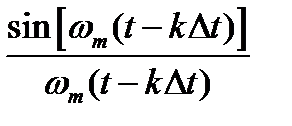 . Знаки закрепления (заморозки) $ расставлены таким образом, чтобы обеспечить правильную коррекцию формул при копировании их вниз и вправо. Таким образом формула вводится один раз и по ней вычисляются все точки всех функций-слагаемых ряда Найквиста-Котельникова.
. Знаки закрепления (заморозки) $ расставлены таким образом, чтобы обеспечить правильную коррекцию формул при копировании их вниз и вправо. Таким образом формула вводится один раз и по ней вычисляются все точки всех функций-слагаемых ряда Найквиста-Котельникова.
Скопируйте эту формулу вниз до строки 2000+64*Δtмшаг (в данном примере 2000+64*20=3280) и вправо до последнего 64-го столбца CL.
Проверьте правильность полученных результатов. Признаком правильности является равенство нулю (или очень малые числа) Z2000-CL2000, кроме клетки Z2000, в которой должно быть значение первого отсчета из клетки Z1999. В строке с номером 2000+шаг должно быть то же, что в строке 2000, но ненулевое значение должно быть уже во втором столбце (АА) и это значение должно совпадать со вторым отсчетом. И так в остальных строках с номерами 2000+шаг*номер отсчета.
Теперь для вычисления восстановленной по отсчетам функции x(t), нужно просуммировать столбцы-члены ряда вдоль строк (по горизонтали) и вычислить ошибку восстановления. Для этого введите данные согласно рис. 42.
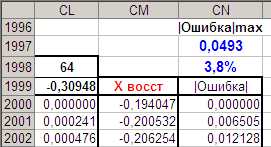
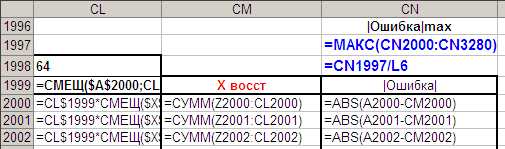
Рис. 42. Данные для вычисления суммы ряда и ошибки воспроизведения.
Формулы из клеток СМ2000 и CN2000 нужно копировать до конца суммируемых столбцов Z-CL.
Далее для визуальной оценки качества восстановления строим графики исходного и восстановленного сигналов. Графики строятся с использованием данных из столбца А (исходный сигнал) и столбца СМ (восстановленный сигнал, рис. 43). В данном примере для графика была взята первая тысяча отсчетов (с 2000 по 3000 строку).
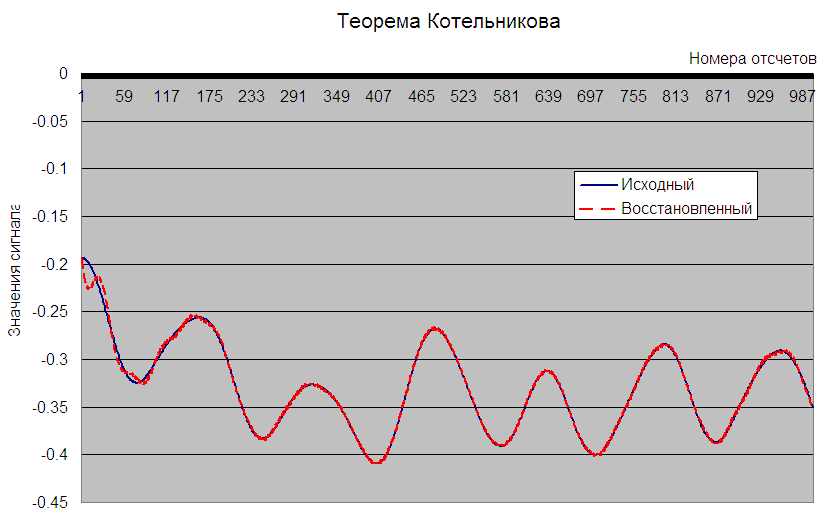
Рис. 43. Пример графика исходного сигнала и восстановленного с помощью ряда Найквиста-Котельникова сигнала.
Отличия в графиках исходного и восстановленного сигналов объясняется приближенным характером выполненных нами вычислений.
В качестве вывода можно отметить, что использование ряда Найквиста-Котельникова позволяет использовать наименьшее число отсчетов при наивысшей, почти абсолютной точности. Размеры шагов дискретизации и максимальной погрешности в зависимости от способа воспроизведения для данного варианта приведены в таблице 1.
Таблица 1.
Размеры шагов дискретизации и максимальной погрешности в зависимости от способа воспроизведения
| Полином Лагранжа 0 порядка | Полином Лагранжа 1 порядка | Ряд Найквиста-Котельникова | |
| Шаг дискретизации (в мшагах) | |||
| Погрешность (абсолютная и относительная | 0,0854 (6,6%) | 0,112 (8,6%) | 0,0493 (3,8%) |
Однако «платой» за это преимущество является высокая сложность вычисления ряда Найквиста-Котельникова.
В качестве задания обдумайте причину, по которой наибольшие ошибки оказались в начале восстановленного отрезка сигнала. Ответ ищите, используя иллюстрацию к порядку вычисления ряда Найквиста-Котельникова.
Результаты работы
В результате выполнения работы должен быть представлен архивный файл следующего содержания:
1. Wav-файл с записью голоса автора работы;
2. txt-файлы.
3. Еxcel-файл с расчетами;
4. Word-документ с титульным листом (см. образец титульного листа), теоретически обоснованным описанием хода выполнения работы, ее результатами и выводами.
Все файлы нужно упаковать при помощи архиватора WinZip или WinRar в один архивный файл и сдать преподавателю на проверку.
После этого работа защищается. При успешной защите она считается успешно выполненной, о чем преподаватель делает отметку в журнале.
Защита заключается в обсуждении теории по теме работы и хода ее выполнения.
Литература
1. Мацканюк А. А. Теория информации и кодирования: Учеб. пособие для студентов вузов спец. 351400 «Прикладная информатика (по областям)». – Сочи: РИО СГУТиКД, 2003. – 198 с.: 51 рис., 11 табл. – библиогр: 13 назв.
2. Кэтермоул К. В. Принципы импульсно-кодовой модуляции. –М.:Связь, 1974. – 408 с.
3. Советов Б. Я. Теория информации. –Л.: Из-во ЛГУ, 1977. – 184 с.
Вопросы для самопроверки
1. Что понимается под дискретизацией непрерывного сигнала по времени? Какой вид представления (непрерывный, непрерывно-дискретный или дискретный) в итоге получается и почему?
2. Сформулируйте теорему Котельникова-Найквиста.
3. Расскажите о трудностях ее практического использования.
4. Как на результаты дискретизации влияет размер шага дискретизации?
5. Перечислите критерии точности восстановления исходного сигнала.
6. Опишите функции Лагранжа.
7. Опишите форму сигнала, восстановленного при помощи полиномов Лагранжа нулевого, первого и второго порядков.
8. Опишите связь размера шага квантования по времени с порядком полиномов Лагранжа и ошибкой восстановления исходной функции?
Дата добавления: 2021-04-21; просмотров: 1840;











