Упрощённый способ построения линейного кода. Определение числа добавочных разрядов m.

Существует большое количество кодов, обнаруживающих и корректирующих искажения (ошибки), возникающие в результате действия помех в канале связи.

Коррекция (исправление) ошибок – операция более сложная и не всегда нужная. Коррекция ошибок подразумевает сначала обнаружение ошибок. Коррекция не предполагает повторное обращение к источнику сообщения и осуществляется на основании свойств самого искаженного сообщения. Если же возможен повторный запрос сообщения выгоднее, поскольку требуется меньше ресурсов, запрашивать повторную передачу сообщения до тех пор, пока в нем не перестанут обнаруживаться искажения. В этом случае используются более простые коды только обнаруживающие, но не исправляющие ошибки. Такие коды используются при передаче информации в компьютерных сетях, т.е. при передаче информации на расстоянии.

Корректирующие коды распространены при передаче информации во времени, например при записи ее на носители с целью последующего хранения. Во время хранения информация может быть искажена, но повторное ее получение не всегда возможно.

В данной лабораторной работе рассматривается один из видов кода – блоковый код – код при использовании которого во время кодирования некоторому числу информационных (кодируемых) разрядов ставится соответствие блок символов вторичного алфавита, называемый кодовым словом.

Код рассматриваемый в данной работе относится также к классу разделимых. Это означает, что в кодовых словах этого коды можно выделить информационные и дополнительные разряды.

Еще важно отметить, что рассматриваемый код относится к классу линейных. Принадлежность кода к классу линейных означает, что все кодовые слова такого кода получаются в результате линейных операций над небольшим количеством особых кодовых слов, которые называются линейно-независимыми [1].

Ниже следует описание операций, которые выполняются чтобы построить и использовать линейный код.

Определение числа добавочных разрядов m.

Добавочные (дополнительные) разряды в кодовом слове присоединяются к информационным и служат для борьбы с искажениями кодовых слов, которые возникают вследстве действия помех.

Одновременно дополнительные разряды увеличивают длину кодового слова, что является платой за помехоустойчивость. Поэтому количество этих разрядок должно быть минимально необходимым, для обеспечения заданной помехоустойчивости.

Для определения числа добавочных разрядов можно воспользоваться формулой границы Хэмминга [1]:

.

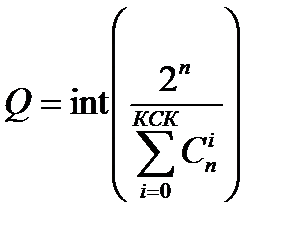При этом можно получить плотноупакованный код, т.е. код с минимальной при заданных параметрах кода длиной n кодового слова и, следовательно, избыточностью.

К задаваемым параметрам кода относятся: длина информационной последовательности k и корректирующая способность кода КСК[19].

При k информационных двоичных разрядах может передаваться 2^k кодовых слов. Если приравнять Q=2^k, то с учетом границы Хэмминга получаем: .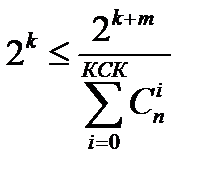

Если КСК=1, т.е. строится код, исправляющий максимум однократные ошибки, то ,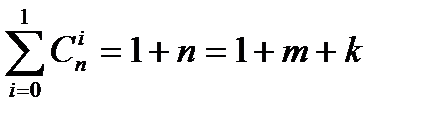

так как 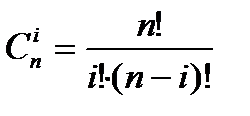и .

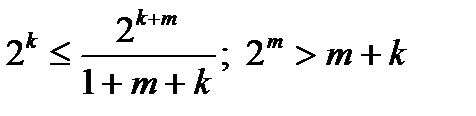С учетом последней формулы ищется (обычно путем простого переборв) наименьшее m при котором удовлетворяется это неравенство. Наименьшее потому, что при этом достигается наименьшая избыточность.

Пример: k=7, тогда путем простого перебора легко найти, что m=4.

Построение образующей матрицы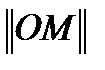

Линейные коды обладают следующим свойством: из всего множества 2^k разрешенных кодовых слов можно выделить подмножества из k слов, обладающих свойством линейной независимости.

Линейная независимость означает, что никакое из слов, входящих в подмножество линейно-независимых кодовых слов, нельзя получить путем суммирования (с помощью линейного выражения) любых других слов, входящих в это подмножество.

В то же время любое другое из разрешенных кодовых слов можно получить путем суммирования определенных линейно-независимых слов.

Таким образом, построение кодовых комбинаций линейного кода связано с линейными операциями. Для выполнения таких операций удобно пользоваться хорошо разработанным аппаратом матричных вычислений.

Для образования кодовых слов по информационной последовательности (кодирования) используют матрицу, называющуюся образующей.

Образующая матрица (ОМ) получается путем записи в столбец k линейно-независимых кодовых слов.

Обозначим кодируемую информационную последовательность X и будем записывать ее в виде матрицы-строки 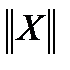размерностью 1*k, например: 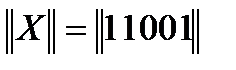, где k=5 .

Один из способов построения образующей матрицы следующий:

Она строится из единичной матрицы ||I|| размерностью k*k и приписанной к ней справа матрицы добавочных (избыточных) разрядов ||МДР|| размерности k*m:

||ОМ_k*n|| = ||I_k*k МДР_k*m||,

где при k=4 .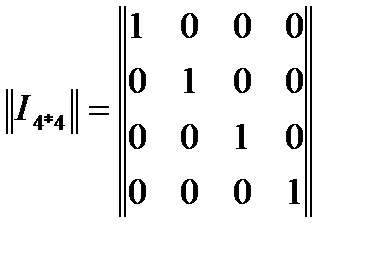

Такая структура ОМ обеспечивает получение разделимого систематического кода, т.е. кода, кодовые слова которого состоят из информационной последовательности и дополнительных разрядов, а дополнительные разряды образуются путем линейных операций над информационными.

Порядок построения матрицы МДР будет рассмотрен ниже.