Пропускная способность непрерывного канала при наличии аддитивного шума
Рассмотрим следующую модель канала:
1. Канал способен пропускать колебания с частотами ниже Fm.
2. В канале действует помеха n(t), имеющая нормальный (гаусcовский) закон распределения с нулевым средним значением.
3. Помеха n(t) статистически не связана с полезным сигналом x(t).
4. Помеха аддитивна, т.е. сигнал y(t) на выходе канала описывается формулой y(t) = x(t) + n(t), где x(t) – сигнал на входе канала.
5. Мощность Px полезного сигнала x(t) ограничена.
Ограниченность полосы пропускания канала приводит к ограниченности спектра выходного сигнала y(t). Поэтому согласно теореме Котельникова без потери информации сигналы x(t), y(t) и n(t) можно представить в виде ряда независимых отсчетов, взятых с шагом 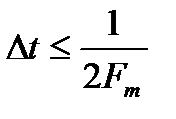 .
.
Как было доказано ранее количество информации I, приходящейся на один отсчет, равно: I = H(x) - H(x/y) = H(y) – H(y/x) .
Ранее нами было показано, что энтропия H(y) непрерывной случайной величины y находится по формуле:
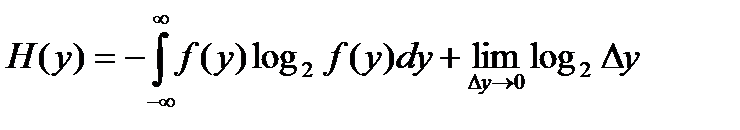 .
.
Найдем H(y/x). Перейдем к дискретному представлению x и y с шагом 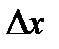 и
и 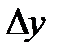 .
.
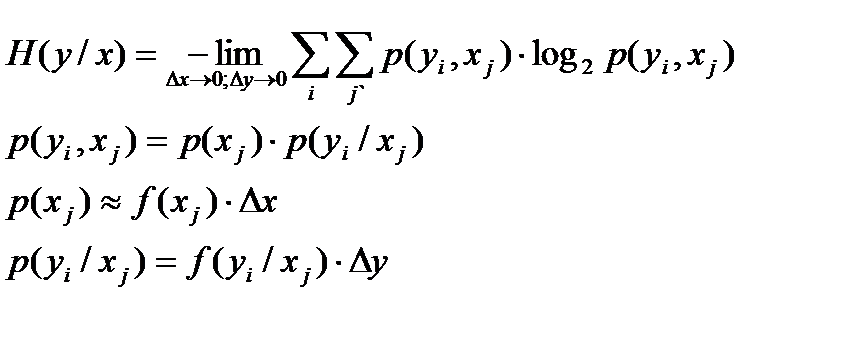
Найдем теперь дифференциальный закон f(y/x). Если x фиксирован, а y(t)=x(t)+n(t), то
f(y/x)=f(n-x).
График этой функции изображен на рис. 4.7.
Рис. 4.7. График функции f(y/x).
Поскольку Х фиксирован 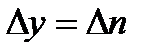 .
.
Произведем подстановки:
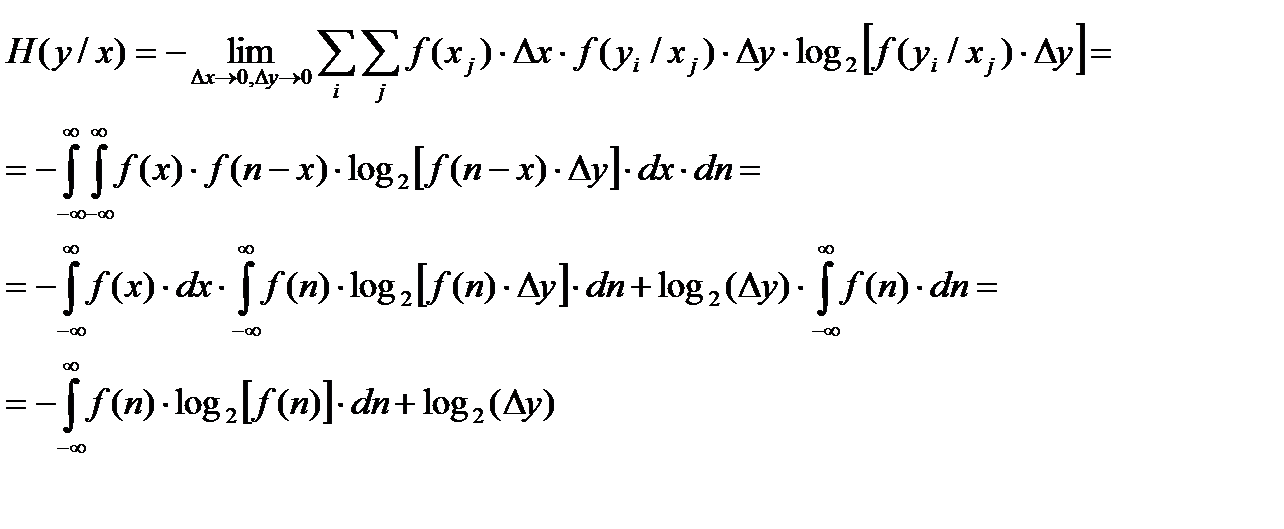
Подставив этот результат в формулу количества информации, получим:
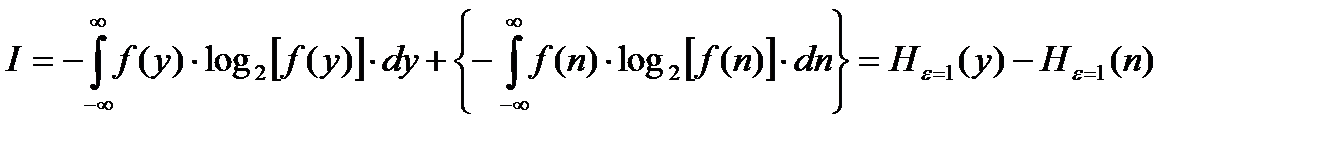 .
.
Скорость передачи информации:
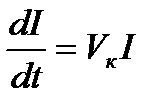 , где Vк=2Fm (по теореме Котельникова).
, где Vк=2Fm (по теореме Котельникова).
Для нахождения пропускной способности непрерывного канала связи с шумом следует максимизировать скорость передачи информации 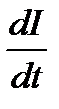 , варьируя параметрами передаваемого сигнала Х.
, варьируя параметрами передаваемого сигнала Х.
Vк – величина постоянная, связанная с параметром Fm канала.
I зависит от H(y).
Поcкольку x и n взаимно независимы, Dy = Dx + Dn, my = mx + mn = mx, так как mn = 0.
Ранее была выведена зависимость 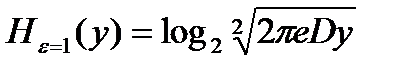 , из которой следует, что
, из которой следует, что 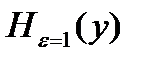 пропорциональна Dy.
пропорциональна Dy.
Отсюда следует, что 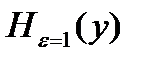 максимальна, когда максимальна дисперсия Dy.
максимальна, когда максимальна дисперсия Dy.
Но, поскольку Dy = Dx + Dn, Dy – максимальна, когда максимальна Dх.
Согласно условию, мощность Рх передаваемого сигнала Х ограничена сверху.
А, поскольку Рх = Dx + mx2, максимальное значение дисперсии Dx достигается при нулевом математическом ожидании mx=0. В это случае Рx=Dx.
Значит Py = Dy + my2 = Dy, так как my = mx + mn, а mx и mn = 0.
Ранее было доказано, что при ограничении мощности сигнала сверху его энтропия принимает максимальное значение, если он распределен по нормальному закону. Значит y должен иметь нормальный закон распределения.
А какой в этом случае закон распределения должен иметь входной сигнал х?
Поскольку y = x + n, а y и n имеют нормальные законы распределения, x и n не зависимы, согласно теории вероятностей x тоже должен иметь нормальный закон распределения.
Следовательно:
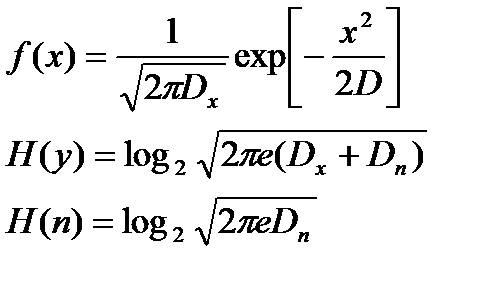
Отсюда:
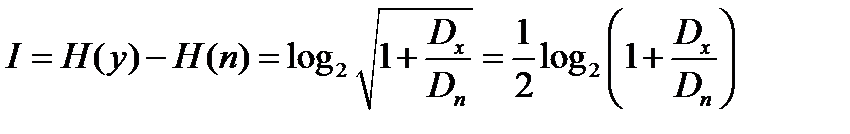 .
.
Поскольку mx и mn=0, Dx=Px, Dn=Pn,
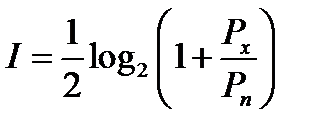 .
.
Отношение Px/Pn мощностей сигнала и шума называется отношением сигнал-шум.
В результате пропускную способность непрерывного канала связи с шумом можно записать в виде: 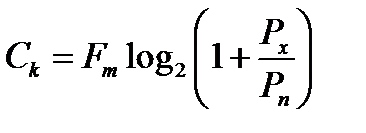 (4.6)
(4.6)
Таким образом, пропускная способность этого канала определяется максимальной частотой Fm пропускаемых через канал частот и отношением сигнал-шум. Пропускная способность этого типа канала тем выше, чем выше Fm и отношение сигнал-шум.
Формула (4.6) описывает наихудший в смысле величины пропускной способности случай. Если шум имеет негауссовский закон распределения или имеет коррелированные (зависимые) отсчеты, то пропускная способность канала возрастает.
Литература
1. Темников Ф. Е. и др. Теоретические основы информационной техники: Учеб. пособие для вузов. Ф. Е. Темников, В.А. Афонин, В.И. Дмитриев. – 2-е изд., перераб. и доп. –М.: Энергия, 1979. –512 с., ил.
2. Кузин Л. Т. Математические основы кибернетики. Том 1. Учеб. пособие. –М.: Энергия, 1973. –504 с.
3. Цымбал В.П. Теория информации и кодирования. −Киев: Вища школа; 1977. −288 с.
4. Кэтермоул К.В. Принципы импульсно-кодовой модуляции. −М.:Связь, 1974. −408 с.
5. Советов Б.Я. Теория ин формации. −Л.:Из-во ЛГУ, 1977. −184 с.
6. Яглом Л. М., Яглом И. М. Вероятность и информация. −М.:Наука, 1973. −512 с.
7. Шляпоберский В. И. Основы техники передачи дискретных сообщений. −М.: Связь, 1973. −480 с.
8. Липкин И. А. Основы статистической радиотехники, теории информации и кодирования. –М.:Советское радио. 1978. –240 с.
9. Галлагер Р. Теория информации и надежная связь. Пер с англ., под ред. М. С. Пинскера и Б. С. Цыбакова. –М.:Советское радио, 1974. −720 с.
10. Элементы теории передачи дискретной информации. Под ред. Л. П. Пуртова. −М.:Связь, 1972. −232 с.
Приложение 1. Таблица неприводимых полиномов
(По книге Темников Ф.Е. и др. Теоретические основы информационной техники. 3-е изд. –М.:Энергия, 1979. –512 с.)
| № п/п | Сте-пень | Полином | Двоичная последовательность |
| Х+1 | |||
| х2+х+1 | |||
| Х3+Х+1 | |||
| Х3+Х2+1 | |||
| Х4+Х+1 | |||
| Х4+Х8+1 | |||
| 7 | Х4+Х3+Х2+Х+1 | ||
| Х5+Х2+1 | |||
| Х5+Х3+1 | |||
| Х5+Х3+Х2+Х+1 | |||
| Х5+Х4+Х2+Х+1 | |||
| Х5+Х4+Х3+Х+1 | |||
| Х5+ Х4+Х3+Х2+l | |||
| х6+X1+1 | |||
| X6+X3+1 | |||
| X6+х4+х2+х+1 | |||
| х6+х4+X3+х+1 | |||
| х6+х5+1 | |||
| х6+х5+х2+х+1 | |||
| х6+х5+х3+х2+1 | |||
| X6+х5+х4+х+1 | |||
| х6+х5+х4+х2+1 | |||
| х7+х+1 | |||
| х7+х3+1 | |||
| х7+х3+х2+х+1 | |||
| X7+Х4+1 | |||
| X7+х4+х3+х2+1 | |||
| X7+X5+X2+X+1 | |||
| х7+х5+х3+х+1 | |||
| X7+X5+X4+X3+1 | |||
| X7+X5+X4+X3+X2+X+1 | |||
| X7+X6+11 | |||
| X7+X6+X3+X+1 | |||
| х7+х6+х4+х+1 | |||
| X7+X6+X5+X4+X2+1 | |||
| X7+X6+X5 +X2+1 | |||
| X7+X6+X5+X3+X2+X+1 | |||
| X7+X6+X5+X4+1 | |||
| X7+X6+X5+X4+X2+X+1 | |||
| X7+X6+X5+X4+X3+X2+1 | |||
| х8+х4+X3+х + 1 | |||
| X8+X4+X3+X2+1 | |||
| х8+х8+х3+х+1 | |||
| X8+X5+X3+X2+1 | |||
| Х8+Х5+Х4+Х3+1 | |||
| Х8+Х5+ х4+х3+х2+х+1 | |||
| X8+X6 +X3+X2+1 | |||
| X8+X6+X4+X3+X2+X+1 | |||
| X8+X6+X5 +X+1 | |||
| X8+X6+X5 +X2+1 | |||
| X8+X6+X5+X3+1 | |||
| X8+X6+X5+X4+1 | |||
| X8+X6+X5+X4+X2+X+1 | |||
| X8+X6+X5+X4+X3+X+1 | |||
| X8+X7 +X2+X+1 | |||
| х8+х7+х3+х+1 | |||
| х8+х7+х3+х2+1 | |||
| X8+X7+X4+X3+X2+X+1 | |||
| X8+X7+X5+X+1 | |||
| X8+X7+X5+X3+1 | |||
| х8+х7+х5+х4+1 | |||
| х8+х7+х5+х4+х3+х2+1 | |||
| х8+х7+х6+х+1 | |||
| X8+X7+X6+X3+X2+X+1 | |||
| х8+х7+х6+х4+х2+х+1 | |||
| X8+X7+X6+X4+X3+X2+1 | |||
| X8+X7+X6+X5+X2+X+1 | |||
| X8+X7+X6+X5+X4+X+1 | |||
| X8+X7+X6+X5+X4+X2+1 | |||
| X8+X7+X6+X5+X4+X3+1 | |||
| х9+х+1 | |||
| X9+ X4+1 | |||
| X9+X4+X2+X+1 | |||
| X9+X4+X3+X+1 | |||
| Х9+Х5+1 | |||
| X9+X5+X3+X2+1 | |||
| X9+X5+X4+X+1 | |||
| X9+X6+X3+X+1 | |||
| X9+X6+X4+X3+1 | |||
| х9+х6+х4+х3+х2+X+1 | |||
| X9+X6+X5+X2+1 | |||
| X9+X6+X5+X3+1 | |||
| X9+X6+X5+X3+X2+X+1 | |||
| X9+X6+X5+X4+X2+X+1 | |||
| X9+X6+X5+X4+X3+Х2+1 | |||
| X9+X7+X2+X+1 | |||
| Х9+Х7+Х4+Х2+1 | |||
| х9+х7+х4+х3+1 | |||
| Х9+Х7+Х5+Х+1 | |||
| х9+х7+х5+х2+1 | |||
| х9+х7+х5+х3+х2+х+1 | |||
| х9+х7+X5+х4+х2+х+1 | |||
| х9+х7+х5+х4+х3+х2+1 | |||
| х9+х7+х6+ х3+х2+х+1 | |||
| X9+X7+X6+X4+1 | |||
| X9+X7+X6+X4+X3+X+1 | |||
| х9+х7+х6+х5+х4+х2+1 | |||
| х9+х7+х6+х5+х4+х3+1 | 101111100J | ||
| х9+х8+1 | |||
| х9+х8+х4+х+1 | |||
| X9+X8+X4+X2+1 | |||
| X9+X8+X4+X3+X2+X+1 | |||
| х9+х8+х5+х+1 | |||
| X9+X8+X5+X4+1 | |||
| X9+X8+X5+X4+X3+X+1 | |||
| X9+X5+X6+X3+1 | |||
| Х9+х8+х6+Х3+х2+х+1 | |||
| X9+X8+X6+X4+X3+X+1 | |||
| х9+х8+х6+х5+1 | |||
| X9+X8+X6+X5+X3+X+1 | |||
| X9+X8+X6+X5+X3+Х2+1 | |||
| X9+X8+X6+X5+X4+X+1 |
Дата добавления: 2021-04-21; просмотров: 691;











