Типичные последовательности и их свойства

Будем рассматривать последовательности статистически независимых букв. Согласно закону больших чисел, наиболее вероятными будут последовательности длиной n, в которых при 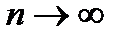количества N_i появлений букв отвечают зависимости N_i=p_i*n, где p_i – вероятность появления буквы i.

Последовательности, для которых выполняется равенство N_i=p_i*n, называются типичными.

Согласно закону больших чисел при росте n все большее число последовательностей становятся типичными, а в пределе, при 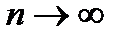, все последовательности становятся типичными.

Вероятность появления любой типичной последовательности вычисляется по одной и той же формуле:

,

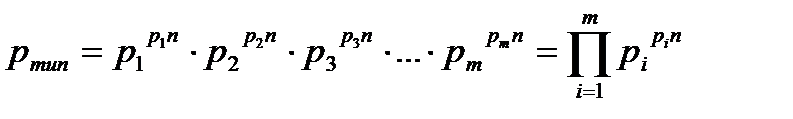где m – число букв в алфавите (объем алфавита).

Ниже нам понадобится формула, связывающая среднюю энтропию H буквы сообщения и длину n сообщения с количеством типичных последовательностей N_тип.

Поскольку с ростом n все последовательности становятся типичными, то сумма вероятностей их появления .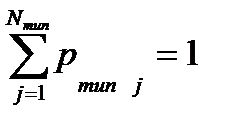

Учтем, кроме того, равенство этих вероятностей.

Отсюда находим энтропию H_тип типичной последовательности:

H_тип=-log₂(1/Nтип) = log₂N_тип .

Если H – энтропия буквы сообщения, то энтропия типичной последовательности Н_тип = n*H = log₂Nтип.

Отсюда N_тип = 2^nH .

Теперь мы готовы к восприятию основной теоремы Шеннона для дискретного канала с шумом.