Основная теорема Шеннона для дискретного канала с шумом

Формулировка

Для дискретного канала в шумом существует такой способ кодирования, при котором может быть обеспечена безошибочная передача все информации, поступающей от источника сообщений, если только пропускная способность канала превышает производительность источника сообщений, т.е. если выполняется условие:

V_{к max} [ log₂m – H(B/B’)] > V_и * H(A),(4.1)

где H(A) – энтропия источника.

Здесь обозначения соответствуют схеме, изображенной на рис. 4.6.

В – символы на входе, а В’ – на выходе канала; Vи и Vк – скорость поступления символов от источника на вход кодирующего устройства и с выхода кодирующего устройства на вход линии связи.

4.6. Схема системы передачи информации через дискретный канал связи с помехами и сопутствующие обозначения.

Доказательство

Согласно полученной ранее формуле, число типичных последовательностей длительностью Т равно:

N_тип(А) = 2^Vи*T*H(A) (4.2)

Максимально возможное число различных последовательностей на выходе кодера, которое сможет иметь ту же длительность, Т равна:

N(B) = m^Vк*T,

где m – объем вторичного алфавита.

Эту формулу можно записать также в виде:

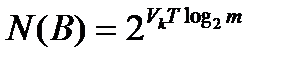(4.3)

Предположим, что условие теоремы V_к [ log₂m – H(B/B’)] > V_и * H(A) выполняется. Тогда, поскольку H(B/B’)>0, неравенство условия теоремы только усилится, если его записать в виде: V_к log₂m > V_и * H(A).

Домножим левую и правую части неравенства на Т и сделаем их показателями двойки:

.

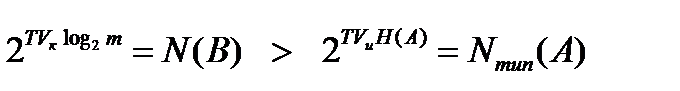Таким образом, возможное число последовательностей длительностью Т на выходе кодера больше числа типичных последовательностей той же длительности, которое может выдать источник.

Если установить однозначное соответствие между последовательностями на выходе кодера с последовательностями на входе, остаются последовательности, которые не могут использоваться для кодирования, т.е. запрещенные кодовые слова. Если все же такая последовательность получается с выхода канала связи – это верный признак ошибки.

Каждому способу кодирования будет соответствовать определенный вариант установки соответствия между каждой из множества типичных последовательностей, генерируемых источником и кодовым словом, взятым из множества разрешенных кодовых слов N(B).

Требуется теперь доказать, что среди всех возможных способов установки этого соответствия существует такой, который обеспечивает однозначную идентификацию любого принятого кодового слова, даже если оно получилось в результате искажения помехой передаваемого слова.

Для доказательства найдем вероятность правильного приема, усредненную по всем возможным способам кодирования, т.е. установки соответствия между принятым и возможно искаженным кодовым словом и закодированной информационной последовательностью.

По условной энтропии H(B/B’) можно найти количество возможных типичных последовательностей на входе канала, которые после искажения в нем могли бы дать определенную последовательность на выходе канала:

N_тип(B/B’) = 2^{T Vк H(B/B’) .} (4.4)

Вывод аналогичен сделанному ранее при исследовании свойств типичных последовательностей. Только в данном случае энтропия символа на выходе канала – функция того, какой символ получен на входе канала – H(B/B’).

Правильный прием возможен только тогда, когда на [N_тип(B/B’)-1] не разрешенных кодовых слов приходится одно разрешенное, т.е. число возможных кодовых слов вообще должно быть в N_тип(B/B’) раз больше числа типичных N_тип(A) последовательностей, которые может выдать источник.

Предположим теперь, что соответствия между типичными последовательностями, выдаваемыми источником, и кодовыми словами устанавливаются равновероятно. Тогда вероятность p_разр того, что определенное кодовое слово среди N_тип(А) является разрешенным, равна: p_разр=N_тип(А)/N(B) (кодируются только типичные последовательности).

Соответственно, вероятность того, что кодовое слово является запрещенным равна 1- p_разр= 1 - N_тип(А)/N(B).

Правильное декодирование возможно только тогда, если среди N_тип(B/B’) кодовых слов только одно выбрано в качестве разрешенного.

Вероятность этого равна:

.

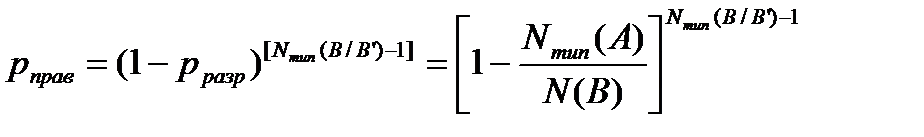Так как основание степени 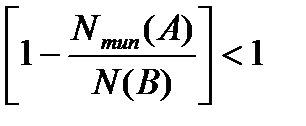, то, увеличивая показатель степени с N_тип(B/B’)-1 до N_тип(B/B’), получим неравенство:

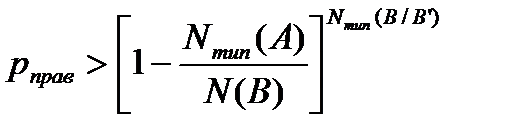. (4.5)

Разложим правую часть этого неравенства в ряд по степеням 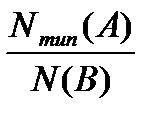(ряд Тэйлора[15]):

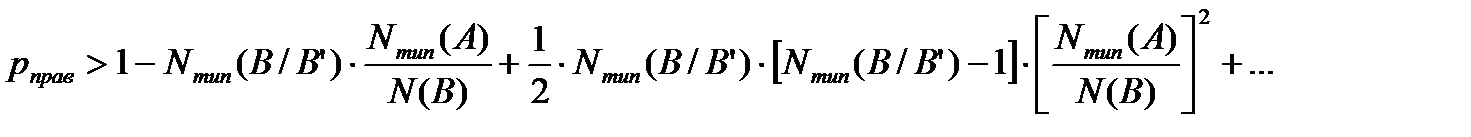
Поскольку 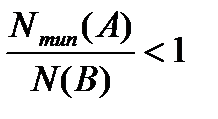и члены ряда по абсолютной величине убывают, неравенство (5) только усиливается, если отбросить все члены ряда выше первого порядка:

.

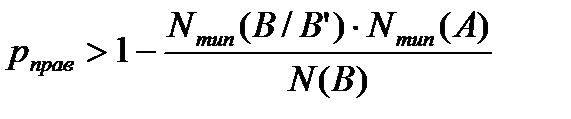Подставив в это выражение выражения (2), (3), (4), получим:

,

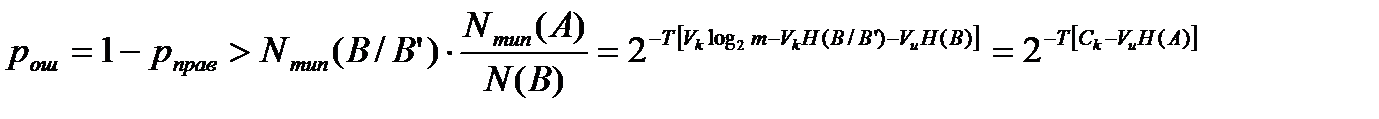где С_k =V_k*log₂m-V_k*H(B/B’) – пропускная способность канала связи с учетом потерь информации в результате действия помех (шума).

Заметим, что, если C_k > V_и*H(A) (условие теоремы Шеннона), с ростом Т вероятность ошибки Р_ош стремится к 0.

Помимо ошибки, возможной при приеме типичных последовательностей, вероятность которой определяется последней формулой, возможны ошибки за счет появления на выходе источника нетипичных последовательностей, кодирование которых вообще не предусматривается описанной процедурой. При вероятностях появления нетипичной последовательности 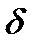и типичной суммарная вероятность ошибочной передачи равна: .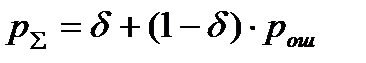

При 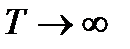, как было показано ранее, .

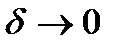Если С_k-V_иH(A) > 0 (т.е. при условии выполнения теоремы Шеннона), то пр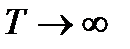и и суммарная ошибка .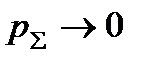

Поскольку среди всех вариантов кодирования обязательно существует хотя бы один, для которого вероятность ошибки не превышает среднего по всем вариантам кодирования значения 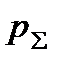, теорему Шеннона можно считать доказанной.