Обсуждение основной теоремы Шеннона для канала с шумом

Теорема Шеннона для канала с шумом не указывает на конкретный способ кодирования, обеспечивающий достоверную передачу информации со скоростью, сколь угодно близкой с пропускной способности канала связи. Она лишь доказывает принципиальную возможность существования такого кода. Однако из нее следует важный практический вывод: увеличения достоверности передачи информации возможно только при увеличении длины кодируемых информационных последовательностей и, следовательно, увеличении длины кодовых слов.

Кроме того, анализируя выведенную выше формулу вероятности ошибки

,

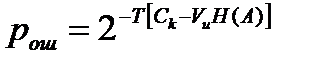приходим к выводу: чем выше запас по пропускной способности C_k-V_иH(A) имеет канал связи, тем вероятность ошибки ниже.

Таким образом, существует возможность размена эффективности использования канала на достоверность передачи информации, что иногда и делается на практике.

Теорема Шеннона имеет огромное значение для становления правильных воззрений на принципиальные возможности передачи информации. До Шеннона считалось, что сколь угодно малую вероятность ошибки можно получить лишь при стремлении скорости передачи информации к нулю.

Шеннон же своей теоремой показал, что путем введения в передаваемое сообщение избыточности, превышающей потерю информации в канале равную H(B/B’), в принципе можно добиться достоверной передачи информации через этот канал.

Действительно, энтропия H(B) входного закодированного сообщения, согласно теореме Шеннона, должна быть:

.

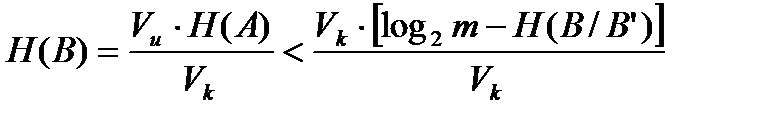Отсюда следует, что избыточность сообщения В на входе канала связи (закодированного, но еще не искаженного помехами) равна:

D_абс = H_max – H(B) = log₂m – log₂m + H(B/B’) = H(B/B’) .

Для наглядного пояснения роли теоремы Шеннона прибегнем к следующему сравнению. Пусть имеется трубопровод (аналог канала связи) для доставки некоторого жидкого продукта (аналог передаваемой информации), поступающего от источника этого продукта. Важнейшей характеристикой подобного трубопровода является его пропускная способность, т.е. максимальное количество жидкости, которое может перекачиваться через него в единицу времени. Еще одной важной характеристикой трубопровода являются потери перекачиваемого продукта из-за утечек (аналог искажения информации вследствие действия шума).

Можно теперь представить, какой эффект произвело бы утверждение, что существует такой способ введения примеси (избыточности) в продукт до его перекачки через трубопровод с утечкой и удаления этой примеси из перекачанного через трубопровод продукта, в результате чего после перекачки весь полезный продукт сохраняется, а в процессе перекачки из-за утечки теряется только примесь.

Именно такой смысл имеет вышеизложенная теорема применительно к задаче передачи информации через канал с шумом.