Шаг 4. Находим среднюю энтропию, приходящуюся на 1 букву сообщения.

<52 53 545556 57 58 >

Как описано в теоретическом введении, средняя энтропия находится по формулам 1 и 2. В обоих случаях нужно найти вероятности появления букв или двухбуквенных комбинаций..

Вероятности можно найти приближенно, исследуя частоты.

Для получения по этим частотам приближенных значений (оценок) вероятностей появления букв в тексте нужно сложить все частоты учитываемых букв и поделить частоту появления каждой буквы на эту сумму. Это удобно сделать в дополнительном столбце, расположенном рядом со столбцом, содержащим частоты появлений отобранных символов - букв.

До расчета средней энтропии появления букв без учета статистических связей между ними нужно найти слагаемые в формуле суммы 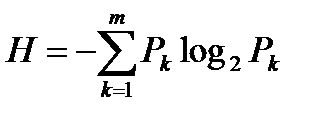и, наконец, просуммировать их. Это довольно просто. Напомним только, что log₂X = lnX / ln2. Можно также воспользоваться имеющейся в Excel стандартной функцией log(1 аргумент, 2 аргумент). Здесь 1 аргумент – аргумент логарияма, 2 аргумент – основание логарифма, в данном случае 2.

Для расчета оценок вероятностей появления двухбуквенных комбинаций нужно повторить вышеописанные шаги обработки информации, начиная с преобразования символов в числа. В отличие от предыдущего в этом случае в числа нужно преобразовывать не отдельные символы, а комбинации из двух символов. Здесь нужно выбрать такой способ преобразования, чтобы каждой комбинации их двух символов было поставлено в соответствие определенное число, связанное именно с этой комбинацией.

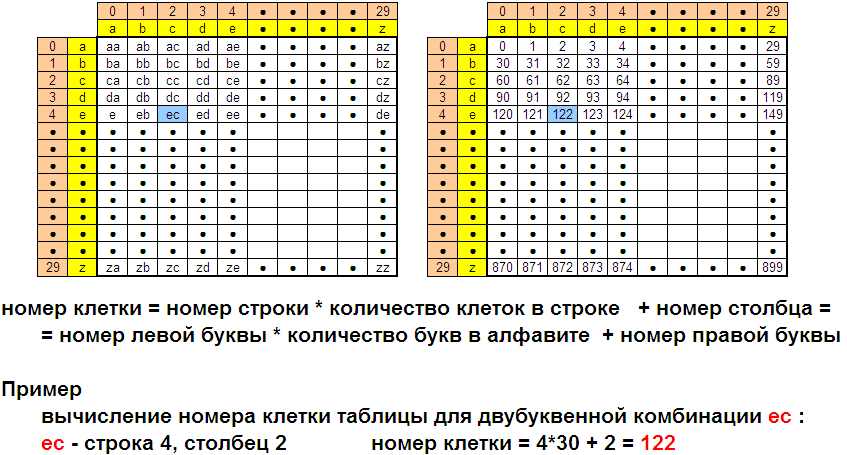
Этого можно достичь, если считать буквы символами некоторой системы счисления, а двухбуквенные комбинации – двухразрядными числами, записанными в этой системе счисления. Основание системы счисления в этом случае будет равно числу букв в алфавите. например, большинство языков, использующих латиницу, имеют в алфавите всего 26 букв. Следовательно, двухбуквенные комбинации на этом языке можно считать двухразрядными 26-ричными числами. Известно, что общее число чисел, которое может быть записано в общем случае n-разрядным m-ичным числом равно mⁿ. В данном случае это число = 26² = 676.

Сразу оговоримся, что, если в алфавите более 255 букв (языки с иероглифической письменностью), возможностей табличного процессора Excel для расчета энтропии с учетом статистической зависимости между соседними буквами становятся недостаточными и в этом случае расчет энтропии мы производить не будем.

Если же учитываемых букв в алфавите меньше 256, каждую встреченную в тексте двухбуквенную комбинацию, которую мы теперь понимаем как число, записанное в недесятичной системе счисления, нужно заменить на соответствующее число, записанное в десятичной системе счисления.

Для этого используется формула, которая студентами должна быть известна еще из школьного курса информатики:

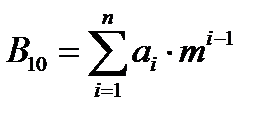, (3)

где В₁₀ – результат преобразования исходного m-ичного числа А_m в десятичную систему счисления;

n – количество разрядов исходного числа, записанного в m-ичной системе счисления;

m – основание системы счисления;

a_i – разряды числа А_m = a_na₍_n_-1)….a₁ , записанные в виде десятичных чисел.

В нашем случае n=2, а m= 26 (в некоторых вариантах латиницы).

Из вышесказанного следует такой план действий:

· отдельные буквы преобразуем не в коды, а номера их следования в алфавите (номера будем отсчитываю не с 1, а с 0):

· для образования уникального для каждой двухбуквенной комбинации числа используем формулу 3.

Преобразование символа в его номер в алфавите удобно выполнять при помощи функции ВПР.

Напомним, что функция ВПР предназначена для поиска одних значений по другим. Она имеет 3 аргумента: первый – для указания искомой величины, второй – для указания местоположения таблицы, в первом столбце которой ищется искомая величина; третий – для указания столбца из клетки которого выбирается результат поиска. Более подробное описание функции ВПР смотрите в приложении 3.

Создадим еще один рабочий лист (Лист4). В нем на месте, под которым на исходном листе нет символов, создадим таблицу, в первом столбце которого будут находиться учитываемые символы алфавита, а справа во втором столбце – их номера по порядку, начиная с номера 0.

Теперь можно заняться преобразованием символов в их номера в алфавите. Для этого можно использовать, например, такую формулу:

A1 ← = если ( еошибка ( впр (………!A1; $BR$1 : $BS$26; 2 ) ); -1; впр (………!A1; $BR$1:$BS$26 ; 2 ) )

Функция еошибка в этой формуле предназначена для проверки возможности найти в таблице букву, а по ней ее номер. Если аргумент функции еошибка - функция впр - букву в таблице не находит, она принимает значение ошибки, и тогда функция еошибка принимает логическое значение Истина. В этой ситуации функция если становится равной своему второму аргументу, т.е. -1. Ранее мы условились считать значение -1 признаком неверных данных. Если же функция еошибка равна логическому значению Ложь, это означает что ее аргумент – функция впр - нашла букву в таблице, что приводит к приданию функции если значения ее третьего аргумента, т.е. впр, которая в этом случае равна номеру буквы в алфавите.

Эту формулу надо размножить на все клетки, которые соответствуют клеткам с буквами исходного листа.

В результате мы только получаем вместо букв их номера и -1 там, где находятся пустые клетки или другие неучитываемые символы. Теперь можно приступить к образованию из двух соседних букв, понимаемых как 2 разряда 26-тиричного (в данном примере) числа, соответствующего ему десятичного числа. Для этого нужно воспользоваться формулой 3.

Но прежде, для размещения этих числе создадим еще один новый рабочий лист (Лист5).

Расчетная формула, преобразующая двухбуквенную комбинацию в число, может быть следующей:

А1 ← =ЕСЛИ ( ИЛИ ( Лист4!A1 < 0; Лист4!B1 < 0); -1; Лист4!A1 * 26 + Лист4!B1 )

Здесь функция если предназначена для проверки того, что в соседних клетках находятся номера букв (признаком небуквы является число -1). Условие проверки сформировано при помощи функции или.

Эту формулу нужно размножить на ту же область, что занимают буквы в исходном листе, кроме последнего его столбца, т.к. комбинации из двух букв берутся из двух соседних столбцов.

Последующие действия почти совпадают с аналогичными действиями, ранее выполненными при расчете энтропии в случае неучена статистических связей между буквами.

Отличия заключаются в следующем:

· Интервал карманов должен содержать числа от -1 до m² , где m – число учитываемых букв алфавита (в нашем примере m = 26, значит m₂=676).

· После нахождения при помощи инструмента Гистограмма частот появления двухбуквенных комбинаций, некоторые частоты окажутся равными нулю. Из можно не подавлять фильтром, однако при расчете слагаемых p_ilog₂p_i нужно использовать функцию если для принудительного приравнивания таких слагаемых к 0, поскольку напрямую такие выражения Excel вычислить не может.

· Полученная энтропия будет относиться не к одной, а к двум буквам. Для приведения же результат к одной букве следует поделить его на 2.

Шаг 5. Находим абсолютную и относительную избыточности источника сообщений на заданных языках, сравнить эти языки по степени избыточности написанных на них текстов без учета и с учетом статистических связей между соседними буквами если размер алфавита языка позволил его произвести.

Согласно [1], различают 2 вида избыточности – абсолютную и относительную.

Абсолютная избыточность D_abs находится в виде разности между максимально возможной H_max и действительной энтропией H сообщения:

D_abs = H_max - H

Относительная избыточность D находится как отношение абсолютной избыточности D_abs к максимальной энтропии H_max:

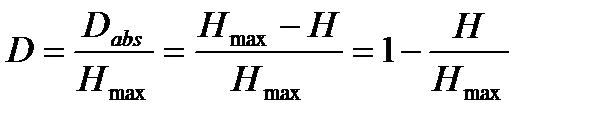
Максимального значения энтропия достигает при равной вероятности всех букв сообщения.

Максимальная энтропия находится по формуле:

H_max = log₂m

Здесь m - количество учитываемых букв или двухбуквенных комбинаций.

Таблица с результатами вычисления должна содержать от 2 до 4 значений энтропий. Вам необходимо сравнить значения энтропий и по 2 значения избыточности для каждой энтропии. Нужно также по сведенным в таблицу данным сделать заключение о степени информативности исследованных языков, сравнивая их энтропии разных языков между собой и с учетом влияния статистической связи между буквами.

<52 53 545556 57 58 >

Дата добавления: 2021-04-21; просмотров: 641;