Пропускная способность дискретного канала связи с шумом

Исследуем теперь пропускную способность дискретного канала связи с шумом.

Существует большое количество математических моделей таких каналов. Простейшей из них является канал с независимой от передаваемой информации помехой, имеющей независимые во времени значения. Последнее означает, что влияние помехи на различные буквы передаваемого сообщения не зависят друг от друга. Будем рассматривать канал без стирания с алфавитом объема m (не двоичный симметричный канал ДСМК, так как m не равно 2).

Если в канале без помех среднее количество информации, получаемой с выхода канала в единицу времени, соответствует среднему количеству информации, содержащейся во входном сообщении той же длительности, то в канале связи с шумом это соответствие нарушается. При наличии помехи скорость передачи информации через канал может быть меньше скорости ее поступления на его вход, так как часть информации за счет помех в канале может теряться.

Помехи нарушают взаимно-однозначное соответствие между символами на входе и выходе канала, что приводит к появлению на выходе канала остаточной неопределенности об информации, поступившей на вход канала.

Количество переданной информации при этом вычисляется согласно формуле Шеннона как разность между априорной и апостериорной энтропиями:

I = H_апр – Н_апост ,

,

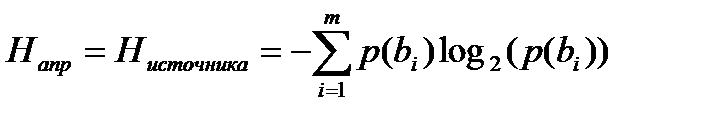где b_i – i-я буква из алфавита объемом m.

H_апост = Н(B/B’) – средняя условная энтропия 1 буквы на входе канала связи с шумом относительно 1 буквы, принятой на выходе канала связи. Найдем эту энтропию.

В результате искажения передаваемые буквы b_i превращаются в другие b_i’ из того же алфавита. Вероятность такого превращения можно описать графом, называемым канальной матрицей(рис. 4.5).

Рис. 4.5. Канальная матрица.

Каждому ребру этого графа соответствует условная вероятность p(b_i/b_j’) – вероятность того, что на вход канала поступал символ b_i при условии, что на выходе был получен символ b_j’ (выходные символы обозначаются со штрихом).

Неопределенность (энтропия) того, какой символ был на входе канала связи по символу полученному на выходе находится согласно определению энтропии по формуле: H(b_i/b_j’)=-log₂ p(b_i/b_j’).

Нас интересует средняя неопределенность независимо от сочетания входной и выходной буквы. Вероятность такого сочетания – совместная вероятность p(b_i,b_j’).

Использую совместную вероятность, среднюю условную энтропию получаем в виде:

.

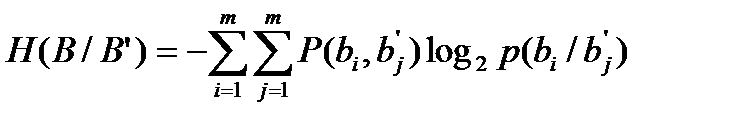Учитывая, что 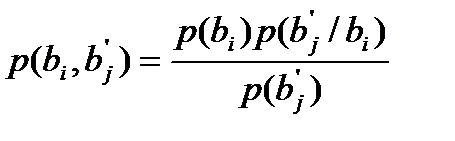(формула Байеса)

и

,

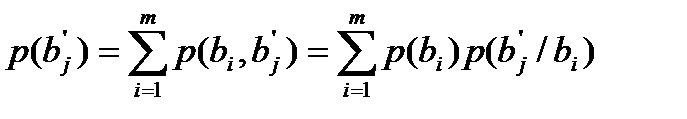получим:

.

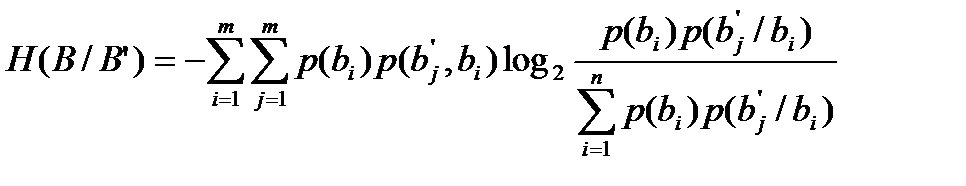Значение условной энтропии H(B/B’) характеризует потери информации в канале и названа К. Шенноном ненадежностью канала.

Из выведенной выше формулы следует, что ненадежность канала зависит от статистических характеристик входного сообщения В (вероятностей р(b_i)), а также от искажений, описываемых условными вероятностями p(b_j’/b_i).

Подставив теперь выражения для априорной и апостериорной энтропии в формулу среднего количества информации на символ сообщения, получим:

.

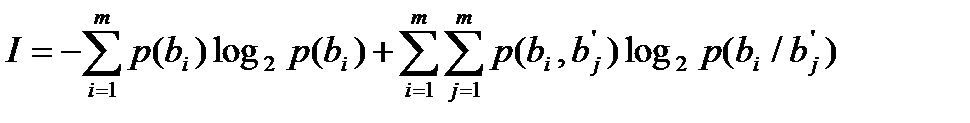После преобразований получим:

.

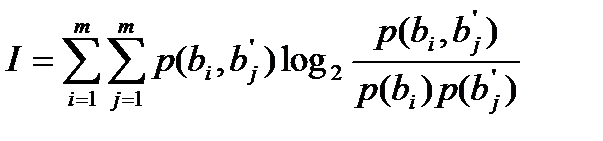Заметим, что эта формула симметрична относительно b_i и b_i’, поэтому

I = H(B) – H(B/B’) = H(B’) – H(B’/B) ,

т.е., во-первых:

среднее количество информации на символ равно разности энтропии на входе и неопределенности на выходе относительно входа;

во-вторых:

оно равно разности неопределенности (энтропии) на выходе и неопределенности того, что получено на выходе, если известно, что было передано на входе канала.

Пропускная способность получается путем максимизации скорости передачи информации по каналу связи путем подбора вероятностей p(b_i).

C_к = V_{к max} * I = V_{к max}*[H(B) – H(B/B’)] .

Вообще и уменьшаемое H(B) и вычитаемое H(B/B’) в этой формуле зависят от p(b_i), однако большинство авторов зависимостью вычитаемого H(B/B’) от p(b_i) ввиду его малости пренебрегают и учитывают зависимость С_к только от уменьшаемого H(B).

Известно, что энтропия H(B) максимальна при равенстве всех вероятностей p(b_i). Это равенство возможно только при условии p(b_i)=1/m. В результате получаем, что пропускная способность дискретного канала связи с шумом равна C_к = V_к [log₂m – H(B/B’)] .

Посмотрим теперь, как влияет шум на пропускную способность канала связи.

Ненадежность канала H(B/B’) будет минимальна и равна 0, если шума нет. Тогда символы на входе и выходе всегда совпадают. Это значит, что:

.

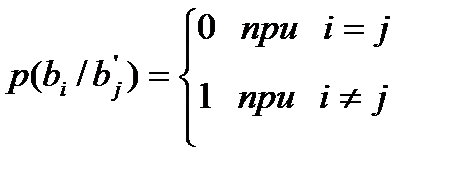В этом случае H(B/B’)=0, а пропускная способность С_{к max} совпадает с пропускной способностью канала связи без шума, что и следовало ожидать.

Если же шум настолько велик, что все символы на выходе могут появляться равновероятно не зависимо от того, какой символ подавался на вход канала связи, т.е. если p(b_i/b_j’)=1/m и p(b_j’)=1/m, то I=0.

Это несложно доказать.

.

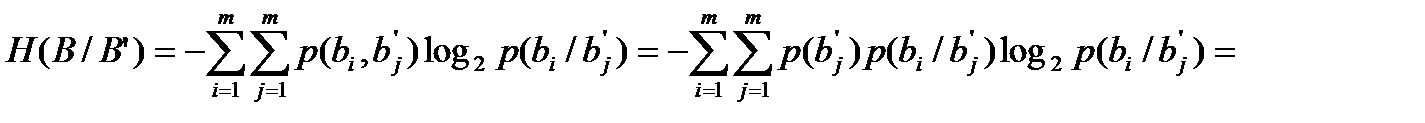
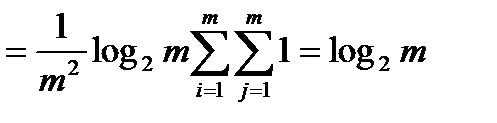А так как I=H(B)-H(B/B’), где H(B)=log₂m, то I=log₂m-log₂m=0.

Для доказательства очень важной теоремы, доказанной еще в 40-х годах 20 века Шенноном для дискретного канала с шумом, введем понятие типичных последовательностей и рассмотрим их свойства.