Направление выпуклости графика функции. Точки перегиба

График функции y = f(x)называется выпуклым вверх (выпуклым) на интервале (a; b) если в пределах этого интервала график функции y = f(x) лежит ниже любой своей касательной.

График функции y = f(x) называется выпуклым вниз (вогнутым) на интервале (a; b) если в пределах этого интервала график функции y = f(x) лежит выше любой своей касательной.

Точка графика функции y = f(x) M₀ (x₀; f(x₀))называется точкой перегиба графика, если при переходе x через x₀график меняет направление выпуклости.

Пусть функция y = f(x) дважды дифференцируема на интервале (a;b), тогда если в каждой точке этого интервала 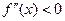, то график функции на (a; b) выпуклый вверх (выпуклый), а если 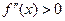, то график функции на (a; b) выпуклый вниз (вогнутый). Это достаточные условия выпуклости (вогнутости) графика.

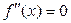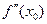Если точка M₀ (x₀; f(x₀))является точкой перегиба графика функции y=f(x), то или не существует – необходимое условие точки перегиба.

Точка x₀ области определения функции, в которой вторая производная функции обращается в ноль или не существует, называется критической точкой II рода.

Для того чтобы точка M₀ (x₀; f(x₀))графика функции y=f(x) была точкой перегиба, достаточно, чтобы существовала конечная 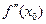в некоторой окрестности точки x₀ (за исключением, может быть, самой точки x₀) и чтобы 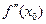меняла знак при переходе x через x₀.

Пример 1. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции .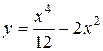

Решение.

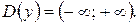
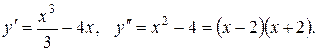
Находим критические точки II рода:

а) 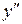не существует: ,

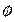б) 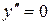при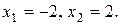

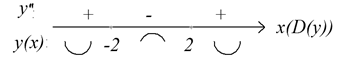
Вычислим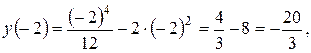

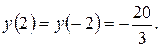
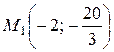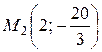Получим и − точки перегиба.

Ответ: 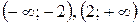– интервалы вогнутости, 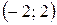− интервал выпуклост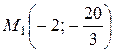и, и 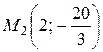− точки перегиба.

Пример 2. Найти интервал выпуклости, вогнутости и точки перегиба графика функции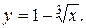

Решение.

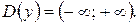
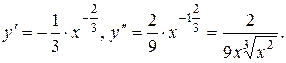
Находим критические точки II рода:

а) 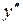не существует при ,

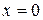б) :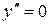

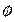
Вычислим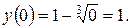

Получим 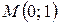− точка перегиба.

Ответ: 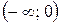− интервалы выпуклости, 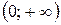− интервал вогнутости, 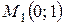− точка перегиба.