Магнитное поле тороида и соленоида.
Закон полного тока (1.5.10) часто используют для расчета индук-ции магнитного поля постоянного электрического тока. Для примера рассмотрим применение закона полного тока для расчета индукции магнитного поля соленоида и тороида.
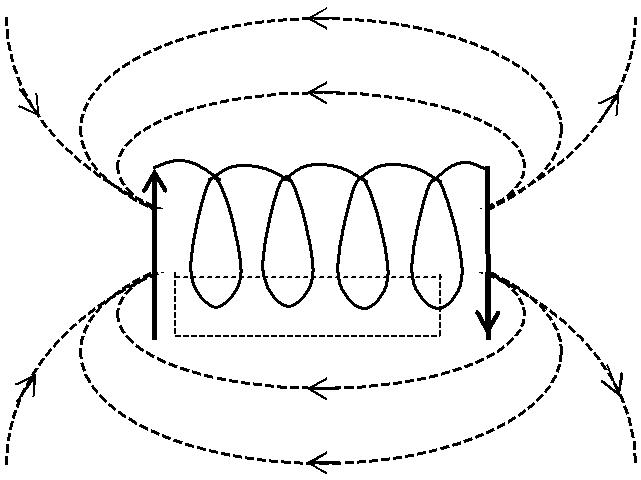
Соленоид–это катушка индуктивности в виде намотанного на ци-линдрическую поверхность изолированного проводника, по которому течет электрический ток. Рассмотрим соленоид длиной l, имеющей N витков. Длину соленоида считаем во много раз больше, чем диаметр его витков, то есть рассматриваемый соленоид бесконечно длинный. Внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым, и чем длиннее соленоид, тем меньше магнитная индукция вне его. Поэтому будем считать, что поле бесконечно длинного соле-ноида сосредоточено целиком внутри него.
Для нахождения магнитной индукции выберем замкнутый пря-моугольный контур ABCDA (рис. 1.6.1) Согласно теореме о цирку-
ляции вектора H:
| ∫ Hl dl = NI. | (1.6.1) |
ABCDA
D  A
A
C B
Рис. 1.6.1
Интеграл по ABCDA можно представить в виде интегралов по AB; BC; CD; DA.На участках AB и CD контур перпендикулярен линияммагнитной индукции и Hl = 0. На участке CB вне соленоида Н = 0, а на участке DA контур совпадает с линией магнитной индукции и циркуляция вектора H равна
| ∫ Hl dl = Hl = NI. | (1.6.2) |
| DA |
Из последнего уравнения получаем, что напряженность магнит-ного поля соленоида:
| NI | (1.6.3) | ||
| H = | l = nI , | ||
где n – число витков соленоида, приходящихся на единицу длины . Используя формулу (1.1.1), выражаем индукцию магнитного поля
соленоида:
| B =μμ0 | N | I =μμ0nI. | (1.6.4) | |
| l | ||||
Тороид–это кольцевая катушка с витками,намотанными на сер-дечник, имеющий форму тора, по которому течет электрический ток.
Пусть R1 и R2 соответственно внешний и внутренний радиусы се-чения тороида. Общее число витков тороида с током I равно N.
| Если r < R2, то контур не охватывает проводники | с током, |
| N | |
| ∑Ik = 0, и по закону полного тока | |
| i=1 | |
| ∫ Hdl cosα=2πrH =0⇒ H =0. | (1.6.5) |
| L |
Если r > R1, то контур охватывает 2N проводников с током I. По-ловина из них идет в одном направлении, а половина – в обратном на-правлении (рис. 1.6.2). Поэтому алгебраическая сумма токов во всех проводниках равна нулю, и поэтому
| 2 πrH = 0 ⇒ H = 0. | (1.6.6) |
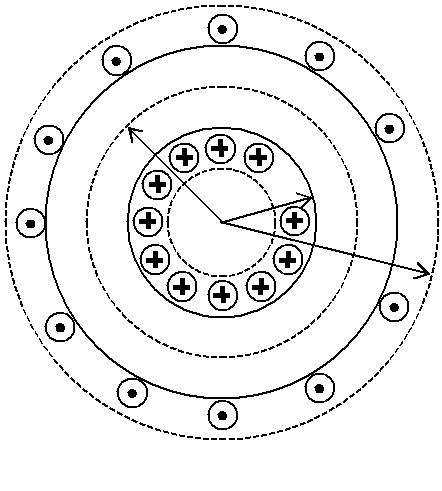
r
R2 
Рис. 1.6.2
R1 
Из полученного результата следует, что вне тороида магнитное поле отсутствует. Магнитное поле сосредоточено внутри объема (R2 ≤ r ≤ R1) тороида. Линии магнитной индукции в данном случае есть окружно-сти, центры которых расположены на оси тороида. В этом случае кон-тур радиуса r охватывает N проводников, токи в которых равны I и одинаково направлены. Поэтому по теореме о циркуляции
| ∫ Hl dl = Hl =2πrH = NI. | (1.6.7) | |||||
| L | ||||||
| Отсюда напряженность магнитного поля внутри тороида: | ||||||
| NI | (1.6.8) | |||||
| H = | 2 πr = nI , | |||||
где n – число витков тороида, приходящихся на единицу длины. Напряженность магнитного поля на осевой линии тороида равна:
| Hср = | NI | . | (1.6.9) | |
| 2πr | ||||
| ср |
Используя формулу (1.1.1), находим индукцию магнитного поля внутри тороида:
| B =μμ0 | NI | = μμ0nI. | (1.6.10) | |
| 2πr | ||||
Индукция магнитного поля на осевой линии тороида равна:
| B =μμ | NI | =μμ | nI. | (1.6.11) | ||
| 0 2πr | ||||||
| cp | ||||||
| cp |
Дата добавления: 2017-01-08; просмотров: 4418;











