Магнитное поле. Взаимодействие токов. Вектор магнит-ной индукции.
В пространстве, которое окружает электрические токи или по-стоянные магниты, возникает поле, называемое магнитным. На контур с током или магнитную стрелку, помещенные в магнитное поле, последнее оказывает ориентирующее действие. Все постоян-ные магниты обладают полюсами, которые носят название север-ный и южный. Одноименные полюсы взаимно отталкиваются, а разноименные – притягиваются.
Силовой характеристикой магнитного поля является вектор маг-
нитной индукции(или иначевектор индукции магнитного поля)
B.Определение и физический смысл вектора магнитной индукциибудут рассмотрены ниже.
B
Силовая линия
Рис. 1.1.1
B
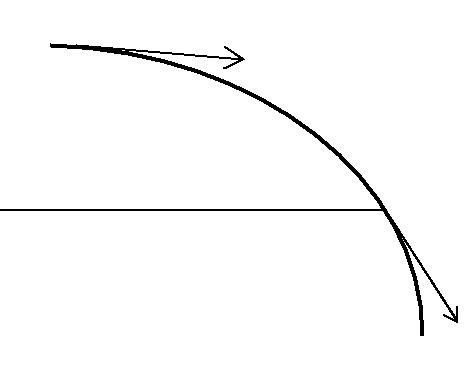
Графически (рис. 1.1.1) магнитное поле изображают с помощью
линий магнитной индукции(силовых линий) –линий,касательныек которым в каждой точке совпадают с направлением вектора маг-
нитной индукции.Линии магнитной индукции всегда замкнуты,вы-ходят из северного полюса и входят в южный полюс и охватывают проводники с током. Густота линий магнитной индукции пропорцио-нальна величине индукции магнитного поля.
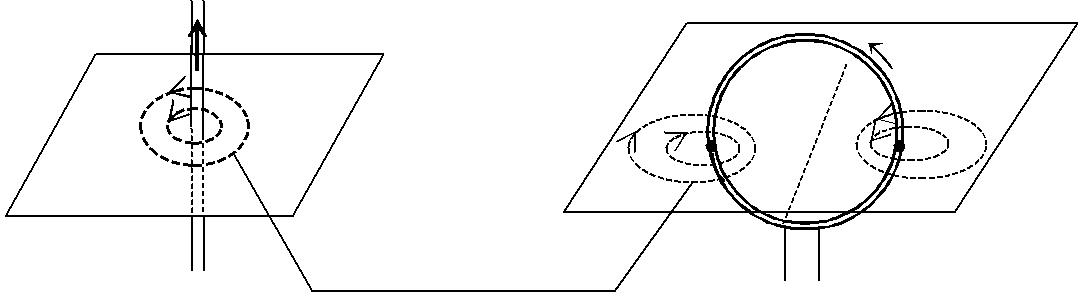
В качестве примера рассмотрим силовые линии прямого и круго-вого проводников с токами. В случае прямого тока линии индукции (рис. 1.1.2, а ) представляют собой концентрические окружности (с центрами на оси проводника), которые расположены в плоскостях, перпендикулярных току. При этом направление линий индукции удобно определять по правилу буравчика (или правилу правого винта)в основной формулировке:если направление поступатель-ного движения оси буравчика сопоставить с направлением прямого тока, то направление вращения его рукоятки укажет направление линий магнитной индукции.
I
I
Силовые линии
а б
Рис. 1.1.2
Силовые линии индукции кругового тока изображены на рис. 1.1.2, б, причем направление силовых линий также определяется по правилу буравчика.
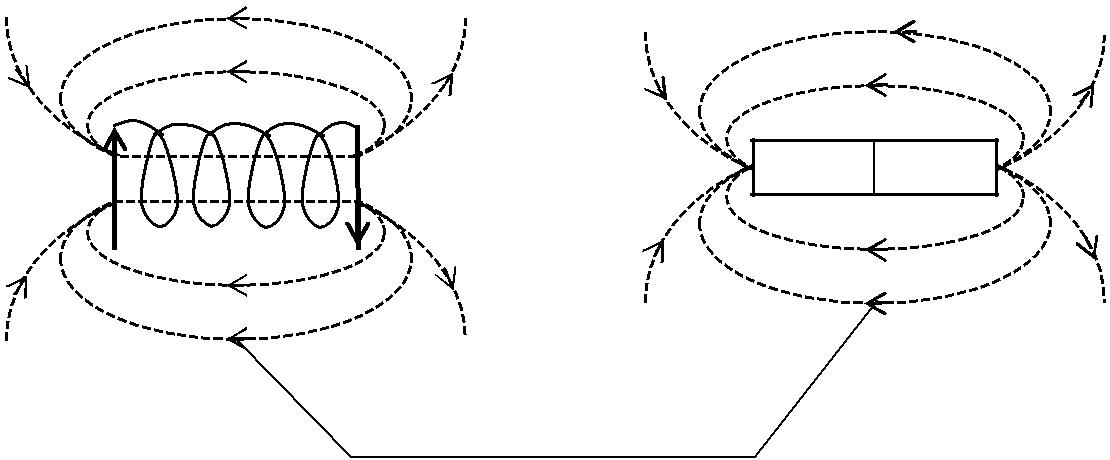
Линии индукции соленоида, который представляет собой систему одинаковых круговых токов, схематично изображены на рис. 1.1.3, а. Внутри соленоида, длина которого намного больше диаметра его вит-ков, магнитное поле является однородным, а прямые линии магнитной индукции направлены так, чтобы выполнялось правило буравчика
(неосновная формулировка): если рукоятку буравчика вращать по на-правлению тока в витках, то силовые линии будут направлены по движению оси буравчика.Все линии индукции на рисунке или замкну-ты, или имеют тенденцию замкнуться, если их продлить. Линии индук-ции соленоида очень схожи с линиями прямого (полосового) магнита (рис. 1.1.3, б), которые выходят из северного полюса N и входят в юж-ный полюс S. Кажется, что они разорваны в объеме магнита. Однако опыты и теоретические расчеты показали, что линии индукции и в этом случае замкнуты внутри магнита. В связи с тем, что магнитные поля соленоида и полосового постоянного магнита схожи друг с другом,
торцам соленоида часто приписывают полярность. Французский физик А. Амперу высказал гипотезу о том, что магнитные свойства постоян-ных магнитов обусловлены существующими в них микротоками . К настоящему времени эта гипотеза полностью обоснована и лежит в ос-нове современных представлений о магнитных свойствах вещества.
| S | N | S | N |
| I |
Силовые линии
а б
Рис. 1.1.3
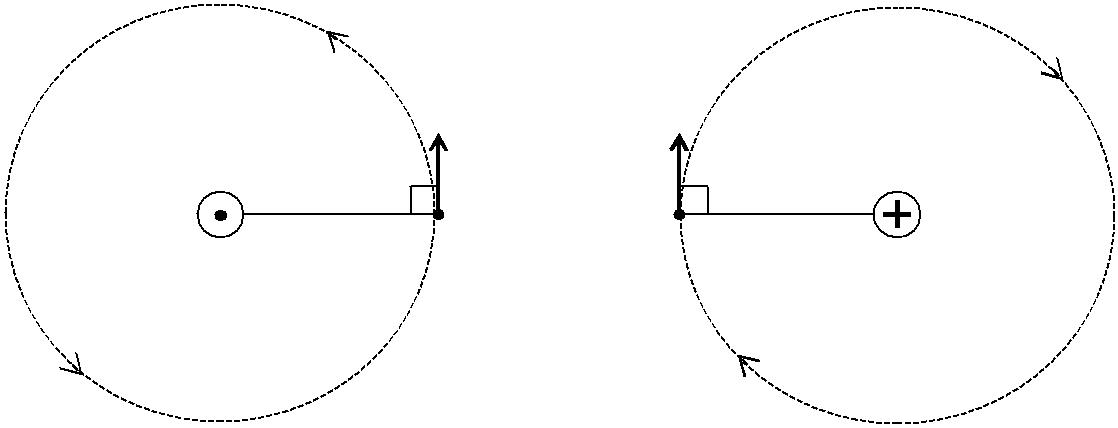
На рис. 1.1.4 приведены примеры использования правила правого винта в основной формулировке для определения направления векто-ра магнитного поля B, создаваемого токами I1 и I 2. На рисунке ток си-лой I1 ( ) – «ток к нам», а ток силой I2 (⊕) – «ток от нас».
| B1 | B2 | I2 | |
| I1 |
Рис. 1.1.4
Поскольку магнитное поле действует на проводник с током, то, на-пример, два параллельных гибких проводника с токами одинакового на-правления притягиваются, выгибаясь, как показано на рис. 1.1.5 штрихо-выми линиями. Противоположно направленные токи отталкиваются.
Вектор магнитной индукции характеризует результирующее маг-нитное поле, создаваемое всеми макро- и микротоками. Макроско-
пические токи−это электрические токи,протекающие по про-водникам в электрических цепях, а микроскопические токи − токи, обусловленные движением электронов в атомах и молекулах.
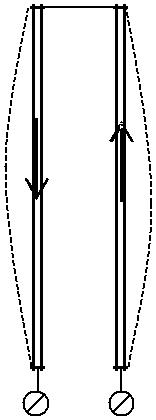
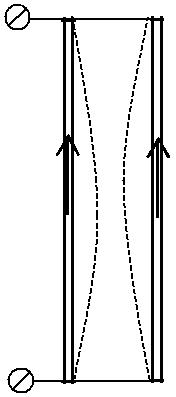
| I | I | I | I |
Рис. 1.1.5
Например, если вблизи какого -то тела поместить проводник с то-ком (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Магнитное поле макротока описыва-
ется вектором напряженности магнитного поля H. Для однородной изотропной среды вектор магнитной индукции связан с вектором на-
| пряженности магнитного поля соотношением | |
| B =μμ0H, | (1.1.1) |
где μ0 = 4π⋅10−7 Гн/м − магнитная постоянная, μ − магнитная прони-цаемость среды (безразмерная величина, показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды). Единица магнитной индукции в СИ [B] = 1 Тл, а единица на-пряженности магнитного поля [Н] = 1 А/м.
Для магнитного поля справедлив принцип суперпозиции маг-
нитных полей: магнитная индукция результирующего магнитного поля в некоторой точке, создаваемого несколькими токами или движущимися зарядами , равна векторной сумме магнитных индук-ций полей, создаваемых каждым током или движущимися зарядами в данной точке.
| n | ||
| B =∑Bi . | (1.1.2) |
i=1
Аналогично можно сформулировать принцип суперпозиции для напряженности магнитного поля.
1.2. Закон Био − Савара − Лапласа.
Согласно закону Био − Савара − Лапласа элемент проводника dl с током I создает в некоторой точке А индукцию поля, равную:
| I | |||||||||
| dB =μμ | dl | ×r | , | (1.2.1) | |||||
| 4πr3 | |||||||||
| где r − радиус-вектор, проведенный из элемента dl проводника в точ- | |||||||||
| ку А. Направление dB | перпендикулярно dl | и r | и совпадает с каса- | ||||||
| тельной к линии магнитной индукции (рис.1.2.1). | |||||||||
| dl | |||||||||
| r | |||||||||
| I | dB |
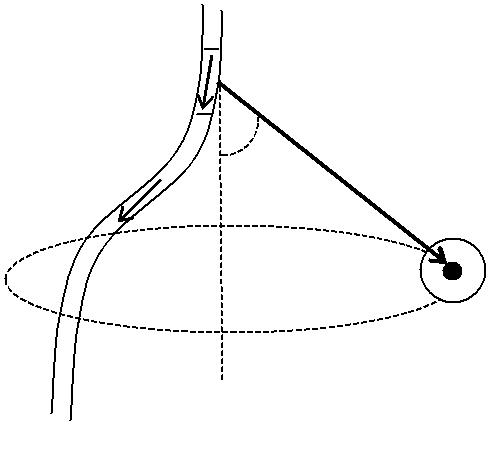
Рис. 1.2.1
| Модуль вектора dB определяется выражением | |||||||||||
| dB =μμ | I | dl sinα, | (1.2.2) | ||||||||
| 0 4πr2 | |||||||||||
| где α − угол между векторами dl | и r. | ||||||||||
| Для напряженности магнитного поля закона Био − Савара − Лап- | |||||||||||
| ласа будет иметь вид: | |||||||||||
| I | I | ||||||||||
| dH | = | dl ×r | и dH = | dl sinα. | (1.2.3) | ||||||
| 4 πr3 | 4πr2 | ||||||||||
Закон Био − Савара − Лапласа совместно с принципом суперпози-ции магнитных полей позволяет найти индукцию магнитного поля, создаваемого проводником любой конфигурации. В этом случае прин-
| цип суперпозиции магнитных полей будет иметь вид | |
| B =∫dB или H =∫dH. | (1.2.4) |
Дата добавления: 2017-01-08; просмотров: 2440;











