Магнитный поток. Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах.
Потоком вектора магнитной индукции (магнитным потоком) че-рез площадку dS называется величина, равная:
| d Φm = BdS = Bn dS, | (1.7.1) |
где Bn = Bcosα – проекция вектора B на направление нормали n к площадке dS, α − угол между векторами n и B (рис. 1.7.1). Магнит-ный поток равен числу линий магнитной индукции, пронизывающих замкнутую поверхность в направлении внешней нормали.
Bn
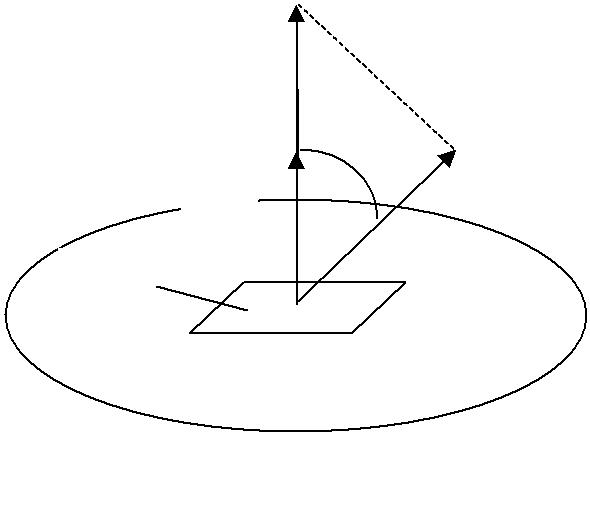
α B
n
dS
S
Рис. 1.7.1
Поток вектора магнитной индукции через произвольную поверх-ность S равен
| Φ m = ∫ BdS = ∫Bn dS . | (1.7.2) | |
| S | S | |
Если магнитное поле однородно (B = const), а поверхность S пло-ская, то магнитный поток равен
| Фm = BS cosα. | (1.7.3) |
За единицу магнитного потока принимается магнитный поток сквозь плоскую поверхность единичной площади, расположенную пер-пендикулярно к однородному магнитному полю, индукция которого равна единице. В системе СИ единица магнитного потока называется
вебером [Вб].
Магнитный поток через поверхность, ограниченную замкнутым контуром,называетсяпотокосцеплениемψэтого контура(потоком,сцепленным с контуром). Если контур имеет N витков, то потокосцеп-ление этого контура:
| Ψ = N Φm, | (1.7.4) |
где Фт − поток, пронизывающий один виток контура.
В природе отсутствуют элементарные «магнитные заряды», ана-логичные электрическим зарядам, поэтому линии индукции В магнит-ного поля не имеют ни начала, ни конца, т. е. магнитные силовые ли-нии замкнуты. Следовательно, поток Фт через любую замкнутую поверхность будет всегда равен нулю, так как число входящих линий
| равно числу выходящих силовых линий: | |||
| ∫ | |||
| BdS =0или∫ BndS =0. | (1.7.5) | ||
| S | S |
Теорема Гаусса для магнитного поля в интегральной форме:
поток вектора магнитной индукции сквозь любую замкнутую поверх-ность равен нулю.
| Так как B = μμ0H, | то поток вектора H через любую замкнутую | |
| поверхность также равен нулю: | ||
| ∫ HdS = 0 или ∫ HndS = 0. | (1.7.6) | |
| S | S |
Для записи теоремы Гаусса для магнитного поля в дифференци-альной форме воспользуемся теоремой Остроградского − Гаусса
∫ AndS = ∫divAdV .
S V
| ∫ | (1.7.7) | ||||
| BdS | = 0 ⇒ ∫ divBdV = 0 | ⇒ divB = 0. |
S V
Для напряженности магнитного поля получится аналогичное вы-ражение:
| divH =0. | (1.7.8) |
Выражения (1.7.7) и (1.7.8) являются дифференциальной формой теоремы Гаусса.
Дата добавления: 2017-01-08; просмотров: 3486;











