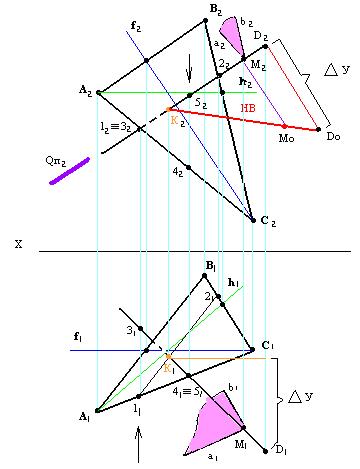
Расстояние от точки до плоскости.

Построить плоскость, параллельную ∆АВС и отстоящую от неё на n мм

Кратчайшее расстояние - перпендикуляр. Значит, из Д восстановим перпендикуляр к ∆АВС. - h2 (h1) , f1 f2) - перпендикуляр из Д1 к h1 Д2 к f2 - Qп2 1222 (1121) - на пересечении 1121 с Д1 К1 ( К2) - видимость перпендикуляра по узлам 12≡32 и 41≡51 - НВ ДК на П2 - на Д0К2 от К2 расстояние n Мо - из Мо // ДоД2 М2 (М1 по ли ниям связи на Д1К1) - из М1 пересекающиеся прямые (а1//А1С1, b1 //В1С1) - из М2 пересекающиеся прямые (а2//А2С2, b2 //В2С2)

Вопросы для самопроверки

1. Какие есть способы задания плоскости?

2. Что называется следами плоскости?

3. Какие плоскости называются плоскостью уровня?

4. Какие плоскости называются проецирующей плоскостью?

5. Определение горизонтали

6. Определение фронтали

7. Когда точка принадлежит плоскости?

8. Когда прямая принадлежит плоскости?

9. Когда прямая параллельна плоскости?

10. Когда прямая перпендикулярна плоскости?

11. Когда две плоскости параллельны между собой?

12. Когда две плоскости перпендикулярны между собой?

13. Как определить точку встречи прямой и плоскости?