Прямые особого положения

Горизонталь (h)– прямая, лежащая в данной плоскости и и параллельная горизонтальной плоскости проекции.

Фронталь(f) - прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.

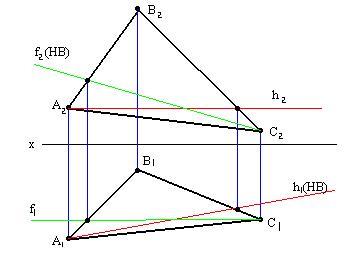
h₂ // X h₁ – НВ

f₁ // X f₂ - НВ

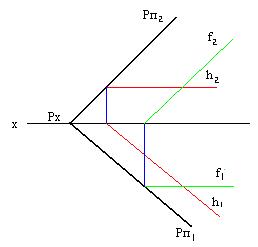
Все горизонтальные проекции горизонтали параллельны горизонтальному следу плоскости.

Все фронтальные проекции фронтали параллельны фронтальному следу плоскости.

Прямая и точка в плоскости

1. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости (или через одну точку этой плоскости параллельно прямой, лежащей в данной плоскости).

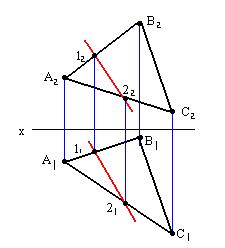
2. Точка принадлежит плоскости, если она принадлежит любой прямой этой плоскости.

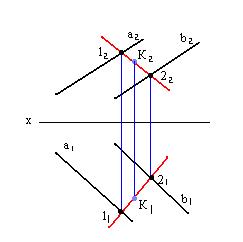
Взаимное положение прямой и плоскости,

Двух плоскостей

1. Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в данной плоскости.

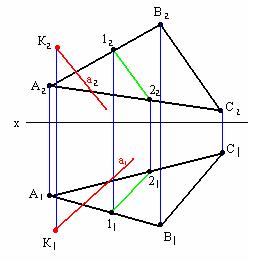
Дано: α (∆ АВС)

К (К₁ ; К₂)

а // α (через К провести

прямую параллельно α )

Алгоритм решения:

1 2 α а // α

2. Прямая, перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым данной плоскости.

В качестве таких прямых принимаем фронталь и горизонталь ( исходя из правила проецирования прямого угла).

Перпендикуляр к плоскости перпендикулярен любой прямой, проведенной в этой плоскости.

М₁ h₁

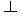M₂ f₂

3. Плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

α (∆ АВС) а // АВ (а₁ // А₁ В₁ , а₂ // А₂ В₂)

К (К₁; К₂ ) в // АС (в₁ // А₁ С₁ , в₂ // А₂ С₂)

α // ß

3. Плоскости перпендикулярны, если прямая, принадлежащая одной плоскости, перпендикулярна другой плоскости.

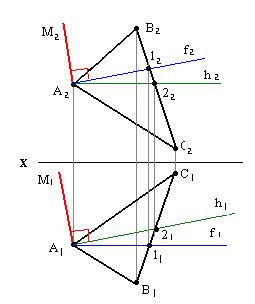
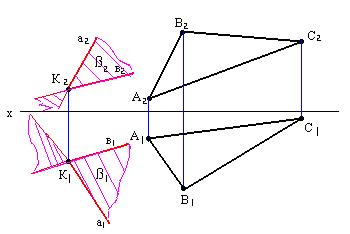
Задача: через прямую а провести плоскость, перпендикулярную ∆ АВС.

Искомую плоскость ß задаем двумя пересекающимися прямыми а и , опущенным к ∆ АВС.

Строим горизонталь h (h₁ и h₂ ) и фронталь f (f₁ и f₂)/

Исходя из правила построения перпендикуляра к плоскости, проводим прямую D₁ 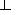h₁ и D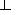₂ h₂.

Получаем искомую плоскость ß.