Плоскопараллельное перемещение

Плоскопараллельным называется такое движение фигуры в пространстве, при котором все её точки перемещаются в плоскостях, // между собой и // одной из плоскостей проекций.

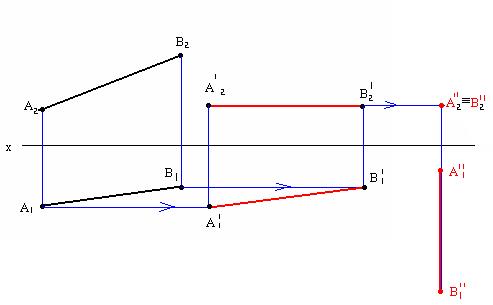
АВ перемещаем // П₂ до положения, при котором отрезок станет // П₁ –А₁¹ В₁¹.

Для этого фронтальную проекцию А₂ В₂ не изменяя её величины располагают на свободном поле чертежа на П₂ // оси Х. Из горизонтальной проекции А₁ В проведем прямые,// оси Х до пересечения с вертикальными линиями связи из А₂^/ В₂^/.

А₁^/ В₁^/ - НВ отрезка АВ.

Чтобы теперь сделать этот отрезок проецирующим, расположим А₁^/ В₁^/ перпендикулярно П₂. Из А₂^/ В₂^/ проведем прямые, параллельные оси Х до пересечения с линиями связи из А₁^// В₁^//.

АВ спроецировалась в точку А₂^{// ≡} В₂^//.

(Проекция фигуры на плоскости, относительно которой она перемещается, остается неизменной по своей величине и форме. А другие проекции точек этой фигуры перемещаются по прямым, параллельным оси Х ).

Найти НВ ∆ АВС и определить расстояние от точки S до ∆ АВС

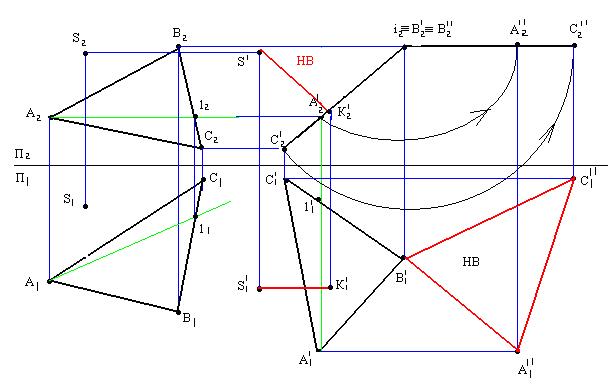
1.Разворачиваем ∆ АВС в положение перпендикулярное П₂ . Берм для этого горизонталь А1 и поворачиваем её перпендикулярно П₂ на свободном поле чертежа на П₁. Тогда ∆ АВС, содержащий эту горизонталь, будет перпендикулярен П₂.

(Проекцию А₁1₁ поворачиваем перпендикулярно оси Х и строим ∆ А^/₁В₁^/С₁^/ методом засечек. Этим же методом строим S₁^/).

Проекции А₂ , В₂ , С₂ перемещаются по прямым // оси Х. На пересечении этих прямых с линиями связи из А₁^/ , В₁^/, С₁^/, S₁^/ получаем точки А₂^/ , В₂^/, С₂^/, S₂^/.

∆АВС спроецировался в прямую А₂^/ В₂^/ С₂^/.

2.Поворачиваем ∆ АВС //П₁ (ось вращения проходит через В₂^/ перпендикулярно П₂). Фронтальная проекция А₂^/ В₂^/ С₂^/ не изменяет вид и величину при повороте, т.е. поворачиваем А₂^/ В₂^/С₂^/ // ОХ. При этом точки А^/₁ ,С₁^/ перемещаются по прямым, // ОХ.

На пересечении этих прямых с линиями связи из А₂^//, С₂^// получаем точки А₁^// и В₁^//.

∆ А₁^// В₁^/ С₁^// - НВ ∆ АВС.