Последовательность импульсов произвольной формы.
При любом изменении формы импульсов должны измениться модель сигнала 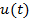 и результаты интегрирования по формулам Фурье. Это приведет к изменению АЧС и ФЧС. Неизменными останутся следующие свойства спектров:
и результаты интегрирования по формулам Фурье. Это приведет к изменению АЧС и ФЧС. Неизменными останутся следующие свойства спектров:
1) АЧС любой периодической последовательности имеет линейчатую (дискретную) и лепестковую структуру;
2) чем короче импульсы, тем шире спектр 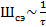 ;
;
3) чем "реже" следуют импульсы (больше 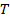 и меньше
и меньше  ,тем "гуще" спектр – ближе друг к другу спектральные линии;
,тем "гуще" спектр – ближе друг к другу спектральные линии;
4) изменение формы импульса  вызывает деформацию огибающей АЧС
вызывает деформацию огибающей АЧС  . 1
. 1
Одиночный импульс.
Для перехода от периодической последовательности к одиночному импульсу (рис. 3.16, б) надо неограниченно увеличивать период (  ). При этом происходят следующие изменения в спектре: . |
). При этом происходят следующие изменения в спектре: . |
1. Интервал между спектральными линиями, равный  ,сокращается, и в пределе они сливаются. Линейчатый спектр превращается в сплошной, для которого понятие "гармоника" теряет смысл, так как частоты
,сокращается, и в пределе они сливаются. Линейчатый спектр превращается в сплошной, для которого понятие "гармоника" теряет смысл, так как частоты 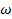 , на которых обнаруживается напряжение, принимают любые значения. Поэтому в уравнении АЧС − надо заменить
, на которых обнаруживается напряжение, принимают любые значения. Поэтому в уравнении АЧС − надо заменить  на
на 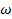 (или
(или  на
на 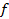 ). Частота
). Частота 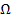 как интервал между гармониками становится бесконечно малой. Обозначим ее
как интервал между гармониками становится бесконечно малой. Обозначим ее 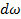 .
.
2. Значения составляющих по мере увеличения Т уменьшаются, становясь в сплошном спектре бесконечно малыми. Действительно,

3. Форма огибающей спектра не изменяется, так как частоты нулевых точек, равные  при неизменной длительности импульса
при неизменной длительности импульса 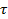 , не смещаются.
, не смещаются.
4. Ряд Фурье превращается в интеграл Фурье, так как слагаемые становятся бесконечно малыми, а функция − непрерывной. Этот переход приводит к следующему результату. Из формулы ряда Фурье для периодического сигнала

переходя к одиночному импульсу, получаем формулу
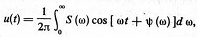
где  − спектральная плотность (или спектральная характеристика) импульса
− спектральная плотность (или спектральная характеристика) импульса 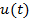 . Ее значение на произвольной частоте
. Ее значение на произвольной частоте 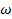 (или
(или 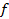 ) равно амплитуде колебания, приходящейся на 1 рад/с (или 1 Гц) в бесконечно узкой части спектра, содержащей частоту
) равно амплитуде колебания, приходящейся на 1 рад/с (или 1 Гц) в бесконечно узкой части спектра, содержащей частоту 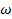 .
.
В ходе преобразования выражений следует учесть, что для одиночного импульса 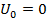 и
и  . Кроме того, надо разделить на
. Кроме того, надо разделить на 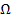 , считая
, считая  коэффициентом, и умножить подынтегральное выражение на
коэффициентом, и умножить подынтегральное выражение на 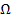 , заменив его на
, заменив его на 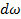 . Внеся период
. Внеся период  под знак интеграла и обозначив
под знак интеграла и обозначив 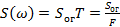 , убедимся в том, что огибающие спектров совпадают по форме и отличаются лишь масштабом, а также в том, что размерность
, убедимся в том, что огибающие спектров совпадают по форме и отличаются лишь масштабом, а также в том, что размерность  в В/Гц.
в В/Гц.
Обратное преобразование Фурье. Гармонический анализ − нахождение по заданной модели сигнала  частотного спектра
частотного спектра 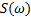 − называется прямым преобразованием Фурье. Для решения обратной задачи − синтеза сигнала
− называется прямым преобразованием Фурье. Для решения обратной задачи − синтеза сигнала  соответствующего заданному спектру
соответствующего заданному спектру 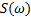 , требуется обратное преобразование. Его можно произвести способом замены переменной. Действительно, если в уравнении
, требуется обратное преобразование. Его можно произвести способом замены переменной. Действительно, если в уравнении  переменную
переменную  заменить на
заменить на  , а в уравнении
, а в уравнении 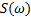 заменить
заменить  на
на  , то графики не изменятся, но спектр и модель сигнала "поменяются местами". В качестве примера на рис. 3.16, в показан результат обратного преобразования. Найден сигнал
, то графики не изменятся, но спектр и модель сигнала "поменяются местами". В качестве примера на рис. 3.16, в показан результат обратного преобразования. Найден сигнал  , спектр которого является равномерным от нуля до частоты
, спектр которого является равномерным от нуля до частоты 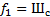 . Поскольку огибающая спектра имеет форму прямоугольника, модель сигнала
. Поскольку огибающая спектра имеет форму прямоугольника, модель сигнала  . Такой подход позволяет определять сигналы, обладающие оптимальным для заданных условий частотным спектром.
. Такой подход позволяет определять сигналы, обладающие оптимальным для заданных условий частотным спектром.
Дата добавления: 2021-04-21; просмотров: 494;











