Аналоговые сигналы.

Аналоговые сигналы (АС) изменяются во времени аналогично передаваемому сообщению. К числу непрерывных АС относятся телефонные, звукового вещания, видеосигналы. Все эти сигналы являются случайными процессами, а их характеристики, полученные на основе статистической обработки результатов множества измерений, − вероятностными.

Телефонные сигналы, называемые также абонентскими или речевыми, существенно различаются в зависимости от высоты, тембра и других характеристик голоса и могут содержать частоты 80... 12 000 Гц. Однако если пропустить в канал связи при помощи канального фильтра речевой спектр 300...3400 Гц, то разборчивость по фразам составит 99%. Зато сужение полосы пропускания снизит уровень помех и позволит увеличить число каналов в рабочем диапазоне частот. Динамический диапазон речевого сигнала 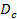= 26...35 дБ.

Сигналы звукового вещания отличаются от телефонных более широким спектром − от 15...20 Гц до 15...20 кГц и 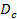= 86...96 дБ. В соответствии с действующими нормами в процессе формирования сигналов звукового вещания производится их вынужденное сужение соответственно до 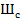= 30... 15 000 Гц и 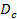= 50...60 дБ. При этом сохраняется вполне удовлетворительное качество звучания. Передача полного спектра и динамического диапазона становится возможной при использовании цифровых сигналов.

Телевизионные видеосигналы образуются путем последовательного разложения оптического черно-белого изображения по строкам и кадрам. Разложение по строкам с изменением яркости вдоль них позволяет передавать неподвижное изображение. Для передачи подвижного изображения используют смену кадров с последовательно смещаемыми изображениями. Стандартом СССР предусмотрено разложение изображения в кадре на 625 строк при частоте кадров 25 Гц. Нижние частоты спектра (доли герц) соответствуют передаче однотонного фона во весь экран длительностью в несколько секунд.

Верхняя частота − сигналу типа шахматной доски с размером элемента, равным ширине строки. Один период соответствует паре элементов − черному и белому. С учетом формата (отношения сторон) кадра 4/3 частота 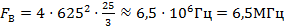. У передаваемого сигнала .

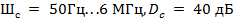Сигналы цветности передаются в пределах того же спектра, но имеют иную модуляцию, что позволяет их отделить в приемнике. В конце каждой строки одновременно передаются импульсы гашения луча и строчной синхронизации. Последний управляет перемещением луча в начало следующей строки. Аналогично управление кадровой разверткой.

Достоинства АС в их простоте. Аналоговая техника несложна и экономична. За длительный период развития она отработана настолько, что возможности ее совершенствования практически исчерпаны.

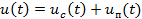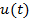Основной недостаток АС − низкая помехоустойчивость связи, обусловленная изменением амплитуды АС в пределах широкого динамического диапазона. Остановимся на этом подробнее. Для подавления помехи необходимо ее "опознать", т. е. отличить от сигнала по какому-либо признаку. Если на входе канала действует сумма сигнала и помехи: , то изменяется одинаково как за счет изменения 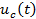так и за счет 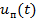и "опознать", а тем более подавить помеху невозможно. Она "равноправна" с сигналом. Один из путей решения этой проблемы − поиск таких сигналов 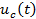, изменение которых в процессе передачи происходило бы при постоянной амплитуде за счет изменения другого параметра. Если бы это удалось, то действие помехи, влияющей на амплитуду, можно было бы подавить при помощи амплитудного ограничителя, не искажая сигнал. Такие возможности открывает применение дискретных сигналов.

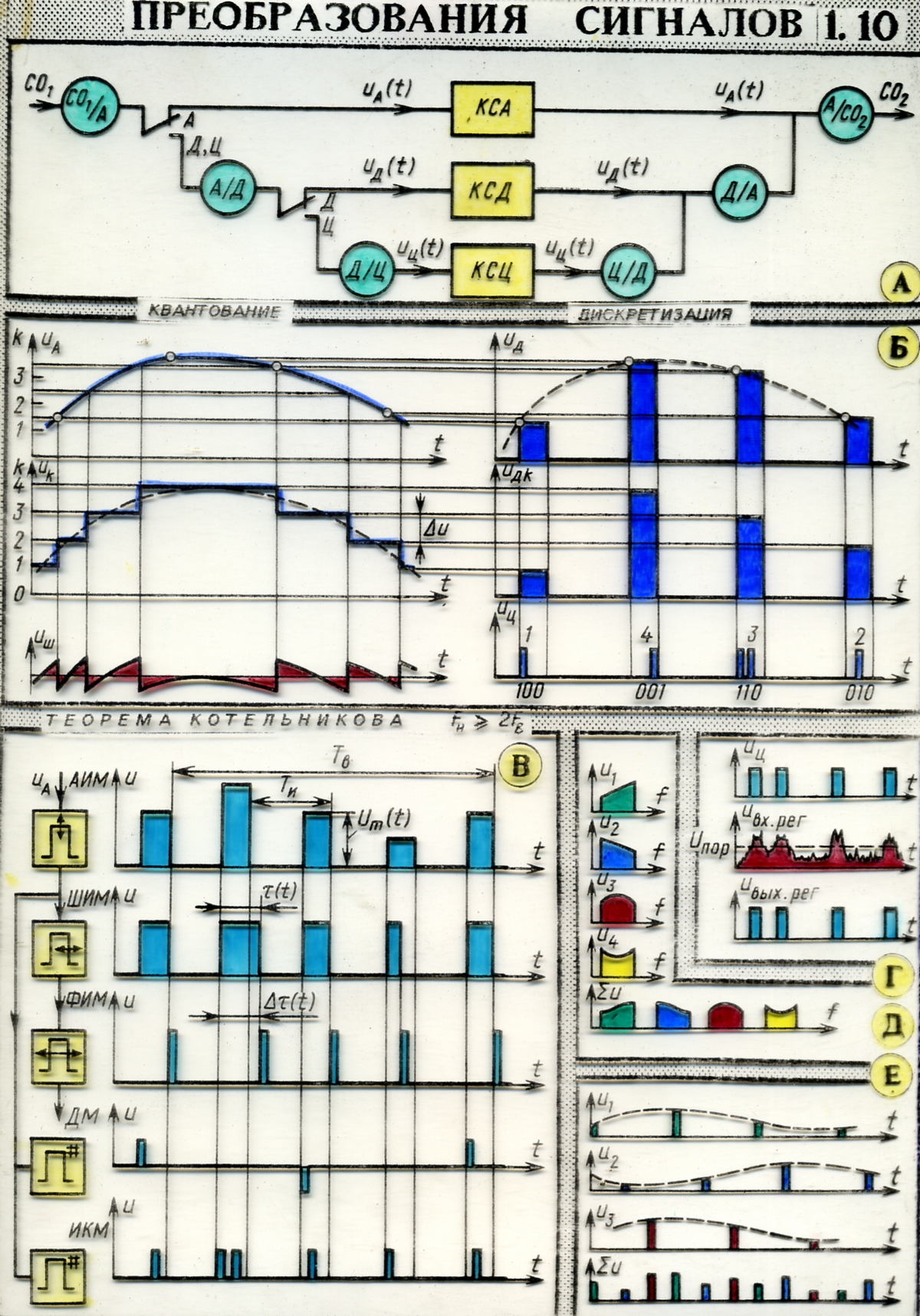
Дискретные и цифровые сигналы. Преобразование АС в дискретные (ДС) и цифровые (ЦС) иллюстрируется структурной схемой рис. 3.17, а. Первое превращение входного сообщения СО₁/А в АС производит, например, микрофон. Аналоговый сигнал может быть передан по аналоговому каналу связи (КСА) или поступить через переключатель в дискретный канал (КСД), на входе которого использован преобразователь А/Д, например импульсный модулятор. Дискретный сигнал преобразуется в цифровой при помощи аналого-цифрового преобразователя Д/Ц (или кодера).

Дискретизация непрерывного АС состоит в преобразовании его (рис. 3.17, б) в импульсы, следующие друг за другом через период дискретизации и промодулированные значениями сигнала в моменты дискретизации по одному из параметров (на рис 3.17, б − по амплитуде).

Как следует выбрать период дискретизации 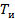для того, чтобы после обратного преобразования ДС в АС не возникло искажений? Ответ на этот вопрос содержится в теореме Котельникова, которая гласит: произвольный сигнал, спектр которого не содержит частот выше 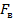может быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени 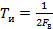(рис. 3.17, в)

Действительно, если 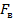− высшая частота спектра, то ей соответствуют самые быстрые изменения сигнала. Поэтому при выборе 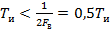будет передано не менее двух импульсов за период сигнала и все его изменения могут быть восстановлены.

Если спектр сигнала не ограничен, то выбирают эффективную ширину спектра 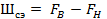так, чтобы искажения, возникшие на частотах 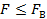не превышали допустимой нормы. Этому условию для телефонного сигнала соответствует 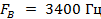. Поэтому для него 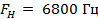, а .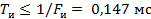

Квантование (или дискретизация по уровню) аналогового сигнала состоит в том, что плавно изменяющийся АС преобразуется в сигнал, изменяющийся скачкообразными приращениями − квантами 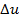(рис. 3.17, б). Любое значение квантованного сигнала 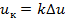, где к − целое число уровней. Чем меньше 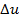и больше 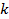, тем точнее АС воспроизводится квантованным сигналом. I

При квантовании произвольное значение АС 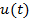округляется до ближайшего разрешенного уровня 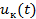. Остаток 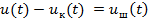называется шумом квантования (рис. 3.17, б). Его значение 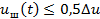, поэтому чем меньше 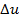и больше 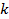, тем слабее шум квантования.

Динамическому диапазону квантованного сигнала при известном 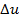соответствует последовательность целых чисел 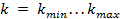которые чередуются, повторяя изменение 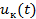. При передаче этой последовательности чисел вместо сигнала 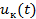получим цифровой сигнал (ЦС). Например, в случае, показанном на рис. 3.17, б, уровни: 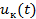в моменты дискретизации чередуются в последовательности: 1, 2, 3, 4, 3, 2, 1. При помощи аналого-цифрового преобразователя (кодера) (АЦП) их можно превратить в ЦС 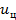, в котором каждая цифра, записанная в двоичном коде, отображается определенным сочетанием единиц (импульсов) и нулей (пауз).

Такие сигналы имеют ряд существенных достоинств. Во-первых, они имеют постоянную амплитуду, что позволяет повысить помехоустойчивость, применив амплитудное ограничение или значительно более эффективную меру − регенерацию импульсов. Регенерация − это формирование неискаженных импульсов на выходе канала или в промежуточных ретрансляторах, управляемых сигналом, искаженным помехами. Решение о формировании очередного импульса принимается в момент приема импульса в том случае, когда сумма 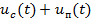превышает пороговое значение. Как видно из рис. 3.17, г, за счет регенерации можно восстановить сигнал на фоне весьма интенсивных помех. Во-вторых, после передачи по каналу связи ЦС может быть непосредственно обработан ЦВМ, записан в ее память и преобразован в исходной АС при помощи цифро-аналогового преобразователя (ЦАП) непосредственно или в любое время по требованию потребителя. Связанные с этим возможности повышения помехоустойчивости, качества и пропускной способности каналов связи значительны. Недостаток ЦС − широкий частотный спектр. Если верхняя частота AC 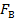, число разрешенных уровней квантования (пачек импульсов за период) 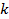, а число двоичных разрядов (импульсов в пачке) 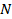, то частота следования импульсов ДС равна 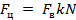. Для цифровых магнитофонов и лазерных проигрывателей 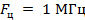. Такова же скорость передачи информации − 1 Мбит/с.

Современные системы кабельной, радиорелейной и космической связи являются многоканальными. По ним одновременно передается множество сигналов. Один из способов такой передачи − временное уплотнение каналов. Для этого в каждом канале используют детерминированные сигналы, причем во время пауз между импульсами данного сигнала передают импульсы других каналов. При заданном периоде 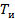число каналов тем больше, чем меньше длительность импульсов 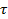и межимпульсных интервалов.

В современных многоканальных системах широко используются ЦС. В отличие от одноканальной системы: в которой каждое число формируется в течение времени существования данного уровня 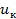(рис. 3.17,6), в многоканальной на это отводится гораздо меньшее время 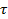. Основой для формирования многоканальных ЦС является показанный на рис. 3.17,6 сигнал, детерминированный по времени и квантованный по уровню – .

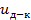Уровни квантованных импульсов 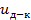чередуются в последовательности 1-4-3-2, который соответствует цифровой сигнал 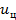. Потеря части уровней 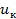несущественна, так как условие 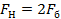выполняется.

Способы модуляции импульсных сигналов. Предшественниками ЦС являются используемые в кабельных и радиорелейных системах связи ДС в виде последовательности модулированных импульсов. На рис. 3.17,в показаны переменные диаграммы исходного сигнала с модуляцией: амплитудной (АИМ); широтной или длительностной (ШИМ или ДИМ); фазовый или временной (ФИМ или ВИМ); дельта-модуляцией (ДМ) и импульсно-кодовой (КИМ).

Во всех случаях, кроме АИМ, амплитуды импульсов постоянны−в этом их достоинство. Мгновенному значению исходного сигнала пропорциональны соответственно при АИМ− амплитуда, при ДИМ−длительность и при ФИМ−фазовый (временной) сдвиг.

При ДМ периодическая последовательность положительных импульсов существует до тех пор, пока растут значения сигнала − есть приращение "дельта". Этот способ модуляции позволяет обеспечить более высокую по сравнению с предыдущими помехоустойчивость.

При ИКМ производится кодирование каждого квантованного уровня сигнала определенным сочетанием импульсов, которое определяется используемым кодом. Чаще всего применяют двоичный цифровой код и получают ЦС − частный случай ИКМ-сигнала.

Способы формирования многоканальных сигналов. Существует два способа формирования многоканальных сигналов − с частотным и вре менным разделением каналов. В результате разделения канал связи формируется многоканальный управляющий сигнал, предназначенный для передачи по кабельным линиям и модуляции радиочастных колебаний в РПДУ радиорелейных и космических систем связи.

Частотное разделение каналов заключается в смещении спектров сигналов по оси частот и сложении в многоканальный групповой сигнал. Смещение спектров обеспечивает возможность их разделения фильтрами в приемнике (рис. 3.17, д). Например, спектры телефона сигналов смещают в соседних каналах на 4 кГц, обеспечивая интервал между каналами шириной в 4000 − (3400−300) = 900 Гц, необходмый для расфильтровки.

Из 12-канальных первичных групп аналогичным образом формируют вторичные и т. д. группы, состоящие из множества каналов, число которых кратно 12. Например, в одной из радиорелейных линий формируется 1920 телефонных каналов. Наряду с телефонными могут передаваться телеграфные, фототелеграфные, вещательные сигналы Для телевизионных сигналов отводятся широкополосные «стволы».

Временное разделение каналов (рис. 3.17, е) производится, как уже отмечалось, путем заполнения межимпульсных интервалов данного дискретного сигнала импульсами других сигналов. Как показывает анализ, для увеличения числа каналов требуется сокращение длительности импульсов 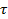, что приводит к чрезмерному расширению спектра. Поэтому такие системы малоканальны.

Передача цифровых сигналов отличается квантованием исходных дискретных сигналов в каждом канале с последующим кодированием. За время 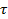передаются серия импульсов соответствующая двоичному числу, отображающему мгновенное квантованное значение сигнала в данном канале 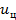(рис. 3.17, б). Первичная группа содержит 32 телефонных канала, вторичная − 120 и т. д.

По сравнению с частотным разделением временное разделение цифровых сигналов обеспечивает большую помехоустойчивость, высокое и гарантированное качество сигнала; такие линии просто сопрягаются с ЦВМ, в них используется надежная малогабаритная и недорогая элементная база микроэлектроники. К недостаткам многоканальных систем с временным разделением цифровых каналов относится широкий частотный спектр, обусловленный необходимостью применения очень коротких (вплоть до наносекундных, 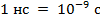) импульсов.

Выводы

Сигнал − это физический процесс, однозначно соответствующий передаваемому сообщению. Временная функция 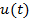является математической моделью сигнала. Сигнал детерминирован (определен), если модель задана, и случаен, если неизвестна.

Сигналы могут быть непрерывными или импульсными, аналоговыми, дискретными или цифровыми, периодическими или непериодическими.

Параметрами сигнала являются амплитуда, частота, начальная фаза и длительность. У гармонического колебания 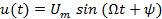длительность не ограничена, значения параметров постоянны. У сложных сигналов длительность ограничена, амплитуда изменяется в пределах динамического диапазона, а частота и фаза определяются в пределах частотного спектра.

Логарифмическая шкала децибел соответствует закономерности восприятия человеком изменения уровня сигнала:

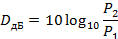
Сигнал не искажается в канале связи при выполнении условия согласования − объем сигнала должен "вписываться" в объем канала по всем параметрам:

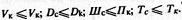
(для видео сигналов, кроме того, не должно быть фазовых искажений)

Любой периодический сигнал 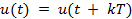можно синтезировать путем сложения постоянной составляющей и совокупности гармоник − членов ряда Фурье:

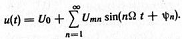
Временная и спектральные диаграммы сигнала дают полную информацию о его параметрах, а сравнение диаграмм сигналов на входе и выходе канала − о наличии и характере искажений.

Задача гармонического анализа периодического сигнала состоит в определение составляющих 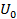и 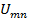ряда по известной модели сигнала 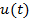(прямое преобразование Фурье) и решается с использованием формул Фурье. Результаты наглядно представляются в виде спектральных диаграмм.

Спектр колебания типа меандр содержит нечетные гармоники. Их амплитуд убывают пропорционально .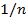

Спектр периодической последовательности импульсов является лепестковым, линейчатым и теоретически неограниченным. Форма его огибающей определяется длительностью и формой импульсов. Спектр тем "гуще", чем ниже частота 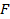. Эффективная ширина спектра (та его часть, в которой содержится заданная часть энергии) шире, чем короче импульс .

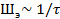Спектр одиночного импульса сплошной. Его огибающая такая же, как у спектра периодической последовательности импульсов той же формы. Сплошные слектры характерны также для непериодических сигналов и помех. Энергия спектра импульсных помех сосредоточена в основном в низкочастотной части радиодиапазона, а шумовых − распределена равномерно.

Обратное преобразование Фурье позволяет синтезировать сигнал, т. е. определить его модель 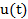по заданному спектру 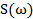. Для этого используют, в частности, способ замены переменных.

К аналоговым относятся телефонные, вещательные и видеосигналы. Они являются случайными процессами, и их параметры определяют статистическими методами.

Дискретные (прерывистые) во времени сигналы − это импульсы, повторяющиеся с периодом дискретизации 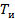и изменяющиеся в соответствии со значениями АС в моменты дискретизации. В соответствии с теоремой Котельникова восстановление ДС без искажений возможно, если .

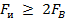Квантованные сигналы могут иметь только разрешенные квантовые уровни, число которых ограничено. Они имеют "ступенчатую" форму, являясь переходной разновидностью от аналогового к цифровому сигналу, могут быть непрерывными или дискретными

Цифровой сигнал − результат преобразования (кодирования) квантованного сигнала в группы импульсов, отображающие запись каждого уровня двоичным числом. Использование цифровых сигналов позволяет повысить помехоустойчивость н качество передачи, использовать ЦВМ для обработки и хранения сигналов.

В многоканальных системах связи сигналы формируют методами частотного или временного разделения каналов. При частотном разделении спектры аналоговых сигналов располагаются по оси частот с малыми интервалами. При временном разделения импульсы различных аналотвых сигналов передаются поочередно. Дискретные сигналы могут представлять собой модулированные импульсы (АИМ, ШИМ, ФИМ или ДМ) или цифровые сигналы.

Глава 4. РАДИОСИГНАЛЫ

4.1. АМПЛИТУДНО-МОДУЛИРОВАННЫЙ РАДИОСИГНАЛ

Общие сведения.

В соответствии с третьим принципом радиотехники радиосвязь возможна при использовании радиосигнала (PC) − колебания радиочастоты, один из параметров которого изменяется (модулируется) во времени управляющим сигналом, который соответствует передаваемому сообщению. В случае непрерывного PC модулируемых параметров три: амплитуда U_m, частота 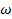(или 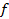) и начальная фаза 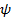. Соответственно различают сигналы с амплитудной (АМС), частотной (ЧМС) и фазовой (ФМС) модуляцией.

Исходное гармоническое радиочастотное колебание называется несущим, его параметры 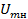, , 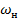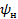. Процесс модуляции состоит в принудительном изменении управляемого параметра, в данном случае амплитуды 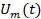и сопровождается (это будет доказано) расширением частотного спектра.

Однако ширина спектра PC, как правило, не превышает 10% частоты 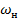, поэтому − узкополосные сигналы. Узкополосность − положительное свойство PC, поскольку позволяет использовать радиоканалы с узкой полосой пропускания и за счет этого ограничить уровень помех в пределах полосы и подавить их за ее пределами.

Тональный АМС

Математическая модель. Начнем с простейшего случая − тонального АМС. В этом случае оба колебания: несущее 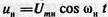и низкочастотное − модулирующее 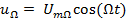, являются гармоническими. На рис. 4.1, а показаны временные диаграммы этих колебаний, а также АМС, огибающая которого без искажений повторяет изменения .

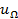Составим уравнение − математическую модель такого АМС: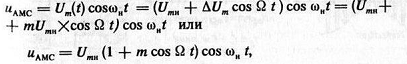

где 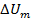− амплитуда огибающей − максимальное значение приращения амплитуды АМС в процессе модуляции; 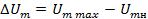; 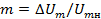− коэффициент модуляции − относительное значение амплитуды огибающей.

Поскольку − 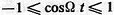, амплитуда АМС изменяется от 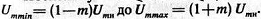Форма огибающей оказывается неискаженной, если 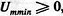, т. е. если 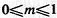(или от 0 до 100 %). Если это условие не выполняется ( 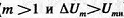), to возникают искажения огибающей, обусловленные так называемой перемодуляцией (рис. 4.1, в).

Пример. Требуется составить уравнение АМС, если известны его параметры:

.

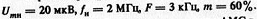Решение 1. Записываем уравнение АМС в общем виде: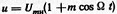

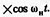
2. Записываем значения параметров в основных единицах: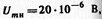

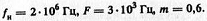
3. Подставляем их в уравнение и получаем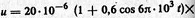

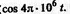
Частотный спектр. Как и любой сложный периодический сигнал, АМС можно подвергнуть гармоническому анализу для определения частотного спектра. Для этого в уравнении АМС раскроем скобки: .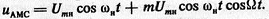

Здесь первое слагаемое соответствует несущему колебанию, а второе возникло в результате модуляции. Учитывая, что 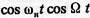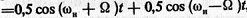, получаем уравнение спектра:

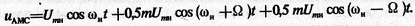
Итак, при тональной модуляции в спектре АМС (рис. 4.1, б) кроме неизменяемого в процессе модуляции несущего колебания существуют два боковых колебания: верхнее и нижнее с равными амплитудами 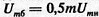и частотами, симметричными относительно несущей 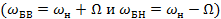. В процессе передачи любому изменению уровня (например, громкости) сигнала соответствует пропорциональное изменение т и 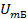, а изменению частоты 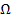− изменение частот 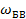и 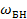. Поэтому именно боковые колебания являются

полезными составляющими спектра АМС.

Ширина спектра 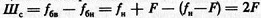вдвое больше, чем у модулирующего сигнала.

Параметры. Амплитудно-модулированный тональный сигнал (рис. 4.1, а) как любой детерминированный сигнал однозначно определяется совокупностью следующих параметров, входящих в уравнение:

1) амплитудой несущего колебания 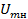, измеряемой вольтметром или оцениваемой по осциллограмме при отсутствии модуляции, когда ,

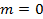2) частотой несущего колебания 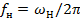, которую измеряют частотомером,

3) частотой модулирующего колебания 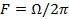, которая также может быть измерена частотомером,

4) коэффициентом модуляции 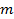, пропорциональным уровню управляющего сигнала. Для измерения 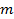используют измеритель модуляции или осциллограф. По осциллограмме (рис. 4.1, в) следует отсчитать наибольшее 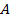и наименьшее 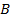значения размаха (удвоенной амплитуды) и рассчитать ,

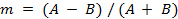5) дополнительными параметрам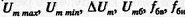и и 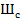которые можно рассчитать через основные.

Пример. По условиям предыдущего примера определить дополнительные параметры АМС.

Решение. 1. Максимальное и минимальное значения амплитуды

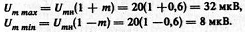
2. Амплитуда огибающей

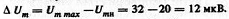
3. Амплитуды боковых колебаний

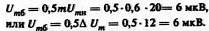
4. Частоты боковых колебаний

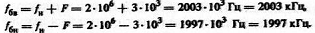
5. Ширина спектра

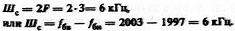
Векторное представлениеАМС. Представим каждое их трех гармонических колебаний, образующих спектр АМС, в виде векторов, длины которых пропорциональны амплитудам 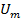, а скорости вращения − частотам 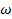. Если частоты колебаний не равны ( 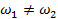), то взаимное расположение векторов изменяется за счет их относительного вращения с разностной скоростью 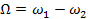случае тонального АМС таких скоростей две: 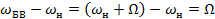и 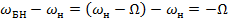. Это означает, что векторы боковых колебани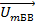й и 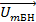вращаются по отношению к вектору 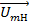во встречных направлениях с разными скоростями.

На 8 показан ряд последовательных положений вектора 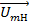через интервал 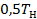, положения векторов 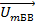, 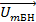и их суммы − приращения амплитуды 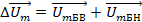, в те же моменты времени. Как видим, векторы 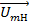и 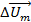всегда направлены по одной прямой, но вектор приращения изменяется по закону 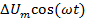. В результате их сложения формируется огибающая АМС: .

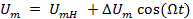Применения АМС. 1. В измерительных генераторах радиочастоты тональный АМС используется в качестве тест-сигнала для испытания РПУ. Генераторы формируют сигналы, у которых значения 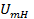и 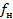можно регулировать в пределах широкого диапазона, 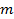от 0 до 100%. Встроенный модулятор обеспечивает "внутреннюю" модуляцию с частотами 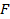, равными 400 или 1000 Гц. "Внешняя" модуляция возможна на любой звуковой частоте.

2. При тональном телеграфировании модуляции телеграфных сигналов обеспечивает их "озвучание", т. е. возможность их приема на слух обычным РПУ AM сигналов.