Последовательность униполярных прямоугольных импульсов.

Названная последовательность (рис. 3.16, а) находит широкое применение в дискретных и цифровых радиосистемах. Для анализа выберем начало отсчета так, чтобы функция была четной.

Ее уравнение

Поэтому пределы интегрирования 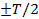надо ограничить длительностью импульса 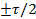. Постоянная составляющая

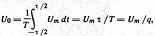
где − скважность − параметр импульсных сигналов, показывающий, во сколько раз импульсы короче периода их повторения. Для радиолокационных сигналов типичны значения: . Амплитуды гармоник

Подставив , получим уравнение частотного спектра:

где 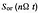− закон изменения огибающей АЧС (на рис. 3.16, а − штриховая линия).

Из анализа этого уравнения вытекают следующие свойства АЧС и ФЧС импульсов при высокой скважности (рис. 3.16, а):

1. При повышении частоты (увеличении п) амплитуды гармоник изменяются по затухающему колебательному закону, проходя через нулевые значения, когда 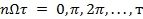.е. на частотах 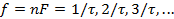Такая структура спектра называется лепестковой.

2. Амплитуды низших (1-, 2-, 3-й и т. д.) гармоник практически одинаковы и равны . Действительно, если при 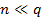, то .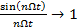

3. Теоретически ширина спектра не ограничена. Практически ее ограничивают участком, в пределах которого содержится заданная часть энергии колебания. Например, если принять, что эффективная ширина спектра (рис. 3.16, а то в ее пределах окажется около 90% энергии.

4. Фазы гармоник изменяются на 180°, когда изменяет знак, т. е. на частота 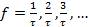Фазочастотный сигнал показан на рис. 3.16, а..