Рекомендации к выполнению анализа спектральной плотности
При выполнении пункта a) настоящего раздела 2 – при получении функции изображения по Лапласу S(p) –врамкахнастоящей работыучащиеся должны попрактиковаться в использовании свойств прямого преобразования Лапласа (таблица 2.1) и известных (табличных) изображений типовых оригиналов (таблица 2.2).
В вариантах заданий курсовой работы встречаются следующие разновидности импульсных сигналов (оригиналов):
- сигналы, содержащие интервалы с постоянными значениями и точки разрыва первого рода, но не содержащие интервалы с линейно-меняющимися функциями (рисунок Рисунок 2.1);
Таблица 2.1 – Свойства прямого преобразования Лапласа
| Название свойства | Аналитическое выражение | Примечание |
| 1. Линейности | 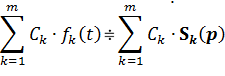
| 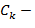 константа, константа,
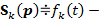 изображение оригинала изображение оригинала 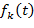 , ,
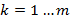 . .
|
| 2. Смещение функции времени (теорема запаздывания) | 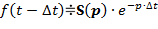
| 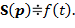
|
| 3. Дифференцирование функции времени (свойство производной) | 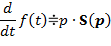
| 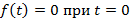 , ,
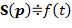 . .
|
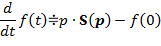
| 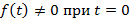 , ,
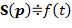 . .
| |
| 4. Интегрирование функции времени (свойство первообразной) | 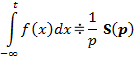
| 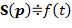 . .
|
Таблица 2.2 – Спектральные характеристики типовых измерительных сигналов
| Оригинал | Диаграмма функции оригинала | Функция оригинала | Изображение |
| Единичная ступенчатая функция (функция Хевисайда) | 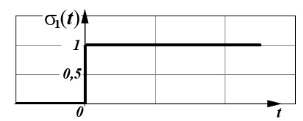
| 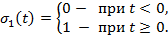
| 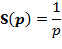
|
| Единичная импульсная функция (дельта-функция) | 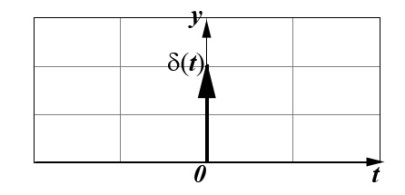
| 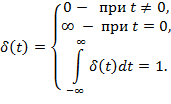
| 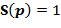
|
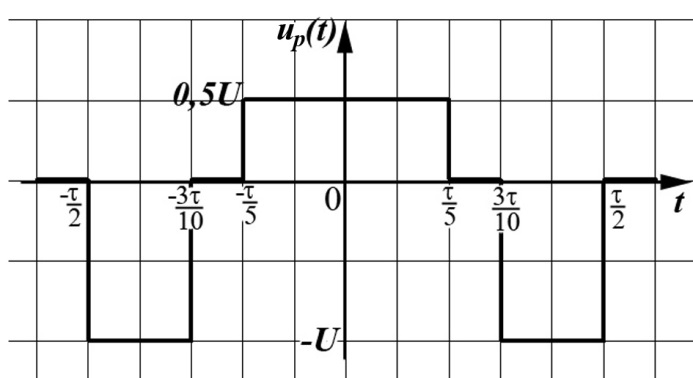
Рисунок 2.1 – Импульс, который возможно представить комбинацией ступенчатых функций
- сигналы, содержащие интервалы с линейно-меняющимися функциями (рисунок Рисунок 2.2). Интервалы с постоянными значениями и точками разрыва они могут либо содержать (рисунок Рисунок 2.2,а), либо не содержать (рисунок Рисунок 2.2,б).
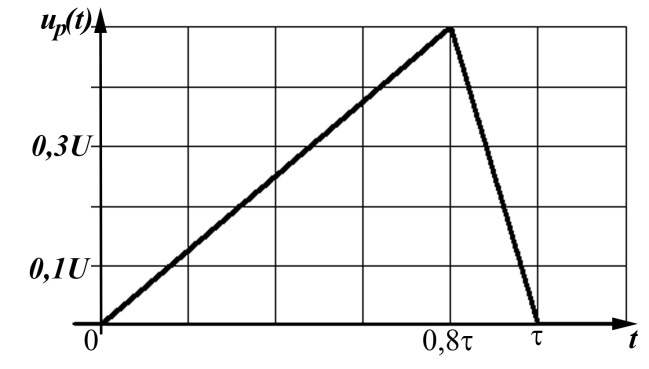 а)
а)
| 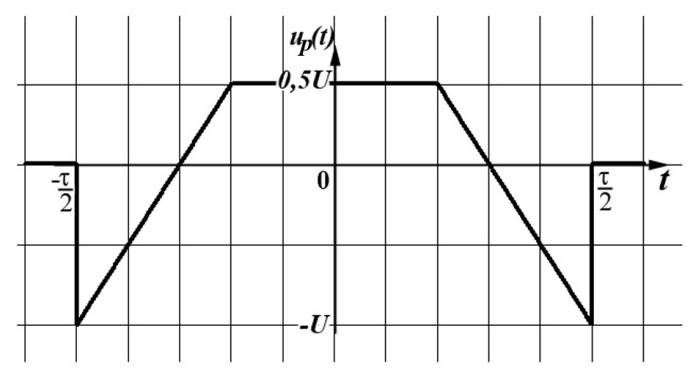 б)
б)
|
Рисунок 2.2 – Импульсы, содержащие наклонные отрезки
2.2.1 Функции изображений по Лапласу и по Фурье импульса, представляемого комбинацией ступенчатых функций (рисунок Рисунок 2.1)
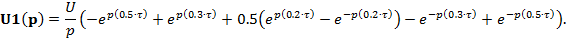
| (3.1) |
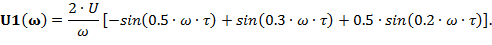
| (3.2) |
2.2.2 Функции изображений по Лапласу и по Фурье импульса, представляемого комбинацией наклонных отрезков, без точек разрыва (рисунок Рисунок 2.2,а)
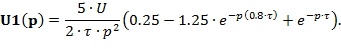
| (3.3) |
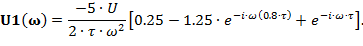
| (3.4) |
2.2.3 Функции изображений по Лапласу и по Фурье импульса, представляемого комбинацией наклонных отрезков, без точек разрыва (рисунок Рисунок 2.2,б)
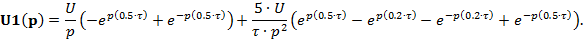
| (3.5) |
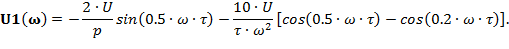
| (3.6) |
Дата добавления: 2016-12-27; просмотров: 1450;











