Получение функции ФЧХ
С точки зрения математика ФЧХ – это аргумент комплексной частотной характеристики H(w). Цель задания подраздела – учащиеся должны получить и развить навыки самостоятельного вычисления ФЧХ. Аргумент дроби (4.20) можем определить как разность аргументов числителя и знаменателя.
a) Числитель (4.20) чисто мнимый и положительный, поэтому аргумент числителя равен 0.5·π, или 90°. Начнём вводить выражение для ФЧХ (рисунок Рисунок 4.18,а).
b) В знаменателе дроби (4.20) присутствует и действительная, и мнимая части. Поэтому аргумент знаменателя определим классическим способом – как арктангенс от деления мнимой части на действительную. Дописываем выражение:
- в вводимом выражении ФЧХ на месте вычитаемого набираем строчку «atan» и набираем с клавиатуры скобки «(» и «)» (рисунок Рисунок 4.18,б);
- вставляем с панели «Calculator» операцию деления «/» (рисунок Рисунок 4.18,в);
- вводим в числитель мнимую часть знаменателя выражения (4.20) – сумму всех множителей перед мнимой единицей «i», с учётом знаков (рисунок Рисунок 4.18,г). При этом во всех множителях мнимая единица «i» должна быть исключена! Выражение мнимой части имеет вид выражения (4.23);
- вводим в знаменатель сумму всех слагаемых действительной части знаменателя, с учётом знака (рисунок Рисунок 4.18,д);
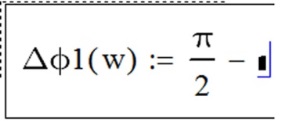 а)
а)
|  б)
б)
| 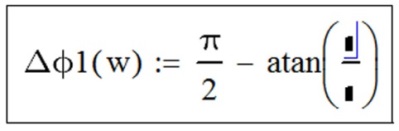 в)
в)
|
 г)
г)
| ||
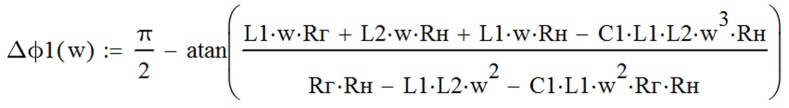 д)
д)
|
Рисунок 4.18
- знаменатель примет вид выражения (4.22), а введённая версия функции ФЧХ – следующий вид
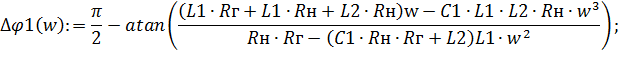
| (4.27) |
c) Но введенная функция не для всех частот будет адекватно воспроизводить ФЧХ из за наличия в ней функции арктангенса. Функция
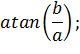
| (4.28) |
адекватно воспроизводит аргумент комплексного выражения
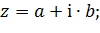
| (4.29) |
только при a>0. В обратном случае, при
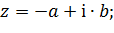
| (4.30) |
вектор 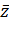 будет находиться во второй, либо в третьей четверти (рисунок 4.16). Функция (4.28) имеет область значений
будет находиться во второй, либо в третьей четверти (рисунок 4.16). Функция (4.28) имеет область значений
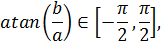
| (4.31) |
то есть для векторов, находящихся только в первой, либо в четвёртой четвертях.
Поэтому для функции арктангенса (4.28) будет справедливо следующее
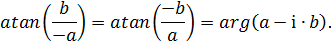
| (4.32) |
То есть значение (4.32) будет соответствовать аргументу (углу) анти вектора 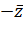 (рисунок Рисунок 4.19), и будет отличаться от действительного значения на 180°. Таким образом, для случаев, когда знаменатель в функции арктангенса (4.27) отрицательный, к функции
(рисунок Рисунок 4.19), и будет отличаться от действительного значения на 180°. Таким образом, для случаев, когда знаменатель в функции арктангенса (4.27) отрицательный, к функции 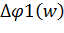 необходимо прибавлять π, либо –π (без разницы). Функцию ФЧХ при этом можем описать так
необходимо прибавлять π, либо –π (без разницы). Функцию ФЧХ при этом можем описать так
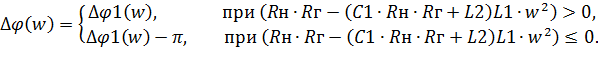
| (4.33) |
Выражение в неравенствах – действительная часть знаменателя КЧХ (4.20).
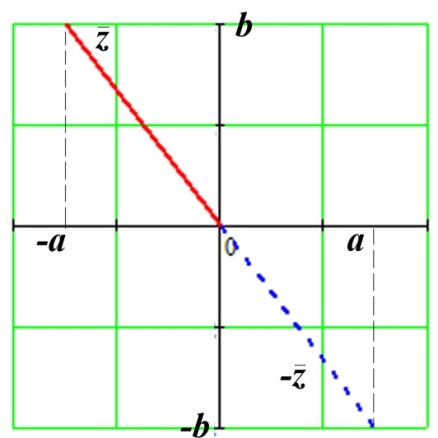
Рисунок 4.19
d) Функцию (4.33) в программе MathCad опишем в виде программы:
- начинаем вводить функцию Dj(w)
 ;
;
- применяем команду «Add Line» с панели «Programms» (рисунок Рисунок 4.20);
Рисунок 4.20
- на место первой строки вставляем «Dj1(w)», затем команду «if» с панели «Programms» (рисунок Рисунок 4.21), затем неравенство
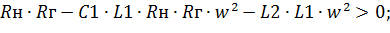
| (4.34) |
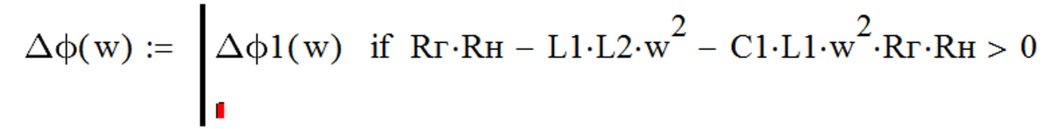
Рисунок 4.21
- на место второй строки вставляем «Dj1(w)+π», затем команду «otherwise» с панели «Programms» (рисунок Рисунок 4.22), затем неравенство
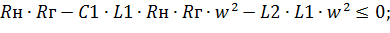
| (4.35) |
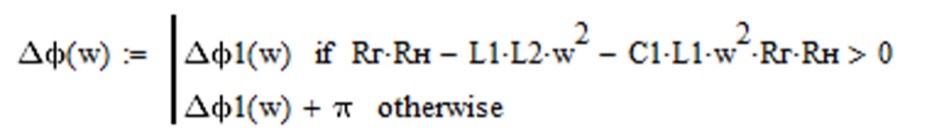
Рисунок 4.22
e) Для проверки корректности определения функции ФЧХ сравним в программе MathCad диаграммы функций аргумента (4.20) и (4.33) (рисунок Рисунок 4.23).
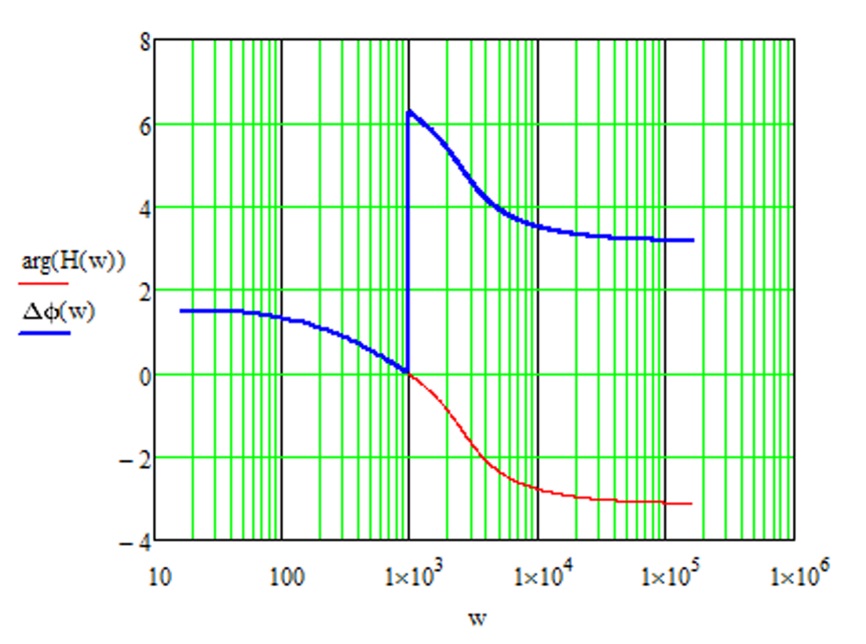
Рисунок 4.23 – Диаграмма аргумента КЧХ и ФЧХ
f) Отличие функции Dj(w) от arg(H(w)) после скачка на 2π (рисунок Рисунок 4.23) радиан ошибкой не является. Если изменить в выражении «Dj1(w)+π» второй строки функции Dj(w) знак «+» на «-», получиться абсолютное совпадение (рисунок Рисунок 4.24)
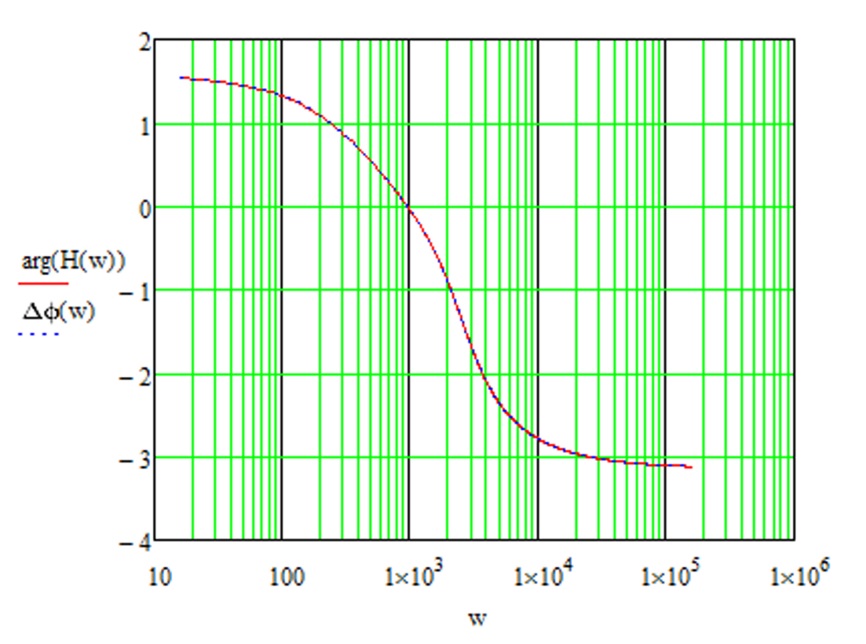
Рисунок 4.24 – Диаграмма аргумента КЧХ и ФЧХ
Дата добавления: 2016-12-27; просмотров: 2004;











