Расчёт спектра через коэффициенты обобщённого ряда Фурье

a) Для определения коэффициентов в рукопашную вычислить интегралы

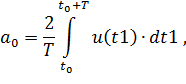
	(3.8)
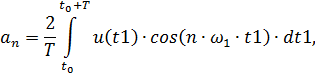
	(3.9)
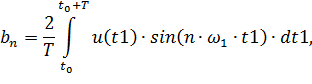
	(3.10)

где 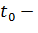произвольный момент начала интегрирования.

b) Постоянную составляющую, а также амплитуды и фазы первых N гармоник вычисляете с помощью выражений

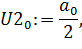
	(3.11)
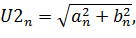
	(3.12)
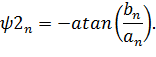
	(3.13)

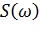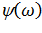c) Построить диаграммы амплитудного и фазового спектров. Тип линии диаграмм – «stem». Сравнить с диаграммами спектров и , а также с диаграммам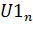и и 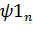. Если амплитудный спектр 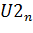отличается от 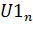– проверить вычисления пунктов a) и b) настоящего подраздела 3.4.

d) Построить временную диаграмму косинусоидального ряда Фурье

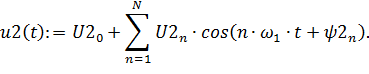
(3.14)

e) Если форма диаграммы качественно отличается от заданного сигнала – проверить вычисления пунктов a) – d) настоящего подраздела 3.4.

Расчёт операторной передаточной функции и частотных характеристик избирательной цепи

Задание на расчёт

На данном этапе выполняются следующие задачи:

a) заменить в заданной избирательной цепи реактивные элементы их операторными сопротивлениями. Любым удобным методом расчёта получить выражение для операторной передаточной функции 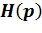. Упростить выражение до правильной двухэтажной дроби;

b) выполнив в полученной функции 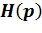замену p=j·ω, получить функцию комплексной частотной характеристики ;

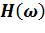c) на основе выражения 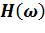в рукопашную вывести выражения для амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик 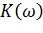и ;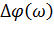

d) построить диаграммы вычисленных АЧХ и ФЧХ. Сравнив диаграммы АЧХ и любого из амплитудных спектров входного сигнала u(t) либо u_p(t), сделать качественное заключение о степени искажения выходного сигнала.