Для оценки свойств механических характеристик электропривода используют понятие жесткости характеристики. Жесткость определяется по выражению

,

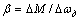где ∆М – изменение момента двигателя; ∆ω_д – соответствующее изменение угловой скорости.

Для линейных характеристик значение β остается постоянным, для нелинейных – зависит от рабочей точки.

Используя это понятие, характеристики, приведенные на рис. 5, можно качественно оценить так: 1 – абсолютно жесткая (β = ∞); 2 – жесткая; 3 – мягкая.

Уравнение движения электропривода. Статическая устойчивость электропривода

При воздействии на электропривод различных возмущений (изменение статического момента, колебания сетевого напряжения и т.п.) в нем возникают переходные процессы. Уравнение движения электропривода учитывает силы и моменты, действующие в переходных режимах.

Как известно из физики, в соответствии с законом Ньютона при поступательном движении движущая сила F уравновешивается силой сопротивления F_c и инерционной силой :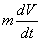

.

Для электропривода характерно вращательное движение, а уравнение его движения имеет аналогичный вид:

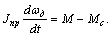(1.6)

Здесь аналогом массы является приведенный момент инерции J, вместо линейной скорости V рассматривается угловая скорость ω_д, а в правую часть уравнения входят момент двигателя Ми статический момент механизма М_с. Из уравнения (6) следует, что в установившемся режиме, когда ускорение ,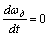

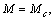(1.7)

т.е. момент двигателя уравновешивается моментом сопротивления производственного механизма. На рис. 1.6 показаны механические характеристики: 1 – двигателя и 2 – производственного механизма. (Фактически момент двигателя и момент М_с имеют противоположные знаки, но для удобства анализа их показывают в одном и том же квадранте). Очевидно, что равенству (1.7) соответствует на рис. 1.6 точка а, в которой характеристики пересекаются. При этом угловая скорость электропривода равна ω_д1.

Установившийся режим работы привода может быть устойчивым или неустойчивым. Для решения этого вопроса проанализируем поведение электропривода при отключениях от равновесного режима в точке а.

Предположим: под действием возмущения угловая скорость отклонилась относительно ω_д на +∆ω . В этом случае момент двигателя уменьшится и примет значение М₁(см. рис. 1.6), а статический момент возрастет до М_с1, т.е будет иметь место соотношение

.

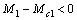При этом в соответствии с уравнением (1.6), ускорение станет отрицательным, т.е. привод замедлится, а ω_д снизится. Система будет стремиться возвратиться к положению равновесия в точку а, что условно показано на рис. 1.6 стрелками.

Рассмотрим теперь ситуацию, когда угловая скорость отклонится на - ∆ω: момент двигателя возрастет до М_2, а момент механизма снизится до М_с2, и будет выполняться соотношение

.

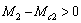Ускорение в этом случае станет положительным, угловая скорость ω_д возрастет и система вновь устремится к положению равновесия в точке а.

Проведенный анализ показывает, что режим работы электропривода в точке а для рассматриваемого сочетания характеристик двигателя и механизма будет устойчивым.

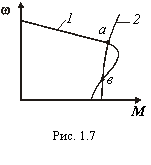
Условие устойчивости является совершенно необходимым условием работоспособности электропривода. Следует учитывать, что оно выполняется далеко не всегда. Предлагается самостоятельно провести аналогичный анализ для сочетания характеристик, показанных на рис. 1.7 (1 - характеристика двигателя, 2 - характеристика механизма), и убедиться, что в точке а условия устойчивости выполняются, а в точке в нет.

Выводы, получаемые в результате проведенного анализа, характеризуют так называемую статическую устойчивость электропривода, т.е. способность системы возвращаться к исходному режиму при достаточно «малых» отклонениях от положения равновесия.