Полученные выражения (2.3), (2.5) для характеристик двигателя представляют собой уравнение прямой. Они справедливы, если пренебречь реакцией якоря.
В уравнениях (2.3), (2.5) первое слагаемое представляет собой угловую скорость идеального холостого хода (при этом ток якоря и момент равны нулю):
ω0 = 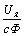 . (2.6)
. (2.6)
Второй член в этих уравнениях характеризует статическое падение угловой скорости от нагрузки:
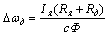 или
или 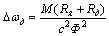 (2.7)
(2.7)
На рис. 2.3 падение скорости показано для номинального значения момента Mном (тока Iном). При неизменном магнитном потоке момент и ток якоря, как следует из соотношения (2.4), пропорциональны. Поэтому механическая и электромеханическая характеристики двигателя (см. рис. 2.3) отличаются только масштабом по оси ординат.
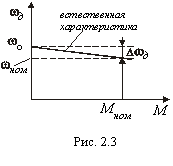
Характеристика, полученная при номинальном значении напряжения на якоре Uном, номинальном магнитном потоке Фном и отсутствии внешних резисторов в якорной цепи, называется естественной. Жесткость естественной характеристики определяется только сопротивлением якорной цепи двигателя:
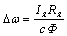 или
или 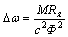 . (2.8)
. (2.8)
Снижение скорости ωд под нагрузкой объясняется следующим. При увеличении момента сопротивления механизма угловая скорость начинает снижаться. В результате уменьшается ЭДС E согласно (2.2). Ток якоря при этом, как следует из (2.1), увеличивается. Соответственно возрастает момент двигателя (см. уравнение (2.4)). Этот процесс продолжается до тех пор, пока момент двигателя не сравняется с моментом сопротивления. После достижения равенства М=Мс наступит новый установившийся режим с меньшей угловой скоростью ωд.
При инженерных расчетах коэффициенты, входящие в уравнения характеристик двигателя, могут быть определены через номинальные параметры двигателя, приводимые в каталогах. При номинальном магнитном потоке
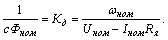 (2.9)
(2.9)
Здесь коэффициент Кд - коэффициент передачи двигателя, его размерность 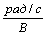 . С использованием этого понятия уравнения (14), (16) могут быть переписаны в виде:
. С использованием этого понятия уравнения (14), (16) могут быть переписаны в виде:
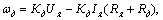 (2.10)
(2.10)
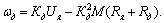 (2.11)
(2.11)
В этих уравнениях, как и в (14, 16), первый член представляет собой угловую скорость идеального холостого хода, а второй – падение скорости от нагрузки:
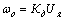 ;
; 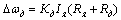 (2.12)
(2.12)
Или
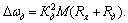 (2.13)
(2.13)
Пример. Известны номинальные данные двигателя:
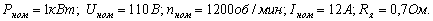
Дата добавления: 2016-12-27; просмотров: 1317;











