Удар тела о неподвижную преграду

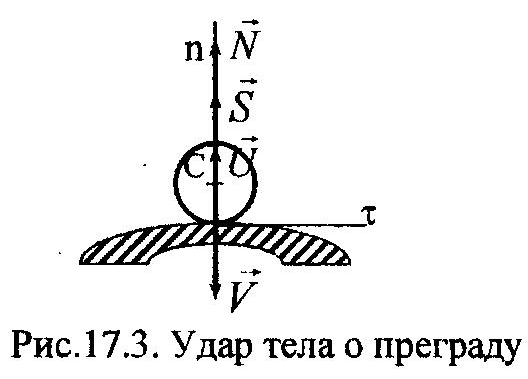
Рассмотрим прямой центральный удар шара о неподвижную поверхность (рис. 17.3). Центральным называется такой удар, при котором нормаль к точке касания проходит через центр масс тела. Для однородного шара это будет всегда. Пусть шар массой m ударяется о неподвижную поверхность со скоростью V. Определим величину ударного импульса, S, возникающего от ударной силы N – реакции поверхности

на шар (рис. 17.3). Воспользуемся для решения задачи выражением основного уравнения теории удара (17.2), спроектированного на нормаль n, получим:

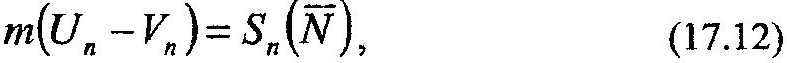
где U_n=U; V_n=-V; S_n(N)=Nτ; τ – время удара.

Согласно (17.9)

и тогда:

Из (17.14) видно, что ударный импульс зависит не только от скорости тела при столкновении, но и от его упругих свойств – коэффициента восстановления.

Теорема Карно

При соударении тел происходит потеря кинетической энергии. Наибольшая потеря будет иметь место при абсолютно неупругом ударе. Полагая, что тела до удара двигались поступательно, получим следующее выражение:

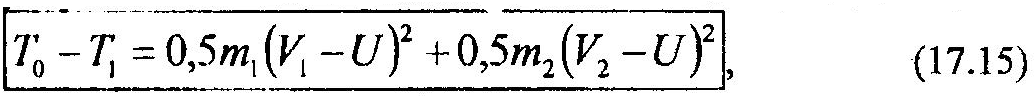
где Т₀, Т₁ – кинетическая энергия системы в начале и конце удара;

V_1, V₂, U – скорости тел в начале и после удара;

(V₁-U), (V₂-U)- потерянные при ударе скорости тел.

Теорема Карно: потеря кинетической энергии при абсолютно неупругом ударе равна