Ки тела изменяются на конечную величину.
Особенность данного явления заключается в том, что при действии обычных «неударных сил» за время удара скорости точек тела не изменяют своих значений. Действительно, согласно теоремы об изменении количества движения материальной точки, имеем:
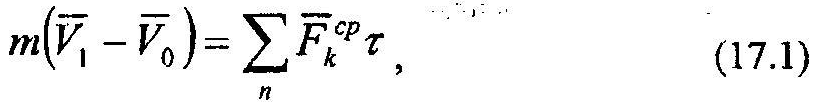
где V0,V1 – начальное и конечное значения скорости точки;
| τ – время удара; |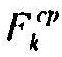 
| – среднее за время τ значение силы. |
Поскольку τ→0, постольку при обычных значения сил левая часть выражения (17.1) будет практически равна нулю, т.е.: V1=V0. Изменение величины скорости точки на конечную величину будет иметь место только при действии сил с модулем, F~1/τ. Такие силы называются ударными.
Т.к. значения ударных сил очень велики, в время удара мало, то возникает ситуация, когда пришлось бы оперировать при решении задач большим диапазоном порядков чисел. Это создает некоторые технические проблемы. Избежать это можно путем использования вместо сил их импульсов. Тогда выражение теоремы об изменении количества движения точки при ударе примет следующий вид:
где U, V – конечное и начальное значения скорости точки;
Sk – импульс ударной k-й силы.
Ясно, что импульсы неударных сил будут, практически, равны нулю, и поэтому в выражение (17.2) не входят.
Уравнение (17.2) является основным уравнением теории удара и имеет в этой области такое же значение, как и основной закон динамики в случае неударных сил. Согласно (17.2): изменение количества движения материальной точки за время удара равно геометрической сумме ударных импульсов, действующих на эту точку.
Поскольку τ→0 и, соответственно, перемещение точки за время удара практически равно нулю, т.е. Vсрτ→0, постольку можно считать, что изменение скорости точки происходит «на месте», при отсутствии ее перемещения.
Дата добавления: 2016-12-16; просмотров: 1198;
Поиск по сайту
Узнать еще
- D-технология построения чертежа. Типовые объемные тела: призма, цилиндр, конус, сфера, тор, клин. Построение тел выдавливанием и вращением. Разрезы, сечения.
- I.1.7 ДВИЖЕНИЕ ТЕЛА ПО ОКРУЖНОСТИ
- I.3. Антитела системы АВ0
- III. 4 МЕХАНИКА ТВЁРДОГО ТЕЛА
- IV этап – обособление тела зародыша
- VIII. Кровоснабжение, венозный и лимфатический отток, иннервация органов и частей тела
- Агрегаты регулирования потока рабочего тела по расходу и давлению
- Аморфные и кристаллические тела.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
