I.3.4 УДАР АБСОЛЮТНО УПРУГИХ И НЕУПРУГИХ ТЕЛ
Удар - изменение скоростей тел за очень малый промежуток времени их столкновения. При соударении, тела в большей либо меньшей мере деформируются. При этом кинетическая энергия тел переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Увеличение внутренней энергии приводит к нагреванию тел.
Явление удара разделяется на две стадии: в течение первой стадии, вследствие взаимной деформации, происходит сближение центров масс обоих тел, в течение второй стадии центры масс снова удаляются друг от друга. Если вторая стадия отсутствует, то удар будет неупругим; если в течение второй стадии деформация полностью исчезает, причём нет перехода механической энергии в теплоту, то удар будет абсолютно упругим. В действительности наблюдаются промежуточные случаи полуупругого удара. Большую роль играет при ударе то, являются ли поверхности соприкосновения гладкими или шероховатыми. В последнем случае скольжение тел к концу соударения исчезает. Удар называется центральным, если прямая, соединяющая центры масс, совпадает с общей нормалью к поверхностям обоих тел в точках их соприкосновения; в противном случае – удар нецентральный. Если тела до удара совсем не вращаются и движутся друг относительно друга только в направлении общей нормали, то удар называется прямым. В случае прямого удара трение не играет роли.
Рассмотрим два предельных случая:
§ абсолютно неупругий удар;
§ абсолютно упругий удар.
Абсолютно неупругим называется такой удар, при котором потенциальная энергия упругой деформации не возникает; кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. После удара тела движутся с одинаковой скоростью (т.е. как одно тело), либо покоятся. При таком ударе выполняется только закон сохранения импульса, закон сохранения механической энергии не соблюдается – механическая энергия частично или полностью переходит во внутреннюю.
Рассмотрим этот случай на примере удара абсолютно неупругих шаров. Два шара с массами 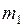 и
и 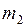 (рис. 31,а) двигаются в одном направлении со скоростями
(рис. 31,а) двигаются в одном направлении со скоростями 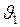 и
и 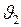 .
.

а)
б)
|
После взаимодействия (т.е. после абсолютно неупругого удара) оба шара будут двигаться с общей скоростью 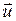 (рис.31, б). Применим к этой системе закон сохранения количества движения (закон сохранения импульса):
(рис.31, б). Применим к этой системе закон сохранения количества движения (закон сохранения импульса):
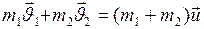
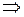
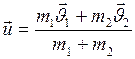 . (I.90)
. (I.90)
Следствия:
1. Скорость шаров 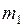 и
и 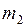 изменилась на величину
изменилась на величину 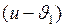 и
и 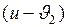 соответственно.
соответственно.
2. Если 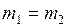 и
и 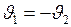 (шары идут навстречу друг другу), то
(шары идут навстречу друг другу), то 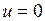 .
.
3. Если удар направлен в сторону неподвижного тела 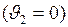 с большой массой (например, стена,
с большой массой (например, стена, 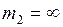 ), то
), то
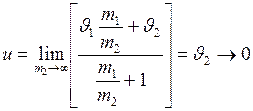 .
.
Как изменяется кинетическая энергия при неупругом ударе?
Перед столкновением энергия равна: 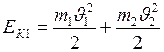 .
.
После столкновения 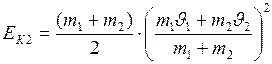 .
.
Убыль кинетической энергии за время столкновения:
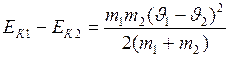 . (I.91)
. (I.91)
Итак, кинетическая энергия сохраняется в отсутствии какого-либо столкновения, т.е. когда скорости совпадают 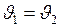 и шары движутся в одном направлении. Но если скорости
и шары движутся в одном направлении. Но если скорости 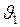 и
и 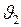 различны, то кинетическая энергия убывает, производя при этом работу деформации и превращаясь в теплоту.
различны, то кинетическая энергия убывает, производя при этом работу деформации и превращаясь в теплоту.
Абсолютно упругим называется такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкиваясь, друг от друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, определяемыми двумя условиями – сохранением суммарной энергии и суммарного импульса тел.
Мы ограничимся рассмотрением центрального удара двух однородных шаров, т.е. когда скорости тел до удара направлены вдоль линии, соединяющей центры масс этих тел.
Два шара с массами 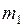 и
и 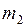 движутся поступательно вдоль горизонтальной прямой со скоростями
движутся поступательно вдоль горизонтальной прямой со скоростями 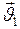 и
и 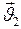 (рис.32, а). Требуется определить скорости шаров
(рис.32, а). Требуется определить скорости шаров 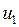 и
и 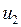 . Пусть скорости шаров
. Пусть скорости шаров 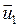 и
и 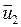 после удара ориентированы так, как показано на рисунке 32,б.
после удара ориентированы так, как показано на рисунке 32,б.
При выбранной ориентации заданных векторов 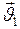 ,
, 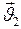 и оси
и оси 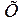 имеем
имеем
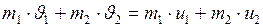 . (I.92)
. (I.92)
а)

б)
|
Система шаров консервативна, и поэтому к ней применим закон сохранения механической энергии в виде
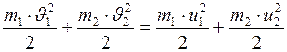 , (I.93)
, (I.93)
так как потенциальная энергия шаров в поле тяготения Земли при движении по горизонтали не изменяется.
Решая совместно уравнения (I.92) и (I.93), находим скорости 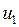 и
и 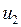 , которые тела имеют после абсолютного удара,
, которые тела имеют после абсолютного удара,
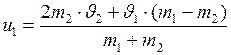 ;
; 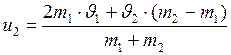 . (I.94)
. (I.94)
Следствия:
1. Если массы тел равны 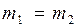 , то
, то 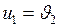 и
и 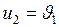 , - тела обменялись скоростями.
, - тела обменялись скоростями.
2. Если второй шар до удара покоился 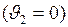 , то
, то
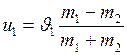 ;
; 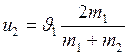 (I.95)
(I.95)
а) при 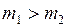 первый шар после удара будет продолжать двигаться вправо, но с меньшей скоростью.
первый шар после удара будет продолжать двигаться вправо, но с меньшей скоростью.
б) при 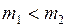 первый шар будет двигаться влево. Второй шар в обоих случаях после удара будет двигаться вправо.
первый шар будет двигаться влево. Второй шар в обоих случаях после удара будет двигаться вправо.
3. Если при 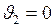 будет выполняться условие
будет выполняться условие 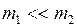 , то
, то 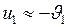 и
и 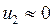 .
.
Лёгкое тело после абсолютно упругого удара о массивное неподвижное тело будет изменять направление вектора скорости на противоположное.
Дата добавления: 2016-09-06; просмотров: 4210;











