Общие теоремы динамики при ударе

В теории удара не все рассмотренные ранее общие теоремы динамики можно использовать в том же виде, в котором они были получены применительно к неударным силам. Остановимся на наиболее важных теоремах.

1. Теорема об изменении количества движения механической системы

Выражение (14.24), полученное при рассмотрении данной теоремы применительно к неударным силам, остается без изменений и для ударных сил:

Поскольку неударные силы за время удара изменить скорость точек не могут, постольку в правой части (17.3) рассматривают только импульсы ударных сил, т.е.: изменение количества движения механической системы за время удара равно геометрической сумме ударных импульсов, действующих на систему.

Выражение (14.24) и (17.3) представляют собой интегральную форму записи данной теоремы. Следует отметить, что выражение теоремы в дифференциальном виде (14.21) в теории удара не используется, т.к. в его правой части находятся ударные силы.

Закон сохраненияколичества движения механической системы в теории удара

формулируется аналогично условиям воздействия обычных сил, т.е.: если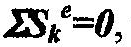

то

Q=const. Это означает, что внутренние ударные силы изменить количество движения механической системы не могут.

2. Теорема об изменении кинетического момента механической системы

Данная теорема в теории удара принимает несколько иной вид. Это связано с тем, что при ударе точки системы не имеют перемещений.

Для получения искомого выражения воспользуемся основным уравнением теории удара (17.2) и запишем его для k-й точки механической системы:

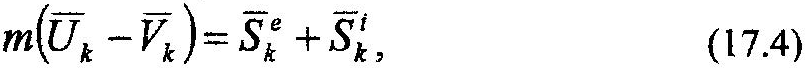
где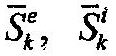

– главные векторы импульсов ударных внешних и внутренних

сил, приложенных к k-й точке системы;

или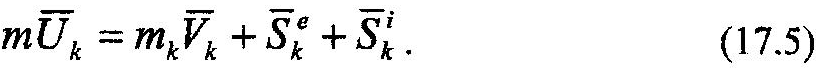

Следует заметить, что все векторы уравнения (17.5) приложены к неподвижной точке системы, т.к. во время удара точки не перемещаются. Рассматривая вектор, стоящий в левой части (17.5) как равнодействующую трех векторов, находящихся справа от знака равенства, можно записать выражение теоремы Вариньона относительно какого-либо центра О, справедливой для любых векторных величин:

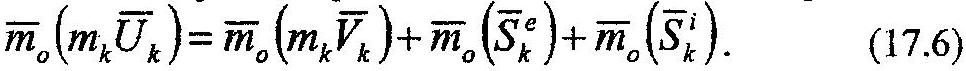
Рассуждая подобным образом, можно для каждой точки механической системы записать аналогичные выражения, получив тем самым систему n уравнений вида (17.6). Сложив почленно эти уравнения, получим:

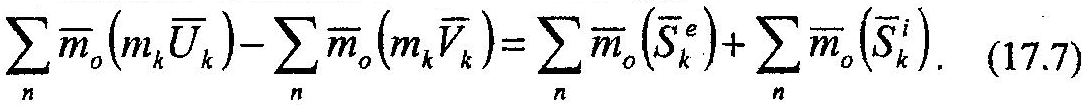
Учитывая, что в левой части (17.7) находятся выражения кинетических моментов механической системы в конечный и начальный моменты времени, соответственно, а последнее слагаемое в правой части равно нулю, на основе 2-го свойства внутренних сил механической системы, выражение (17.7) перепишем в следующем виде:

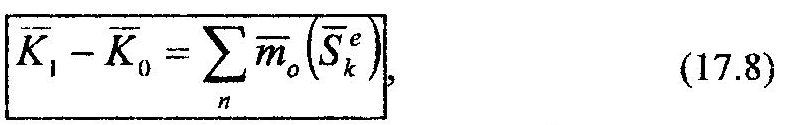
т.е.: изменение кинетического момента механической системы за время удара равно