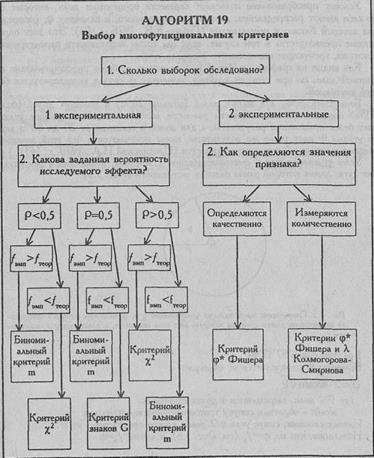
Алгоритм выбора многофункциональных критериев

5.7. Математическое сопровождение к описанию критерияφ* Фишера

Угловое преобразование позволяет перевести процентные доли, которые сами по себе имеют распределение, далекое от нормального, в величину φ, распределе­ние которой близко к нормальному (Гублер Е.В., 1978, с. 84). Это дает опреде­ленные преимущества в том случае, если мы хотим использовать параметрические критерии, требующие нормальности распределений.

Как видно из графика на Рис. 5.1, φ нарастает в общем пропорционально про­центной доле, но при этом на крайних значениях φ кривая характеризуется боль­шей крутизной.

Благодаря этому для малых долей (меньше 20%) и больших долей (больше 80%) определение достоверности разности долей по соответствующим углам φ дает более правильные результаты, а для долей в пределах от 20 до 80% замена их углами φ дает такие же результаты, какие получаются и без этой замены, но техника вычислений при этом упрощается (Плохинский Н.А., 1970, с. 143).

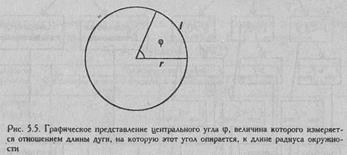
Углы φ измеряются в радианах. Радиан - это угол, являющийся центральным для дуги, длина которой равна радиусу окружности (Рис. 5.5).

1 радиан равен 57°17'44".

Величина φ определяется по формуле:

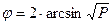
где Р - доля, выраженная в долях единицы;

arcsin - обратная синусу тригонометрическая функция.

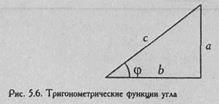
Иными словами, синус угла φ/2 равен корню квадратному из Р. Напомним, что sinφ=^а/_с (см. Рис. 5.6), a arcsin ^а/_с= φ

Величину φ можно вычислить в радианах или определить по специальной таб­лице (Табл. XII Приложения 1).

Н.А. Плохинский использует иную формулу определения ф:

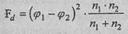
где φ₁ - значение угла для первой доли;

φ₂- значение угла для второй доли;

n₁ - количество наблюдений в первой выборке;

n₂ - количество наблюдений во второй выборке.

Эмпирические значения F_d сопоставляются с критическими значениями крите­рия F Фишера, которые определяются по таблице для степеней свободы v₁ и v₂, определяемых как:

По нашему опыту, этот вариант критерия с использованием углового преобра­зования дает менее точные результаты, чем вариант Е.В. Гублера (1978).

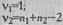
[1] Определения и формулы расчета М и СТ даны в параграфе "Распределение при­знака. Параметры распределения".

[2] О нормальном распределении см. Пояснения в п. 1.3.

[3] Определение и описание непараметрических критериев дано ниже в данной главе.

[4] О понятии мощности критерия см. ниже.

[5] с - количество выборок.

[6] Для крайнего правого столбца S₁ не указываются, поскольку они равны нулю.

[7] Сдвиг - это разность между вторым и первым замерами. Сначала вычисляются разности отдельно для каждой из групп, а уж затем проводятся сопоставления двух рядов разностей (сдвигов), полученных в разных группах. Примером такого сопоставления сдвигов в ощущении психологической дистанции является Задача 1.

[8] Критерий знаков с математической точки зрения является частным случаем би­номиального критерий для двух равновероятных альтернатив. При вероятности каждой из альтернатив P=Q=0,50 критерий знаков является зеркальным отраже­нием биномиального критерия (см. параграф 5.3). В некоторых руководствах кри­терий знаков называют критерием Мак-Немара (McCall R., 1970; Рунион Р., 1982).

[9] Можно вычитать значения "после" из значений "до", это никак не повлияет на расчет критерия. Но лучше во всех случаях придерживаться одной системы, чтобы не запутаться самим.

[10] *Испытуемый Л-в так и не смог правильно решить анаграмму 2. |4 Е. В. Сидоренко

[11] На самом деле области применения критерия %² многообразны (см., например: Суходольский Г.В., 1972, с. 295), но в данном руководстве мы ограничиваемся только этими двумя, наиболее часто встречающимися на практике, целями.

[12] Доброхотова Т. А., Брагина Н. Н. Левши. М.: "Книга", 1994.

[13] Гистограмма - это диаграмма, в которой различная величина частот изображается различной высотой столбиков (Плохинский Н. А., 1970, с. 14.)

[14] Все приведенные эмпирические частоты на самом деле пропорциональны количе­ству благосклонных высказываний невесты о женихах в тексте пьесы.

[15] Поправка на непрерывность при ν=l предназначена для корректировки несоот­ветствия между дискретным биномиальным распределением и непрерывным рас пределением (Рунион Р., 1982, с. 39.)

[16] Социальный атом "... состоит из всех отношений между человеком и окружающими его людьми, которые в данный момент тем или иным образом с ним связаны" (Moreno J. L., 1951.)

[17] Целесообразно было бы проверить совпадение распределения ошибок в обеих выборках с распределением Пуассона. Закону Пуассона подчиняются распределе­ния редких событий, приходящихся 0, 1, 2,... раз на сотни и тысячи наблюдений. Однако в данном случае эта модель неприменима: средняя и дисперсия не равны друг другу и составляют, соответственно, 0,91 и 1,96 в первой выборке и 2,29 и 5,43 во второй выборке.

[18] Относительная частота, или частость, - это частота, отнесенная к общему коли­честву наблюдений; в данном случае это частота попадания желтого цвета на дан-позицию, отнесенная к количеству испытуемых. Например, частота попадания желтого цвета на 1-ю позицию f=24; количество испытуемых n=102; относительная а f*=f /n=0,235.

[19] Все формулы приведены для дискретных признаков, которые могут быть выра­жены целыми числами, например: порядковый номер, количество испытуемых, ко­личественный состав группы и т.п.

[20] Психологическое поглаживание - это "...любой акт, предполагающий признание присутствия другого человека" (Берн Э., 1992, с. 10). Практически в транзактно-аналитических сессиях под поглаживанием понимается выражение симпатии, вос­хищения, одобрения, любое искреннее признание положительных качеств и прояв­лений другого человека, к которым могут относиться внешние данные, глубинные личностные свойства, мастерство в своем деле, способность дарить психологическое тепло, и вовремя произнесенное слово и т.д.

[21] FPI-R - Фрайбургский личностный опросник

[22] В первоначальной выборке было 50 человек, но 8 из них были исключены из рассмотрения как имеющие средний балл по показателю анергии вытеснения (14-15). Показатели интенсивности чувства недостаточности у них тоже средние: 6 значений по 20 баллов и 2 значения по 25 баллов.

[23] Поправка на непрерывность вносится во всех случаях, когда признак принимает всего два значения и число степеней свободы поэтому равно 1 (см. параграф 4.2)

[24] В принципе признак может принимать и большее количество значений, так как любую шкалу, как мы убедились, можно свести к альтернативной шкале "Есть эффект" - "Нет эффекта".