Автоматна модель шифратору

Відправним пунктом для детальних досліджень криптосистем нерідко виступають їх моделі у вигляді так званих кінцевих автоматів. Наукова дисципліна «Теорія автоматів» вивчає проблеми аналізу та синтезу автоматів – деяких абстрактних математичних об’єктів ‑ послідовних автоматів (автоматів с пам’яттю) що функціонують за певними правилами [1]. Зупинимося на деяких аспектах застосування автоматного підходу для вивчення проблем криптографічного захисту інформації.

Кінцевим послідовним автоматом або автоматом Мілі називається система з п’яти елементів [1]:

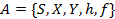, (1)

де 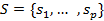– множина внутрішніх станів; 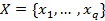– множина вхідних сигналів або вхідний алфавіт); 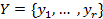– множина вихідних сигналів або вихідний алфавіт; відображення 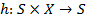– функція переходів; 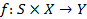– функція виходів. За необхідності система (1) може включати шостий елемент 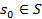– початковий стан автомату.

Вважається, що автомат змінює свої стани в дискретні моменти часу, що отримали назву такти: 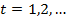. Якщо в момент часу 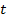автомат 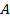перебуває у стані 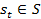та спостерігає на вході сигнал 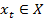, то він формує вихідний сигнал 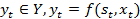змінює свій внутрішній стан .

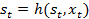Таким чином, автомат S, що перебуває у початковому стані 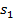, породжує автоматне відображення 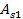, яке перетворює вхідну послідовність ‑ слово 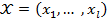в вихідне слово 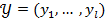. При цьому спостерігається послідовність внутрішніх станів автомату .

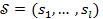В автоматі Мура на відміну від автомату Мілі функція виходів не залежить від вхідної послідовності, тому ця модель може бути корисною для аналізу шифратору, що формує «чисті» шифруючи послідовності.

1. Модель Мили (или автомат Мили): ½ at+1 = δ(at , xt); yt = λ(at , xt). (2)

2. Модель Мура (или автомат Мура): ½ at+1 = δ(at , xt); yt = λ(at). (3)

Для задания автоматов удобно использовать табличное представление (см. табл. 1, 2, 3). Таблица 1. Таблица переходов автомата Мили a1 . . . ap x1 δ(a1, x1) . . . δ(ap, x1) . . . . . . . . . . . . xn δ(a1, xn) . . . δ(ap, xn) Таблица 2. Таблица выходов автомата Мили a1 . . . ap x1 λ(a1, x1) . . . λ(ap, x1) . . . . . . . . . . . . xn λ(a1, xn) . . . λ(ap, xn) Таблица 3. Таблица переходов автомата Мура λ(a1) . . . λ(ap) a1 . . . ap x1 δ(a1, x1) . . . δ(ap, x1) . . . . . . . . . . . . xn δ(a1, xn) . . . δ(ap, xn) На множестве состояний автомата определим отношение эквивалнтности: ai ∼ aj , если ∀ξ ∈ X∗ (X∗ – множество всевозможных слов над алфавитом X) выполняется равенство: Sai (ξ) = Saj (ξ). Объединяя состояния автомата в классы эквивалентности, можно перейти к автомату, эквивалентному исходно- му, с минимально возможным числом состояний [3]. Далее будем рассматривать минимизированные последовательные автоматы. 2. Автоматная модель шифратора Следуя [2], построим модель шифрующего автомата. Для этого необходимо дать несколько определений.

Шифром (или криптосистемой) называется система из пяти элементов Σ = (K, Xe∗ , Ye∗ , E, D), (4) где K – множество ключей; Xe∗ ⊆ X∗ – множество открытых текстов; Ye∗ ⊆ Y ∗ – множество закрытых текстов; Ek : ξ → ψ (ξ ∈ Xe∗ , ψ ∈ Ye∗ ) – правило зашифрования для k ∈ K; Dk : ψ → ξ – правило расшифрования для k ∈ K. При этом должны выполняться следующие свойства: 1. ∀ξ ∈ Xe∗ , ∀k ∈ K: Dk(Ek(ξ)) = ξ (отсюда следует, что отображение Ek инъективно). 2. Ye∗ = S Ek(ξ), где объединение берется по всем k ∈ K и ξ ∈ Xe∗ . Очевидно, что функции переходов и выходов автомата, моделирующего ра- боту шифра, должны зависить от ключа k. В качестве такого шифрующего автомата можно рассмотреть следующую систему: S = (A × K, X, Y, δ, λ), (5) функциональная модель которой представляется автоматом Мили: ½ δ((at , k), xt) = δk(at , xt) = (at+1, k); λ((at , k), xt) = λk(at , xt) = yt . (6) Перейдем теперь к вопросам расшифрования. С точки зрения автоматной модели для этого необходимо построить обратный автомат или, более строго, обратить автоматное отображение. Автомат S −1 = (A, Y, X, e δ, e λe) называется обратным (слева) к автомату S = (A, X, Y, δ, λ), если ∀a ∈ A ∃ea ∈ Ae такое, что ∀ξ ∈ X∗ выполняется равен- ство S −1 ea (Sa(ξ)) = ξ. Далее, пока не оговорено противное, будем рассматривать левую обратимость. Очевидно, что для существования обратного автомата необходимо и доста- точно потребовать инъективность автоматного отображения Sa для любого на- чального состояния a. Инъективность автоматного отображения достигается требованием инъективности функции выходов λ при фиксированном состоя- нии a, то есть частичной функции λa : X → Y . Это, в свою очередь, означает, что |λ −1 a (y)| ≤ 1 [2]. Итак, для однозначности расшифрования на шифрующий автомат (5), (6) необходимо наложить условие инъективности частичной функции выходов λa. Инъективность λa приводит к следующему алгоритму построения обратного автомата [2]: 1. Если |λ −1 a (y)| = 1, то λe(a, y) = λ −1 a (y) и δe(a, y) = δ(a, λ−1 a (y)). 2. В противном случае, когда |λ −1 a (y)| = 0, λe(a, y) – произвольный x ∈ X, δe(a, y) – произвольное a ∈ A. 114 Если мощности алфавитов X и Y совпадают, то обратный автомат строится однозначно. В общем случае должно выполняться |X| 6 |Y |. Если неравенство строгое, то обратный автомат является частичным. Заметим, что для обратимости автомата необходимо и достаточно, чтобы в его табличном представлении в каждом столбце таблицы выходов все выходные сигналы были различны.

Для иллюстрации предложенных алгоритмов и моделей рассмотрим автомат Мили S, заданный таблицами 4, 5. Если произвольное значение сигнала или состояния обозначить прочерком, то автомат S −1 представляется таблица- ми 6, 7. Таблица 4. Переходы автомата S a1 a2 a3 x1 a3 a1 a1 x2 a1 a3 a2 Таблица 5. Выходы автомата S a1 a2 a3 x1 y3 y1 y2 x2 y1 y3 y1 Таблица 6. Переходы автомата S −1 a1 a2 a3 y1 a1 a1 a2 y2 − − a1 y3 a3 a3 − Таблица 7. Выходы автомата S −1 a1 a2 a3 y1 x2 x1 x2 y2 − − x1 y3 x1 x2 − В простейшем случае ключом можно считать сам автомат. Пусть a3 – на- чальное состояние. В качестве открытого текста рассмотрим последователь- ность ξ = x1x1x2x1x1. Тогда закрытый текст ψ = Sa3 (ξ) очевидным образом определяется по таблицам 4, 5: ξ = x1 x1 x2 x1 x1 α = a3 a1 a3 a2 a1 a3 ψ = y2 y3 y1 y1 y3 Процесс расшифрования проводится по таблицам 6, 7: ψ = y2 y3 y1 y1 y3 α = a3 a1 a3 a2 a1 a3 ξ = x1 x1 x2 x1 x1

Далее сформулируем ряд замечаний. Одним из преимуществ представленного «автоматного» способа шифрова- ния является то, что одинаковые фрагменты входной последовательности в общем случае шифруются различными блоками. Это видно даже на нашем при- мере: подпоследовательность x1x1 встречается во входном слове дважды, и ей соответствуют подпоследовательности y2y3 и y1y3 закрытого текста.

Если потребовать, чтобы частичная функция λx также была инъективной, то таблица выходов автомата (без строки состояний и столбца входных сигна- лов) будет представлять собой латинский прямоугольник – элементы в линиях (как в столбцах, так и в строках) не повторяются. Существующие оценки числа латинских прямоугольников [9] могут служить основой для анализа крипто- стойкости алгоритмов «автоматного» шифрования. Следует отметить, что итогом теоретико-автоматной модели шифра является принципиальная возможность построения криптосистемы в виде двух последовательных автоматов (шифратора и дешифратора), блоки памяти которых совпадают [2].

3. Криптосистемы с открытым ключом, основанные на последовательных автоматах Идея использования автоматой модели в криптографии с открытым ключом не нова. Так, в Китае с 80-х годов прошлого века ведутся работы в области создания асимметричных криптосистем, основанных на конечных автоматах [11]. Здесь следует остановиться на терминологии. Конечный автомат - это модель распознавателя, являющаяся эквивалентом автоматной грамматики относительно порождаемых языков [4,10].

С точи зрения классической теории авто- матов, в частности последовательных абстрактных моделей, конечный автомат - это автомат Мура, в общем случае частичный, выходные сигналы которого заданы в алфавите {0, 1} [4].

В работе [8] предложена криптосистема с открытым ключом, основным элементом которой явлется последователный автомат. Как уже отмечалось, произвольный последовательный автомат S реализует автоматное отображение S(ξ) = ψ. При этом и входное, и выходное слова имеют одинаковую длину: |ξ| = |ψ|. Автомат S −1 с входным алфавитом Y и выходным алфавитом X, перево- дящий выходное слово ψ обратно во входное ξ, – это, как и ранее, обратный автомат, но теперь нам понадобится обратимость справа. Автомат S −1 = (A, Y, X, e δ, e λe) называется обратным (справа) к автомату S = (A, X, Y, δ, λ), если ∀a ∈ A ∃ea ∈ Ae такое, что ∀ψ ∈ Y ∗ выполняется ра- венство Sa(S −1 ea (ψ)) = ψ. Отметим, что для доказательства правой обратимости необходимо и достаточно потребовать, чтобы автоматное отображение Sa было сюръективным для любого начального состояния a, или предъявить эквива- лентное требование – сюръективность частичной функции выходов λa [2]. В табличном представлении автомата для правой обратимости необходимо и до- статочно, чтобы в каждом столбце таблицы выходов каждый выходной сигнал встречался как минимум один раз. Алгоритм построения правого обратного автомата достаточно прост [2]: λe(a, y) = x и δe(a, y) = δ(a, x), где x – произвольный элемент из множества λ −1 a (y), которое в силу сюръективности не пусто. Определим теперь инверсию с задержкой z, где z – некоторое натуральное число. Пусть ψ = S(ξ). Инверсия с задержкой S −1 z , получая на входе слово ψµ, 116 где µ – произвольное слово длины z, порождает на выходе слово νξ, где ν – также слово длины z. Представленная в [8] криптосистема с открытым ключом строится следую- щим образом. В качестве ключа зашифрования открываются z и S −1 z , а S хра- нится как секретный ключ расшифрования. Зашифрование исходного текста ψ происходит с помощью выбора произвольного слова µ длины z и применения автомата S −1 z к слову ψµ. При pасшифровании криптотекста легальный полу- чатель игнорирует первые z букв и применяет автомат S к оставшемуся слову. Отметим, что в данном методе используется правая инверсия с задержкой. Обсуждаемый в [6] асимметричный алгоритм шифрования также основан на паре автоматов S и S −1 z . На шифрующий автомат S накладывается требова- ние отсутствия инъективности частичной функции выходов λa (тогда автомат S необратим слева). При дополнительных условиях возможно построение левой инверсии с задержкой S −1 z , что в общем случае является трудной задачей.

Знание особенностей структуры автомата S дает легкий алгоритм получения S −1 z (секретный ключ).

4. Шифрование с помощью «раскрашивания» на автоматах Мура Достаточно много криптосистем используют подход, который может быть сфор- мулирован как шифрование с помощью «раскрашивания» [8]. «Краска» связы- вается с каждой буквой исходного текста. Для простоты будем полагать, что исходные тексты являются двоичными последовательностями. Тогда нам необ- ходимы только две краски - белая (бит «0») и черная (бит «1»). Ключ зашифрования должен давать метод, который порождает произволь- но много элементов, раскрашенных белой краской, и произвольно много элемен- тов, раскрашенных черной краской. Примером таких элементов могут являться слова некоторого фиксированного алфавита. Биты шифруются как слова, pас- кpашенные соответствующим обpазом. Для различных появлений бита «0» (со- ответственно «1») должны выбираться различные слова, раскрашенные белой (соответственно черной) краской. Для генерации «белых» и «черных» слов представляется возможным ис- пользовать автоматную модель. Пусть S = (A, X, Y, δ, λ, aн.с.) – автомат Мура, в котором выходной алфавит является двоичным: Y = {0, 1} и aн.с. – начальное состояние. Процесс зашифрования открытого двоичного текста заключается в следу- ющем. Текущий бит i (i ∈ {0, 1}) шифруется на автомате S как произвольное входное слово ξ алфавита X с тем ограничением, что последний символ вы- ходного слова ψ = S(ξ) равен «i». Следует отметить, что в автомате Мура, в отличие от модели Мили, выходное слово строится со сдвигом на один такт, то есть не учитывается выходной сигнал, приписанный начальному состоянию. При расшифровании текущее слово ξ криптотекста подается на вход авто- мата S: последний символ выходного слова ψ = S(ξ) и будет являться искомой «краской».

Однозначность расшифрования очевидна. Естественно, что сам ав- томат S необходимо держать в секрете. Таблица 8. Переходы автомата Мура S 1 0 1 0 1 a1 a2 a3 a4 a5 a a4 a4 a1 a2 a2 b a1 a1 a5 a3 a1 c a2 a1 a3 a5 a4 Рассмотрим предложенный способ шифрования на примере. Пусть автомат Мура S задан таблицей 8 и в качестве начального состояния выбрано состоя- ние a1. Зашифруем последовательность «00101». Одним из вариантов закры- того текста является последовательность слов: «a bc b c ab». Расшифрование продемонстрируем на примере слова «ab»: ξ = a b α = a1 a4 a3 ψ = 0 1 Так как последний символ выходного слова равен «1», то и соответствующий бит открытого текста – это единица. Очевидно, что все криптосистемы, основанные на шифровании с помощью раскрашивания, имеют тенденцию к недопустимо большому росту длины крип- тотекста, так как чем больше различных слов, пригодных для шифрования одного бита (а следовательно, чем больше длина каждого слова), тем более стойким является криптоалгоритм. Этот недостаток не столь существенен, если подобные криптосистемы ис- пользовать не для шифрования сообщений, а для шифрования ключей неко- торого симметричного алгоритма, который в дальнейшем и будет применяться для передачи сообщений [11]. По этой же причине шифрование с помощью раскрашивания наиболее ши- роко используется в асимметричных криптосистемах. Открытый ключ зашиф- рования – это метод выбора слов, сопоставимых каждому биту. В идеальной ситуации задача определения «краски» для заданного слова является трудно- решаемой, в то время как знание секретного ключа позволяет легко решать задачу расшифрования [8]. Рассмотренный алгоритм шифрования также может быть преобразован в криптосистему с открытым ключом. Как уже отмечалось, автомат Мура с дво- ичным выходным алфавитом является конечным автоматом. Пусть дан автомат Мура S 0 = (A, X, Y = {0, 1}, δ, λ0 , aн.с.). Это конечный ав- томат, определяющий автоматный язык L(S 0 ) – множество таких слов входного алфавита X, что последний символ соответствующих выходных слов равен «1». Построим автомат S 1 = (A, X, Y, δ, λ1 , aн.с.) по правилу: λ 1 (a, x) = λ 0 (a, x). Этот автомат задает автоматный язык L(S 1 ). 118 Согласно [8], выберем две грамматики Γ 0 и Γ 1 с одним и тем же терми- нальным алфавитом X так, чтобы языки L(Γ0 ) и L(Γ1 ), порождаемые этими грамматиками, удовлетворяли условию: L(Γi ) ∩ L(S i ) 6= ∅ (i ∈ {0, 1}). Построим две новые грамматики Γe0 и Γe1 такие, что L(Γei ) = L(Γi ) ∩ L(S i ) (i ∈ {0, 1}). Построение пересечения языков – стандартное. Отметим лишь, что в общем случае языки не замкнуты относительно операции пересечения, то есть тип результирующего языка в иерархии Хомского может быть произволь- ным [10]. Пара (Γe0 , Γe1 ) открывается в качестве ключа зашифрования – бит i шифру- ется как произвольное слово в L(Γei ) (i ∈ {0, 1}). Автоматы S 0 и S 1 хранятся в качестве секретного ключа. Перехватчик для расшифрования должен определить принадлежность каж- дого слова криптотекста языку L(Γei ) (i ∈ {0, 1}), то есть решить задачу распо- знавания, являющуюся трудной для произвольного контекстного языка, а для языка типа 0 – в общем случае неразрешимой. Легальный получатель решает легкую задачу принадлежности слова крип- тотекста одному из автоматных языков L(S 0 ) или L(S 1 ). В силу построения автоматов S 0 и S 1 , языки L(S 0 ) и L(S 1 ) не пересекаются (они являются дополнениями друг друга) [8, 10]. Тем самым расшифрование всегда будет однозначным. Рассмотренные в статье криптосистемы не являются единственно возмож- ной сферой применения «автоматного» подхода в криптографии. Автоматные модели используются в формальном анализе криптографиче- ских протоколов. Существующие алгоритмы основаны на следующем подходе. Если предположить, что злоумышленник может удалять сообщения из канала связи и помещать в канал связи созданные им сообщения, то любое сообще- ние, посланное легальным пользователем, можно рассматривать как сообще- ние, отправленное злоумышленнику, и любое сообщение, принятое легальным пользователем, как сообщение, полученное от злоумышленника. Тогда систему можно интерпретировать как автомат, используемый злоумышленником для генерации слов [5]. Представляет интерес идея построения однонаправленных хэш-функций на основе последовательных автоматов. Основное свойство однонаправленной функ- ции – простота вычисления и сложность (практическая невозможность) инвер- тирования. Тогда в качестве такой функции можно рассмотреть необратимое (или трудно обратимое) автоматное отображение. Требования на хэш-функцию накладывают ограничения и на «однонаправленный» автомат S: трудно подо- брать два разлиных входных слова ξ1 и ξ2 таких, что S(ξ1) = S(ξ2), а изменение одного символа во входном слове ξ ведет к изменению в среднем половины символов выходного слова ψ = S(ξ). В работах [6, 7] рассматриваются автоматные однонаправленные отображе- ния, для которых сложность построения обратного автомата приближается к экспоненциальной зависимости.

В заключение отметим, что для представленных в обзоре криптосистем не обсуждались такие вопрсы, как оценка сложности, область применения, сопо- ставимость с другими шифрами. Важно было показать принципиальную воз- можность приложения классических теоретико-автоматных моделей к задачам криптографии.

У більшості випадків сучасні шифратори є автономними автоматами Мура 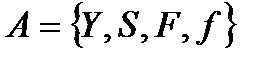, для яких 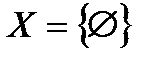, 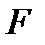: 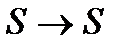; 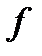: 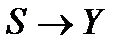, а переходи та виходи задаються у вигляді:

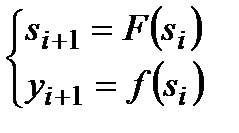, (2)

де ; .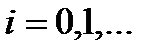

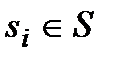У зв’язку з постійним зростанням швидкості передачі інформації шифри багатоалфавітної заміни у сучасних шифраторах практично не використовують. Тому у більшості випадків рівняння шифрування має вигляд:

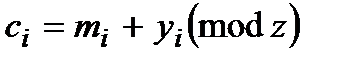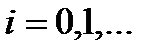; , (3)

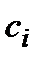де та 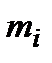– відповідно символи відкритого та шифрованого повідомлень;

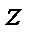– модуль алфавіту повідомлень;

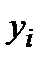– шифруюча гама.

Без обмеження загальних підходів для спрощення окремих викладень та пояснень подальший розгляд будемо вести навколо двійкових автоматів. Тому далі розглянемо двійкові автономні автомати Мура, для яких множина виходів 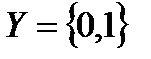, а множина станів 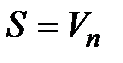– простір векторів довжини 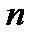. Умовну схему такого автомату, що описаний системою рівнянь (3), наведено на рис. 7.

. . .

{mi}

Блок ЛРРЗ що формує вектор стану Si

F

f

{ki}

J1 ... Jn

I1 ... Ir

{ci}

Управління рухом ЛРРЗ

Рис.7 Схема двійкового автомату Мура

Заключна частина

Формування якісної с криптографічної точки зору послідовності фактично еквівалентно задачі побудови надійного криптографічного алгоритму, оскільки в обох випадках виникає поняття однобічної функції, яку легко розрахувати, але досить складно обернути.

Оскільки безпека криптографічного захисту інформації базується на секретності ключу, це потребує від дослідників, розробників, виробників та користувачів засобів та систем КЗІ постійного вдосконалення рівня спеціальної підготовки та врахування останніх наукових досліджень повсякденній діяльності.