III.Акустические основы настройки музыкальных инструментов
1. Музыкальные строи современной европейской музыки
Под настройкой понимают установление высотного согласования между тонами интервалов музыкального инструмента. Цель настройки — получение либо чисто настроенных интервалов (чистый строй), либо интервалов с определенной расстройкой (например, равномерно-темперированный строй). Хотя практическая настройка во многих случаях и не достигает идеального качества, большой точности установки интервалов, можно установить те основные принципы, на которых она базируется. Эти принципы относительно просты и с научной точки зрения безупречны.
Теоретически достаточно просто подсчитать частоты любого музыкального звукоряда, если опираться на какую-либо заранее предписанную схему. Прежде всего необходимо установить исходную частоту, так сказать, точку отсчета, то есть необходимо задать определенное числовое значение частоты для какого-либо выбранного тона. Обычно таким тоном является ля первой октавы.
По частоте выбранного отправного тона определяют частоты всех других тонов октавы, которые должны соответствовать строю инстру-мента. Укажем здесь, что в чистом строе настраиваются такие инструменты, как скрипка, арфа, некоторые виды гармоний; в равномерно-темперированном строе — клавишные, язычковые инструменты. Каким же образом можно определить соотношения частот тонов в обоих строях? Небольшой экскурс в историю поможет нам лучше разобраться в этом вопросе [4].
Древнейшие звукоряды у греков были построены на основе квинтовых и октавных ходов; для получения интервалов октавы и квинты достаточно было изменить длину струны в определенной пропорции (октава — 1/2 длины струны; кварта —3/4 и квинта — 2/3). Так как частоты звуков обратно пропорциональны длинам звучащих частей струн, то для древнейшего звукоряда, положенного, по преданию, в основу настройки арфы Орфея, получим ряд интервальных коэффициентов для нахождения частот по частоте основного тона (до), коэффициент которого равен 1:1.
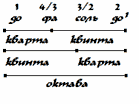
Основных интервалов здесь два — квинта и октава. Кварта (фа) теоретически может быть получена, если взять квинту от основного тона вниз, а полученный звук перенести на октаву вверх. Звуковысотные интервалы складываются и вычитаются, при этом их интервальные коэффициенты умножаются друг на друга или делятся. Например, кварта+квинта=октава соответствует 4/3 х 3/2 = 2.
Пользуясь основными интервалами — квинтой и октавой, можно расширить полученный звукоряд. Если от тона звукоряда соль с интервальным соотношением 3/2 сделать ход на квинту вверх, а от тона фа (4/3) — ход на квинту вниз, то после переноса обоих новых тонов в пределы октавы получим:
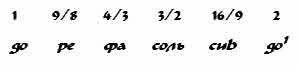
В этом звукоряде представлены интервалы: прима, секунда, кварта, квинта, малая септима, октава. Последующие ходы по квинтам дают возможность получить болышую терцию и большую сексту. Этот строй был известен философам школы Пифагора (V—VI вв. до н. э.) и был целиком построен по квинтовым ходам.
Используем для нахождения частоты тонов пифагорова строя оба его основных требования — чистые квинты 3:2 (1,5:1) и чистые октавы 2:1, взяв последовательно от самой низкой ноты Ля2 двенадцать квинтовых ходов и семь октавных ходов вверх. Получим: Ля2 — 27,5; Ми1 — 41,25; Си1 — 61,87; Фа-диез — 92,81; до-диез — 139,22; соль-диез — 208,83; ре-диез1 — 313,24; ля-диез1 — 469,86; фа2 — 704,79; до3 — 1057,19; соль3 — 1585,79; ре4 — 2378,68; ля4 — 3568,02 Гц. Здесь мы последовательно умножали исходную частоту 27,5 Гц на квинтовое отношение 1,5. Октавный ряд построим простым удвоением той же частоты: Ля2 — 27,5; Ля1 — 55; Ля — 110; ля — 220; ля1 — 440; ля2 — 880; ля3 — 1760; ля4 — 3520 Гц.
Мы приходим к такому выводу, что правила пифагорова строя внутренне противоречивы — для частоты одного и того же тона ля4 получили два разных значения: 3568 и 3520 Гц, то есть строй не замкнулся и после нахождения частот всех двенадцати тонов разница достигла 48 Гц. Найдем частоту тона ля первой октавы, разделив эти числа на 8, получим соответственно 446 и 440 Гц. Разница в 6 Гц, отнесенная к полосе частот целого тона, равная здесь 50,8 Гц, составит несколько менее 1/8 тона. Эту величину расхождения строя называют пифагорейской (или пифагоровой) коммой. Наличие коммы ведет к акустическому недостатку.
Недостатком пифагорова строя является неблагозвучие терции, которая имеет слишком большое число биений и не пригодна для полифонической музыки. Поэтому в XVI веке в Италии был предложен чистый строй, основу которого составляли, наряду с чистыми октавами, квинтами и квартами, также и чистые большие терции с соотношением частот 5:4. Их особенность — сочное звучание в гармонических интервалах. Большой терции пришлось ждать почти полторы тысячи лет, прежде чем музыканты и теоретически и практически признали ее консонирующим интервалом.
В чистом строе диатоническая гамма имеет такие интервальные коэффициенты:


Чистый строй, как и пифагоров, не замкнут, так как не имеет энгармонически равных звуков. В этом строе, например, до-бемоль не совпадает с си. Интервалы чистого строя больше или меньше одноименных интервалов пифагорова строя примерно на величину 1/10 тона, которая называется дидимовой коммой. Если строить звукоряды от каждого нового тона в соответствии с приведенными выше коэффициентами для мажорной и минорной гамм, то каждый раз будем получать иные частоты для тонов. Это делает невозможным модуляции из одной тональности в другую и затрудняет создание музыкальных инструментов с фиксированной частотой звуков.
Поиски замкнутого строя, дающего возможность модуляций, привели к появлению равномерно-темперированного строя. Зарождение равномерно-темперированного строя можно проследить в глубокой древности. Еще греческий философ Аристоксен, ученик Аристотеля, предложил в IV веке до н. э. заменить строй Пифагора делением чистой кварты на пять равных полутонов, как и в современном равномерно-темперированном строе. Согласно Н. Шерману, впервые систему равномерной темперации предложил и ввёл в практику органно-клавирного исполнительства в 1533 г. итальянец Джованни Мария Ланфранко.
Расчёты частот на основе принципа деления октавы на двенадцать равномерных полутонов впервые были выполнены французом Мареном Мерсенном в 1636 – 1637 гг. Мир впервые узнал о фундаментальной константе, не менее знаменитом теперь, чем число π=3.14, интервальном коэффициенте полутона, с помощью которого основной интервал октаву можно разделить на 12 одинаковых интервалов и рассчитать шкалу частот равномерно-темперированного строя:
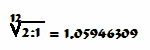
Однако строй Ланфранко – Мерсенна еще долго не был общепризнан и не воспринимался музыкантами того времени: Со времён Ланфранко прошло почти двести лет до появления в 1722 году «Хорошо темперированного клавира» И.С. Баха, который постоянно и настойчиво пропагандировал равномерно-темперированный строй.
Родоначальники равномерной темперации ввели настройку квинт с уменьшением их ширины по сравнению с чистым интервалом на 1/12 пифагорейской коммы, то есть на 1/8,5 1/12 = 1/102 тона. Понятие «темперация» означает выравнивание интервальных соотношений между ступенями звуковой системы.
Отношения частот двенадцати тонов в равномерно-темперированном строе можно приблизительно выразить следующими дробями, полученными еще Гельмгольцем [9] и в дальнейшем несколько уточненными: 1/1; 89/84; 55/49; 44/37; 63/50; 295/221; 99/70; 442/295; 100/63; 37/22; 98/55; 168/89; 2/1.
В таблице 1 сравниваются интервальные коэффициенты для получения частот звуков чистого и равномерно-темперированного строев построением интервалов от тона до. Величина интервалов дана также в центах.
Примечание Цент — одна из единиц для измерения звуковысотных интервалов. Один полутон равен 100 центам. Цент — логарифмическая единица; его величина, выраженная в единицах частоты — герцах, увеличивается от нижних частот к верхним. Так, один цент в области ля1 равен примерно 0,26 Гц, а в области ля = 0,13 Гц.
Как видно из таблицы 1, полутон в чистом строе в зависимости от его положения в октаве имеет разную величину. В равномерно-темперированном строе все полутоны равны.
Таблица 1
| Ноты | Чистый строй | Темперированный строй | Ошибка | ||
| отношение частот | интервал, цент | отношение частот | интервал, цент | ||
| до | 1,00000 | 1,00000 | 0,0 | ||
| до# | 1,04166 | ||||
| реЬ | 1,08000 | ||||
| ре | 1,12500 | 1,12246 | 0,25 | ||
| ре# | 1,17187 | ||||
| миЬ | 1,20000 | ||||
| ми | 1,25000 | ||||
| фаЬ | 1,28000 | ||||
| ми# | 1,30208 | ||||
| фа | 1,33333 | ||||
| фа# | 1,38889 | ||||
| сольЬ | 1,44000 | ||||
| соль | 1,5000 | 1,49831 | 0,12 | ||
| соль# | 1,56250 | ||||
| ляЬ | 1,60000 | ||||
| ля | 1,66667 | 1,68179 | 0,91 | ||
| ля# | 1,73611 | ||||
| сиЬ | 1,80000 | ||||
| си | 1,87500 | ||||
| доЬ | 1,92000 | ||||
| си# | 1,95313 | ||||
| до1 | 2,00000 |
С помощью интервальных коэффициентов высчитаны частоты тонов малой октавы (4 тона), первой и второй октав (3 тона) равномерно-темперированного строя для двух эталонов частоты 440 и 435 Гц, см. таблицу 2. Для сравнения даны также и частоты тонов чистого строя (за точку отсчета взят тон до1 = 261,62 Гц).
Таблица 2
| Ноты | Равномерно-темперированный строй | ЧистыйстройГц | |
| ля1=440 Гц | ля1=435 Гц | ||
| соль# | 207,65 | 205,29 | -- |
| ля | 220,00 | 217,50 | -- |
| ля# | 233,08 | 230,43 | -- |
| си | 246,94 | 244,13 | -- |
| до1 | 261,62 | 258,65 | 261,62 |
| до# | 277,18 | 274,03 | -- |
| ре1 | 293,66 | 290,33 | 294,32 |
| ре#1 | 311,13 | 307,59 | 313,95 |
| ми1 | 329,63 | 325,88 | 327,02 |
| фа1 | 349,23 | 345,26 | 348,82 |
| фа#1 | 369,99 | 365,79 | -- |
| соль1 | 391,99 | 387,54 | 392,43 |
| соль#1 | 415,30 | 410,59 | 418,60 |
| ля1 | 440,00 | 435,00 | 436,03 |
| ля#1 | 466,16 | 460,87 | 490,54 |
| си1 | 493,88 | 488,27 | 490,54 |
| до2 | 523,25 | 517,31 | 523,20 |
| до#2 | 554,36 | 548,06 | -- |
| ре2 | 587,33 | 580,65 | -- |
Именно этот диапазон (соль-диез — ре2) или более узкий ля — ля1 настройщик фортепиано темперирует в первую очередь, и от правильной настройки этого диапазона зависит правильность настройки всего инструмента в целом.
Частоты тонов, выходящих за пределы таблицы, легко могут быть получены октавными ходами вверх или вниз с удвоением частоты при повышении на октаву и делением частоты вдвое при понижении на октаву (см. частоты звуков равномерно-темперированного строя в приложении). Действительные же частоты тонов, полученные после настройки инструмента, близки к табличным, но полного совпадения никогда не бывает по причинам, которые будут рассмотрены ниже.
Надо сказать, что, с музыкально-акустической точки зрения, и чистый, и равномерно-темперированный строй имеют существенные недостатки, выявляющиеся в процессе исполнения музыки. Благозвучие интервалов и аккордов чистого строя, их красота и сочность, которые высоко оцениваются музыкантами и слушателями, представляют в музыкальной практике исключение. Одни только чистые интервалы не всегда получаются даже на инструментах со свободной интонацией, не говоря уже о темперированном строе, в котором нечистое звучание аккордов уже заложено в системе настройки. И дело не только в квалификации исполнителя, совершенстве его интонационного мастерства. Теоретически невозможно исполнять одни чистые интервалы во всем диапазоне музыкального инструмента.
Поясним сказанное примерами. Подсчитаем разностные тона для чистого и темперированного аккорда. Возьмем, к примеру, мажорный аккорд ля1 — до-диез2 — ми2:440, 550 (=440 * 5/4) и 660 Гц (=440 * 3/2). Получим следующие разностные тоны: 550—440=110, 660—550 = 110 и 660—440=220 Гц. Таким образом, в приведенном чистом аккорде можно услышать разностные тоны 110 и 220 Гц. При небольшой неточности интонирования чистого аккорда появившиеся отклонения частот еще малозаметны. Высчитаем теперь разностные частоты того же аккорда, но составленного из темперированных тонов. Для ля1 оставляем ту же частоту 440 Гц, для до-диез2 — 554,4 (=440 * 1,26) и для ми2 — 659,26 (=440 * 1,4983) Гц. Соответствующие разностные тоны будут: 554,4—440 = 114,4 Гц, 659,26— 554,4 = 104,86 Гц и 659,26—440 = 219,26. Все три разностных тона имеют отличающиеся частоты, что и даст заметные на слух биения в аккорде.
Чистые аккорды можно слышать в игре квартетов смычковых инструментов, в многоголосии квалифицированных певческих ансамблей. Но во многих случаях в болыших хоровых ансамблях не придерживаются строго чистой интонации. Это особенно заметно в хоровом исполнении на радио. Каждый отдельный певец имеет индивидуальное представление о высоте тона и модулирует, кроме того, высоту звука вибрато. При этом сдвиг частоты достигает более полутона. В результате даже в унисонах существуют широкие полосы высот, которые в целом приводят к шумовому гудению, «клокотанию», и слушатель с трудом обнаруживает правильный тон. Нередко и дирижеры смотрят на такое нечистое исполнение как на неизбежное зло.
При пении интонационные отклонения, дающие биения не более 10 Гц, еще не обнаруживают особой шероховатости. Грубое, нечистое звучание, создающее впечатление «бурления», возникает тогда, когда частота биений достигает примерно 16 в секунду, что может восприниматься как низкий разностный тон. Определенные проблемы возникают и при исполнении музыки мелодического склада, для которой чистый строй считается наилучшим.
Нормальная высота настройки любого инструмента, ансамбля, хора — это частота ля1=440 Гц. Она определена стандартом. Это действительно так, и в отношении настройки инструментов с фиксированным звукорядом иных мнений не должно быть: пианино, рояли, аккордеоны, баяны, гитары и т. д. должны быть настроены в соответствии со стандартом. Но вот оказывается, музицирование в чистом или пифагорейском строе не может выполнить требования постоянства высоты ля1 440 Гц. В чем тут дело? Построим примеры ходов по чистым интервалам с периодическим возвратом к тону ля1. Возьмем такую последовательность интервалов:
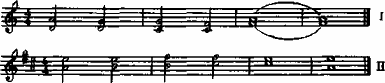
Последовательность чистых интервалов.
Вычислим полученные частоты тонов. Если все интервальные ходы построены чистыми интервалами, то тон ля1 в верхнем примере оканчивается с частотой 434,57 Гц, а в нижнем — с частотой 445,5 Гц. Соответственно, на — 5,43 Гц ниже и 5,5 Гц выше нормы 440 Гц. Можно было бы привести другие примеры и убедиться в появлении все новых и новых значений частоты для тона ля1. С теоретической точки зрения, таких новых частот ля1 может быть получено бесконечное множество. Можно подобрать такие музыкальные примеры, в которых при чистом строе отклонения тона ля1 достигнут более плюс-минус полутона. Это обстоятельство, которое можно подтвердить экспериментальными измерениями частоты, должно учитываться в хоровой практике.
Если бы мы захотели найти место каждого чистого интервала в одной системе, то есть построенной от одной исходной частоты, то убедились бы, что это невозможно. Иными словами, ни музыкальный инструмент, ни певец не в состоянии в сколько-нибудь сложной музыке исполнить все интервалы произведения в чистом строе одной системы. В зависимости от последовательности ходов чистых интервалов встречающиеся одноименные тона по частоте будут различаться. Следовательно, исполнение музыки на инструментах со свободной интонацией чистыми интервалами возможно только с использованием множества систем чистого строя, когда из каждой такой системы берутся только один чистый интервал и его обращение.
В определенном смысле мы будем не очень далеки от истины, если скажем, что реально в настройке существует только равномерно-темперированный строй (или, по крайней мере, то, что приближается к нему). Действительно, ни один музыкальный инструмент не настроен полностью в системе пифагорова строя или чистого строя. Да, на инструментах со свободной интонацией музыкант берет чистые интервалы, но все эти чистые интервалы относятся не к одной какой-либо системе пифагорова или чистого строя, а ко многим системам, для которых частоты одноименных тонов не совпадают ни теоретически, ни практически (другое дело, что разница может и не быть большой). Музыкант играет отдельные чистые интервалы, относящиеся к разным системам.
Только при игре в равномерно-темперированном строе частота исходного тона ля1 сохраняется при любых модуляциях из одной тональности в другую.
Однако исполнительство в чистом и в пифагоровом строях имеет все же и практическое значение в музыкальной практике сегодняшнего дня. Поэтому приходится решать, нужно ли требовать точного соблюдения высоты тона ля1 440 Гц? Как норма для настройки, такая высота тона может быть выдержана с необходимой точностью. Но если требовать при пении а саррелла соблюдения 440 Гц.во всех случаях, то это равносильно требованию петь, употребляя только равномерно-темперированные интервалы. Ни о каком благозвучии чистых интервалов в этом случае говорить не придется. Единственно, чего нужно добиваться,— это соблюдения общей средней высотьг ля1 в исполняемом произведении.
Иногда некоторые музыканты требуют настроить инструмент с фиксированным звукорядом, чистыми квинтами, забывая о том, что получающийся при этом строй является незамкнутым и осуществить такую настройку нельзя.
Каким же образом настройщик получает нужную в инструменте высоту тона? Основное средство — слуховой контроль биений. В качестве критерия настройки в унисон удобно использовать контроль числа биений в секунду. Обычно рекомендуется считать биения в течение, например, 10 с, но это не совсем точный метод, так как трудно различить дробные части биений. Лучше удается подсчет биений, если с помощью секундомера измерить время определенного числа биений, если, конечно, они не слишком часты. Существуют электронные метрономы с индикацией ритма световыми вспышками. С помощью такого метронома можно синхронизировать биения с частотой вспышек и по шкале метронома, предварительно отградуированной, получить отсчет числа биений. Механический метроном для этой цели непригоден, так как его громкие щелчки будут только маскировать биения. Слишком быстрые или, наоборот, слишком медленные биения контролировать трудно. Обычно считается, что точность счета достаточна при числе биений от одного за 10 с до нескольких биений за 1 с. При известной тренировке и соответствующем опыте настройщикам удается контролировать 5, 10 и даже 20 биений в секунду, но в таком случае биения не считают, а запоминают характер их звучания, то есть ту окраску звука, которую придают интервалу соответствующие биения.
Достаточно легко подсчитать биения и меньше двух в секунду, но не у любого инструмента это возможно, так как чем реже биения, тем длительнее должно быть звучание для их подсчета. Не все инструменты по своему принципу звукообразования обеспечивают достаточное для этой цели время звучания. Легко заставить звучать практически как угодно долго язычковый инструмент и очень точно настроить его, но подобного преимущества нет у фортепиано. Даже басовые струны, имеющие самое большое время звучания, находятся в колебании примерно 40—50 с у рояля и всего 20—25 с у пианино. Теноровые струны колеблются примерно 10 с, а самые короткие дискан-товые струны около 1 с. Фактически же пригодное для прослушивания время еще меньше, если учесть, что необходимо также слушать биения между обертонами, затухающими быстрее основного тона струны. Биения, которые для своего определения требуют времени больше, чем звучит струна, уже нельзя подсчитать с высокой точностью.
Мы теперь знаем, какие частоты должны излучать музыкальные инструменты, рассчитать это было делом сравнительно нетрудным. Более трудная задача состоит в обеспечении требуемой высоты тонов в процессе настройки. В технической литературе часто отсутствуют указания, как же достичь выполнения предложенных там рекомендаций практически. И не многие настройщики в состоянии правильно разъяснить, что же скрывается за теми обычными операциями, которые осуществляются при настройке музыкальных инструментов. К рассмотрению этих вопросов мы и приступаем в следующем разделе.
2. Физическая сущность настройки интервалов
Тоны определенной высоты получают посредством настройки интервалов с помощью контроля биений. Основные интервалы, используемые при настройке, – это прима (унисон), октава, квинта, кварта, большая и малая терции, большая и малая сексты, большая децима. Музыкальные звуки, как известно, сложны по своему составу, то есть содержат ряд гармонических составляющих, кратных по частоте основному тону. В этом нетрудно убедиться при помощи флажолетов. Если, например, слегка коснуться пальцем точно середины струны и после ее щипка сразу же снять палец со струны, мы явственно услышим вторую гармонику.
Если место касания расположено на одной трети длины струны, то подобным же образом получим ясно слышимую третью гармонику. Этот опыт наглядно показывает наличие множества простых тонов, составляющих сложный звук струны. Поэтому когда камертон имеет частоту, близкую к частоте первой гармоники, то есть основного тона струны, то биения возникают между этими двумя частотами. Возьмем другой камертон, близкий по частоте ко второй гармонике той же струны, – биения будут образовываться уже между звуком камертона и этой второй гармоникой и т. д. Так можно «прощупать» до десятка гармоник сложного звука. И везде, где в звуках интервала окажутся унисоны (примы) между какими-либо гармониками, эти унисоны при не совсем точной их настройке обязательно дадут биения. Поэтому наша задача будет заключаться в нахождении унисонов в интервалах, независимо от того, какие гармоники дают эти унисоны. Гармоники, создающие унисон, называют совпадающими, независимо от точности этого унисона.
Если настраивать струну по камертону, то возникает один вид биений, а именно — между основными тонами струны и камертона. (Хотя в реальности, можно услышать и высокочастотные биения).
А что мы услышим, когда одну струну будем настраивать по другой в унисон? Здесь уже становятся заметными биения, как между первыми гармониками, так и между вторыми и третьими. Стоит слегка расстроить частоты совпадающих гармоник, как между ними возникнут биения с частотой, определяемой разностью частот этих гармоник. Сравним, например, гармонические ряды для струн, первые гармоники которых не совсем точно настроены, в единицах Гц:
440 880 1320 1760
439 878 1317 1756
Нетрудно подсчитать биения между соответствующими парами гармоник — они равны 1, 2, 3, 4 биений в секунду. Следовательно, одновременно должно быть слышно несколько видов биений. Внимательное вслушивание в слегка расстроенный хор струн или язычков подтверждает данный вывод. Обычно хорошо слышны два-три вида биений, различающихся между собой как по громкости, так и по частоте.
Естественно, что моменты синфазности для разных пар совпадающих гармоник приходятся на разное время. Если, например, первые гармоники в один момент времени находятся в антифазе, то они ослабляют друг друга, громкость их мала, и в этот момент времени лучше слышны совпадающие гармоники более высокого порядка, находящиеся в состоянии синфазности. Можно заметить даже как бы скачкообразное, на мгновение, повышение тона на октаву. Добавление к двум струнам третьей (в унисон) изменяет картину биений, они становятся как бы «размазанными», нечеткими; звучание трех струнного хора, таким образом, может замаскировать ошибки настройки.
Иногда слышны биения и в одной струне, что затрудняет настройку. Причин этого явления может быть много. Это — овальность поперечного сечения струны, неравномерность распределения плотности материала по длине, несколько различная в разные моменты времени плоскость колебаний (вращение струны при колебаниях), неплотная посадка конца рабочей части струны на штифт штега (деревянный брусок со штифтами, приклеенный к резонансовой деке) пианино или рояля, плохая обработка клангштабика (ребро отсечки струны) на чугунной раме — нечеткая линия отсечки струны, вызывающая изменение длины колеблющейся части струны при больших амплитудах, близкое совпадение одной из резонансных частот деки с частотой струны, что приводит к появлению биений и т. д. Эти биения устранить довольно трудно, замена струны не всегда помогает. Неустранимые биения могут появиться и в результате взаимодействия двух или трех струн. Это произойдет в том случае, если невозможно совместить по частоте все гармоники струн одновременно. Так мы добьемся устранения биений между первыми гармониками струн, но могут остаться при этом биения между другими гармониками, если их частоты не совпадут одновременно с совпадением первых гармоник. Причинами могут быть различная длина струн в хоре, различная жесткость материала керна, различный диаметр струн и др.
Проверка точности настройки струн в унисон клавишных и язычковых инструментов показывает, что абсолютно точного унисона не существует. Даже высококвалифицированные настройщики часто оставляют в унисонах десятые доли биений в секунду. Объясняется это невозможностью достижения идеального результата и тем, что расстройка сознательно допускается настройщиками для «оживления» звука. Незначительная, еле уловимая расстройка унисонов благоприятно сказывается на тембре звука, делает его ярче, выразительнее, полетнее. Но важно не перейти границу, за которой начинается плохая настройка. О точности настройки скажем в следующих разделах.
После настройки унисона обычно следует настройка октавы. Какие биения слышны в октаве? Мы знаем, что соотношение частот нот в октаве 1:2 (или 2:1, что то же самое), поэтому подходящим примером для октавы будут такие, например, два звука со следующими частотами гармоник, Гц:
| ... | ||||
| ... | ||||
| ... |
Самыми близкими частотами, между которыми могут возникать биения в октаве (при неточной настройке), как показывает данный пример, обладают вторая гармоника первого звука и первая гармоника второго звука, то есть гармоники с частотой 880 Гц.
Приведенные выше числовые примеры содержат интересную закономерность: в унисоне соотношение частот основных гармоник 1:1, и биения возникают между первой гармоникой одного звука и первой гармоникой второго звука (1 и 1). Далее, в октаве отношение частот 1:2, и биения возникают между первой гармоникой верхнего звука и второй гармоникой нижнего звука (1 и 2). Продолжая рассуждать таким образом, легко вывести правило, по которому, зная интервальный коэффициент, можно сразу сказать, между какими гармониками, составляющими интервал звуков, образуются биения. Надо только учесть, что большее число в интервальном коэффициенте соответствует номеру гармоники нижнего звука, а меньшее — номеру гармоники верхнего звука интервала.
Выпишем коэффициенты основных консонансных интервалов натурального звукоряда гармоник — именно они используются в настройке.
| унисон | октава | квинта | кварта | терция б. | терция м. | секста б. |
| 1:1 | 1:2 | 2:3 | 3:4 | 4:5 | 5:6 | 3:5 |
Последовательность расположения интервалов в натуральном звукоряде легко прослеживается, если записать в нотном обозначении гармоники, например, от ноты до большой октавы:

Гармоники ноты
Таким образом, в натуральном звукоряде интервалы располагаются в следующем порядке: унисон, октава, квинта, кварта, большая терция, малая терция, малая терция, большая сёкунда, большая секунда и т. д. Зная последовательность интервалов между гармониками, достаточно просто написать натуральный звукоряд от верхней и нижней ноты выбранного интервала и установить гармоники, образующие в этом интервале унисон. Покажем это на примере квинты (ре1 –ля1) и кварты (ре1 – соль 1):
| Интервал | Номера гармоник | |||||
| квинталяре | ля1 | ля2 | ми3 | ля3 | до4 | ми4 |
| ре1 | ре2 | ля2 | ре3 | фа3 | ля3 | |
| квартасольре | соль1 | соль2 | ре3 | соль3 | си3 | ре4 |
| ре1 | ре2 | ля2 | ре3 | фа3 | ля3 |
Из таблицы наглядно видно, что в интервале квинты унисон образуется между второй гармоникой верхнего звука и третьей гармоникой нижнего звука, а в интервале кварты — между третьей гармоникой верхнего звука и четвертой гармоникой нижнего звука (в таблице для квинты — это ля2— ля2, для кварты — ре3— ре3). Тон ля2 называется тоном совпадения звуков ля1 и ре1 аналогично ре3— тон совпадения звуков соль1 и ре1. В других интервалах тоны совпадения устанавливаются таким же способом.
Вернемся еще раз к биениям обертонов. Предположим, например, что мы слушаем правильно настроенную темперированную квинту ре1 — ля1 с частотами основных тонов 293,66 и 440,00 Гц соответственно. Предположим для простоты рассуждений, что обертоны кратны основным тонам. Тогда получим следующие два гармонических ряда, Гц:
| ля1 | ...Гц | ||||||
| ре1 | 293,66 | 587,33 | 880,99 | 1174,66 | 1468,32 | 1761,99 | ...Гц |
Нетрудно заметить, что частота биений между второй гармоникой верхнего звука и третьей гармоникой нижнего звука будет равна 880,99 – 880=0,99 или округленно 1 Гц. Но биения дадут также четвертая гармоника верхнего звука с шестой гармоникой нижнего звука. Эти биения, хотя они и более слабые по сравнению с нижними биениями, будут достаточно хорошо слышны и иметь частоту 1761,99 – 1760 = 1, 99 или округленно 2 биения в секунду, то есть в два раза чаще. Если не представлять себе акустические процессы, происходящие при колебаниях струн в настраиваемом интервале, то легко ошибиться и принять за ориентир верхние биения, сводя их частоту к 1 биению в секунду. В итоге квинта будет темперирована неправильно.
Верхние более частые биения, в конечном счете, не только не мешают настройке, но и помогают более точно установить зону темперации интервала и величину темперации. Важно только уметь переключать на них внимание. Переключение необходимо на подходе к точной темперации интервала, когда нижние биения из-за их растянутости на фоне общего затухания тонов становятся более трудными для контроля, в то время как верхние биения очень четко слышны и нужно только оставлять их в два раза более частыми, по сравнению с частотой нижних биений. Ориентировке помогает и то обстоятельство, что верхние биения звучат на октаву выше (сравните частоту второй и четвертой гармоники ля1, а также третьей и шестой гармоники ре1 в вышеприведенном примере).
Что удивительно, – в популярных брошюрах, пособиях по настройке, авторы которых прекрасно знают настройку, ничего не говорится об этом важном для обучения моменте – «многоголосии биений», с которым неизбежно сталкивается любой начинающий настройщик, который только после многочисленных проб и ошибок, блужданий и неуверенности в овладении темперированием интервалов начинает понимать (но это не всегда бывает) роль и значение верхних биений в настройке квинт и кварт, начинает их использовать. Правило удвоения частоты для верхних биений легко запоминаемо, и если в среднем квинту надо темперировать по 1 биению в секунду, а кварту по 1,4 биения в секунду, то частота верхних биений в среднем будет соответствовать 2 биениям в секунду и 2,8 биений в секунду. Этот момент, кажется, является новым в теории настройки (но не в практике квалифицированных настройщиков, которые, однако, о нем не любят распространяться).
Полноправное введение верхних биений квинт и кварт в процесс настройки облегчит и ускорит овладение начинающими настройщиками техникой настройки. Это — прекрасная иллюстрация общеизвестного философского тезиса о том, что нет ничего практичнее хорошей теории.
Мы уже знаем, что темперация — уход от чистых интервалов — сопровождается появлением биений. Как правильно выбрать необходимое направление темперации и частоту биений? Как посчитать биения?
Это нетрудно сделать, взяв за основу прослеженную выше связь числителя и знаменателя интервального коэффициента с номерами гармоник, дающих биения. При этом необходимо знать частоты первых гармоник (основных тонов), рассчитанные выше для равномернотемперированного строя с помощью интервального коэффициента 1,05946309. Общую формулу для подсчета биений выведем на примере квинты. В квинте частота третьей гармоники нижнего звука равна 3fн, где fн — частота основной гармоники нижнего звука, а частота второй гармоники верхнего звука — 2fв, где fв — частота основной гармоники верхнего звука. Отсюда определим частоту биений как разность 2fв – 3fн.
Пусть мы хотим получить квинту с частотами первых гармоник 200,3 и 300 Гц (частоты выбраны лишь для примера и не соответствуют какой-либо реальной ноте). После подстановки получим: 2 х 300–3 х 200,3=600–600,9= – 0,9 биений в секунду. Знак минус перед результатом показывает, что чистый интервал должен быть уменьшен примерно на одно биение в секунду, как это необходимо для темперированной квинты. Обозначим частоту биений fб, тогда получим следующее выражение для подсчета биений в любых темперированных интервалах:
fб = mfв – nfн (9)
где fви fн– частоты основного тона верхнего и нижнего звуков соответственно (их берут из шкалы частот равномерно-темперированного строя); m и n - числитель и знаменатель интервального коэффициента, в котором первым поставлен верхний звук (например, в квинте 2:3, где m=2, n=3).
[Интервальный коэффициент для интервала, в котором первый звук выше второго (интервал направлен вниз), есть величина, обратная коэффициенту для того же интервала, направленного от нижнего звука к верхнему].
При таком методе определения необходимого числа биений в интервалах положительное значение разности (знак +) покажет, что данный интервал шире соответствующего чистого интервала, а отрицательное значение (знак – ) будет указывать на то, что данный интервал уже чистого.
Нет необходимости каждый раз делать подсчет числа биений темперирован<
Дата добавления: 2021-03-18; просмотров: 1110;











