Применение МАИ-МАС в анализе задач морских перевозок
К числу важнейших задач морских перевозок относится задача формирования (определения) фрахтовой ставки. Согласно работ [3, 5, 26, 31] основными факторами, влияющими на ее определение являются скорость судна, его грузоподъемность и мощность энергетической установки. Тенденция современного судоходства характеризуется увеличением скорости судов, так как чем выше стоимость перевозимого груза, тем больше будет прибыль от сокращения сроков поставки. Так, например, в линейном судоходстве средняя скорость составляет 20–22 узла, а скорость контейнеровозов достигает 36 узлов [13]. Вместе с тем, рост цен на топливо и горюче-смазочные материалы в настоящее время составляют 55% – 60% расходов на рейс определяют тенденцию к снижению скорости судов, которая по мнению авторов работы [13] будет находиться в пределах 14–16 узлов.
На грузоподъемность разных типов судов большое влияние оказывают партионность груза, его ценность, общая схема перевозки, техническая оснащенность и нормы грузовых работ портов и др. Следует отметить, что в связи с ростом размеров судов стоимость перегрузки навалочных грузов в портах увеличилась втрое за последние 15 лет [13]. В большей степени это относится к портам выгрузки, в которых производительность обработки судов ниже, чем в портах погрузки. Это определяется в первую очередь производительностью машин грейдерного типа, возможности которых практически исчерпаны [13].
Важным фактором является также тип и мощность судовой энергетической установки, так как суда одного назначения могут иметь различные установки, что определяется не столько родом груза, сколько уровнем технического прогресса. Необходимо также указать на ряд факторов, которые несут в себе явные риски: возраст судна, флаг судна и район плавания [25]. Возраст судна характеризует его техническую пригодность для выполнения рейса и определенную гарантию сохранной доставки груза. Кроме этого во многих портах мира существуют возрастные ограничения на заход судов. Флаг судна определяет его национальную принадлежность и влияет на его возможности захода в различные порты, так как в ряде стран существуют запреты на посещение портов судами под флагом некоторых государств. Оба эти фактора могут повлиять на страхование груза, так как привлечение к доставке товара судна, флаг которого не внушает доверия страховым компаниям может привести к повышению процента страховой премии. Риск, связанный с районом плавания судна, ассоциируется прежде всего с ростом деятельности международного морского пиратства.
Важным фактором, влияющим на величину фрахтовой ставки, является тип судна. Например, для перевозки навалочных грузов (зерна, угля, руды и др.) широко используются балкеры, рудовозы, углевозы [13]. Несмотря на определенные различия между ними в плане размеров, грузоподъемности, скорости, конструктивных особенностей и др., они характеризуются взаимозаменяемостью при перевозке определенных типов грузов. Например, из рассмотрения схемы тяготения основных видов перевозимых морем грузов к типам судов [13], можно видеть, что зерно и другие сельскохозяйственные продукты могут перевозиться балкерами, рудовозами, углевозами. Это говорит о их взаимосвязи. Выполненный анализ позволяет сформулировать и решить ряд задач с применением МАИ–МАС.
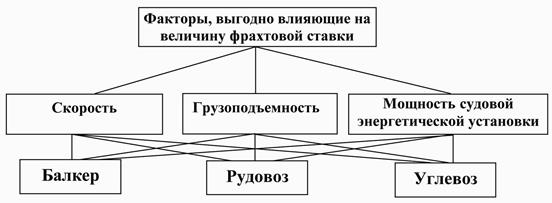
Задача выбора лучшей альтернативы. Декомпозиция данной задачи представлена на рис.2.25-а, где в качестве критериев (K) и альтернатив (А) соответственно выбраны: K1 – скорость; K2 – грузоподъемность; K3 – мощность энергетической установки; А1 – балкер; А2 – рудовоз; А3 – углевоз. Данная иерархия отображает факторы, выгодно влияющие на величину фрахтовой ставки. Для решения используем МАИ, в рамках которого выполняются следующие операции: формируются матрицы парных сравнений (В) между критериями и между альтернативами относительно каждого из критериев с использованием фундаментальной шкалы (табл. 2.10) [35]; определяются значения собственного вектора (d) матрицы; выполняется нормирование значений d и определяются веса векторов приоритетов.
В формализованном виде данную процедуру можно представить так:
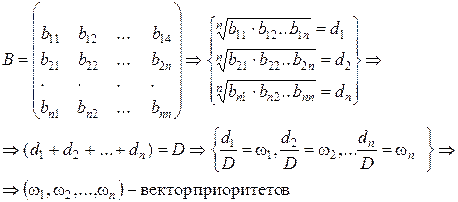 (2.29)
(2.29)
Таблица 2.10
Фундаментальная шкала [35]
| Степень предпочтения | Определение | Комментарии |
| Равная предпочтительность | Две альтернативы одинаково предпочтительны с точки зрения цели | |
| Слабая степень предпочтения | Промежуточная градация между равными и средними предпочтениями | |
| Средняя степень предпочтения | Опыт эксперта позволяет считать одну из альтернатив немного предпочтительнее другой |
Продолжение таблицы 2.10
| Степень предпочтения | Определение | Комментарии |
| Предпочтение выше среднего | Промежуточная градация между средним и умеренно сильным предпочтением | |
| Умеренно сильное предпочтение | Опыт эксперта позволяет считать одну из альтернатив явно предпочтительнее другой | |
| 6 | Сильное предпочтение | Промежуточная градация между умеренно сильным и очень сильным предпочтением |
| Очень сильно (очевидное) предпочтение | Опыт эксперта позволяет считать одну из альтернатив гораздо предпочтительнее другой: доминирование альтернативы подтверждено практикой | |
| Очень, очень сильное предпочтение | Промежуточная градация между очень сильным и абсолютным предпочтением | |
| Абсолютное предпочтение | Очевидность подавляющей предпочтительности одой альтернативы над другой имеет неоспоримое подтверждение |
Таблица 2.11
Таблица значений случайного индекса (СИ) согласованности для матриц разной размерности [35]
| Порядок матрицы суждений | ||||||||||
| Случайный индекс согласованности (СИ) | 0,52 | 0,89 | 1,1 | 1,2 | 1,3 | 1,4 | 1,4 | 1,4 |
Вычисленный из матрицы парных сравнений собственный вектор приемлем в том случае, если ОС ≤ 0,10 (0,20 может допускаться, но не больше). Для матриц порядка n = 3, желательно выполнение условия ОС ≤ 0,05, и для n = 4 – ОС ≤ 0,08. Если отношение согласованности (ОС) превышает значение 0,10, то необходимо глубже изучить проблему и пересмотреть суждения в соответствии с фундаментальной шкалой (табл. 2.10).
Далее выполняется проверка согласованности элементов матрицы В посредством подсчета отношения согласованности (ОС). ОС=ИС / СИ, где ИС = (λmax–n)/(n–1) индекс согласованности; 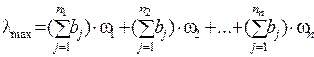 – максимальное собственное число; п – число сравниваемых элементов; СИ – случайный индекс (назначается по таблице 2.11, приведенной в [35]). Для п = 3, СИ = 0,52.
– максимальное собственное число; п – число сравниваемых элементов; СИ – случайный индекс (назначается по таблице 2.11, приведенной в [35]). Для п = 3, СИ = 0,52.
Матрицы парного сравнения для выгод (рис.2.25-а) представлены в табл. 2.12.
а)
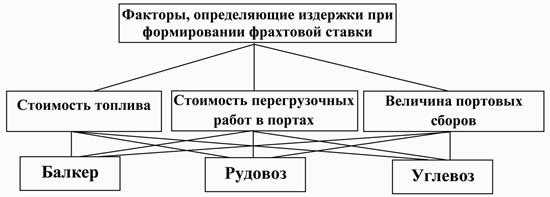
б)
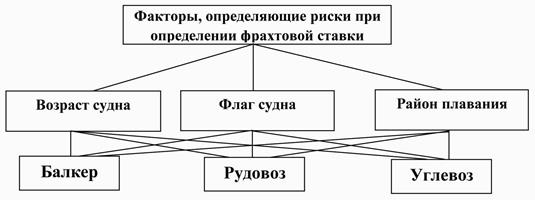
в)
Рис. 2.25. Доминантные иерархии: а) выгоды; б) издержки; в) риски
Таблица 2.12
Дата добавления: 2021-03-18; просмотров: 626;











