Статистического исследования
Объектами статистических исследований являются статистические совокупности, состоящие из отдельных единиц, характеризуемых различными признаками. В результате исследований выявляются статистические закономерности , на основе использования моделей социально-экономических явлений и методов обработки и анализа экономико-статистической информации.
Статистическая совокупность - множество объектов, явлений, объединенных какими-либо общими свойствами (признаками) и подвергающихся статистическому исследованию. Например, совокупность промышленных предприятий страны. Отдельные объекты явления, составляющие статистическую совокупность и называемые единицами совокупности, обладая некоторыми общими признаками, могут различаться между собой по другим признакам. Поэтому совокупности могут быть однородными (качественно однородными) и неоднородными (качественно неоднородными).
В однородной совокупности объекты (единицы совокупности) сходны между собой по существенным для данного исследования признакам и относятся к одному и тому же типу явления. Однородная совокупность, будучи однородной по одним признакам, может быть разнородной по другим.
Элементы (единицы) неоднородной совокупности относятся к различным типам изучаемых явлений. Для неоднородной совокупности исчисление обобщающих характеристик, в особенности в виде средней величины, неправомерно. С помощью метода группировок и метода таксономии в неоднородной совокупности могут быть образованы однородные группы.
Вся совокупность реально существующих объектов, характеризующих какое-либо явление, называется генеральной. Для статистического исследования из генеральной совокупности по определенным правилам может быть отобрана совокупность единиц, которые образуют выборочную совокупностью.
Каждая единица совокупности характеризуется различными признаками - отличительными чертами, свойствами, качеством.
Варьирующий признак - признак, принимающий в пределах статистической совокупности разные значения у единиц статистической совокупности. Это, однако, не исключает повторений отдельных значений (вариантов) признака, у нескольких единиц совокупности значения признака могут быть одинаковыми. Примером варьирующего признака может служить размер месячной заработной платы рабочих предприятия.
Качественный признак(атрибутивный) - признак, отдельные значения которого выражаются в виде понятий, наименований. Например, профессия рабочего (слесарь, сборщик), уровень образования (начальное, среднее, высшее).
Количественный признак - признак, отдельные значения которого имеют количественное выражение (например, себестоимость продукции по различным предприятиям одной отрасли).
Результативный признак - зависимый признак, то есть изменяющий свое значение под влиянием другого, связанного с ним факторного признака.
Факторный признак (фактор) - признак, оказывающий влияние на другой, связанный с ним результативный признак, и обусловливающий его изменение (вариацию). Роль этих признаков в различных задачах может меняться, в одной задача он выступает как факторный, в другой - как результативный. Например, производительность труда выступает фактором изменения (снижения) себестоимости единицы продукции, и в то же время, производительность труда в связи с квалификацией рабочего является результативным признаком.
В результате статистического исследования устанавливается статистическая закономерность, которая рассматривается как количественная закономерность изменения в пространстве и во времени массовых явлений и процессов общественной жизни, состоящих из множества элементов (единиц совокупности). Она свойственна не отдельным единицам совокупности, а всей совокупности в целом. В силу этого закономерность, присущая данному явлению (процессу), проявляется только при достаточно большом числе наблюдений и только в среднем. Таким образом, это средняя закономерность массовых явлений и процессов. В большом числе наблюдений происходит взаимопогашение индивидуальных отклонений от средней в ту и другую стороны, вызванных случайными причинами, и проявляется закономерность. Это связывает статистическую закономерность с законом больших чисел, По мере увеличения пространственно-временных интервалов развития явления его закономерность становится все более устойчивой.
Таким образом, зная статистическую закономерность конкретного массового явления, можно с определенной вероятностью предвидеть его дальнейшее развитие, определить величину изучаемого признака (показателя). Однако необходимо учитывать, что значительные изменения условий существования этого явления могут привести к существенным изменениям силы этой зависимости.
В социально-экономической статистике закон больших чисел представляет собой общий принцип, в силу которого количественные закономерности, присущие массовым общественным явлениям, отчетливо проявляются лишь в достаточно большом числе наблюдений. Закон больших чисел порожден особыми свойствами массовых социальных явлений. Последние в силу своей индивидуальности, с одной стороны, отличаются друг от друга, а с другой - имеют нечто общее, обусловленное их принадлежностью к определенному виду, классу, к определенным группам. Единичные явления в большей степени подвержены воздействию случайных и несущественных факторов, чем масса в целом. В большом числе наблюдений взаимно погашаются случайные отклонения в противоположные стороны от закономерностей. В результате взаимопогашения случайных отклонений средние, вычисленные для величин одного и того же вида, становятся типичными, отражающими действие постоянных и существенных факторов в данных условиях места и времени. Тенденции и закономерности, вскрытые с помощью закона больших чисел - это массовые статистические тенденции.
Статистическое исследование социально-экономических явлений осуществляется различными методами с использованием моделей этих явлений.
Моделью называется отображение, аналог явления или процесса в основных, существенных для целей исследования чертах. Процесс создания модели называется моделированием. Модель должна учитывать все важные взаимосвязи, закономерности и условия развития таким образом, чтобы на ее основе можно было выполнить эксперименты, цель которых - определение “поведения” объекта моделирования в различных возможных (часто ненаблюдаемых в действительности) условиях. Экономические явления и процессы моделируются с помощью экономико-математических моделей.
Экономико-математическая модель - описание экономического явления или процесса с помощью одного или нескольких математических выражений (уравнений, функций, неравенств, тождеств). Математические выражения характеризуют важнейшие взаимосвязи явлений и процессов, условия и закономерности их развития, ограничения, требования и т.д. Экономико-математическая модель представляет собой обобщение существенной качественной и количественной информации об объекте анализа и служит базой для проведения расчетных экспериментов, которые позволяют получить различные характеристики и параметры изучаемого объекта для заданных условий его развития. Разработка и применение экономико-математических моделей существенно расширяют возможности экономического анализа. Основные преимущества использования экономико-математических моделей заключаются в следующем:
- одновременный учет в модели большого числа требований, условий и предположений, а также достаточная свобода в пересмотре этих условий в ходе работы с моделью;
- непротиворечивость (совместность) получаемых по модели системы показателей;
- возможность получения вариантов поведения изучаемого явления для широкого диапазона и сочетания исходных условий и предположений (например, вариантов прогноза экономического развития).
Экономико-математические модели по назначению делятся на теоретико-экономические иприкладные модели. Многие прикладные модели являются экономико-статистическими моделями или включают последние в качестве составных частей.
Теоретико-экономические - это экономико-математические модели, предназначенные для качественного анализа экономических систем, процессов и явлений, Значения параметров и даже функциональный вид входящих в теоретико-экономическую модель соотношений обычно не конкретизируется. Выводы, которые получаются с помощью этих моделей, как правило, носят общий характер. Типичным примером является вывод об устойчивости (неустойчивости) изучаемой экономической системы, если ее параметры удовлетворяют определенным требованиям, о существовании (отсутствии) сбалансированных или оптимальных решений. Теоретико-экономические модели широко используются в теоретических экономических исследованиях. В настоящее время построение и исследование теоретико-экономических моделей является предметом математической экономики. Для их исследования применяется развитый математический аппарат (теория дифференциальных уравнений, теория матриц, оптимизационные и теоретико-игровые методы и т.д.).
Экономико-статистическая модель - это система математических соотношений, описывающая некоторый экономический объект, процесс или явление, параметры которой определяются (оцениваются) на основе фактических данных с помощью статистических данных (в отличие от теоретико-экономической модели). Структура и конкретный вид экономико-статистической модели определяются спецификой моделируемого объекта, теоретическими представлениями исследователя, целями исследования, доступностью информации, используемыми методами обработки данных. Процесс построения модели распадается на два взаимосвязанных этапа: определение общего вида соотношений модели и входящих в них переменных и статистическое оценивание значений параметров на основе данных наблюдений. К наиболее часто используемым экономико-статистическим моделям относятся тренды, модели временных рядов, изолированные уравнения регрессии, эконометрические модели. Экономико-статистические модели широко применяются при планировании и анализе экономических систем, исследовании их реакции на изменение внешних и внутренних условий функционирования, а также при прогнозировании и определении различных вариантов будущего развития.
Эконометрическая модель - особый вид экономико-статистических моделей, представляет собой систему одновременных регрессионных (стохастических) уравнений. Линейная эконометрическая модель может быть записана в следующем виде (структурная форма модели):
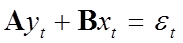 ,
,
где А - невырожденная матрица неизвестных параметров m хm;
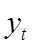 -вектор эндогенных переменных, т.е. переменных, зависящих от
-вектор эндогенных переменных, т.е. переменных, зависящих от
внутренней структуры изучаемого объекта, mх 1;
B - матрица неизвестных параметров m х k;
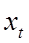 - вектор экзогенных переменных, т.е. переменных не зависящих от
- вектор экзогенных переменных, т.е. переменных не зависящих от
структуры моделируемого объекта, k х 1;
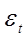 -случайный вектор ненаблюдаемых отклонений;
-случайный вектор ненаблюдаемых отклонений;
t - номер наблюдения (если эконометрическая модель является
динамической, то t обозначает момент времени).
Число эндогенных переменных должно быть равно числу уравнений эконометрической модели. Характерной особенностью эконометрической модели является то, что эндогенная переменная, являясь зависимой переменной в одном из уравнений системы, может быть независимой переменной в другом уравнении эконометрической модели. В развернутом виде эконометрическая модель записывается следующим образом:
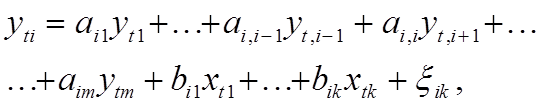
где i = 1,2, ... , m - номер уравнения.
Для оценивания параметров эконометрической модели необходимы специальные методы одновременного оценивания (доказано, что обычный метод наименьших квадратов, примененный к каждому уравнению эконометрической модели изолированно, приводит к несостоятельным оценкам). Наиболее употребительными методами одновременного оценивания эконометрической модели являются двухшаговый и трехшаговый метод наименьших квадратов.
Дата добавления: 2016-12-16; просмотров: 2054;











