Прямоугольная диметрия.

Прямоугольную диметрическую проекцию можно получить путем поворота и наклона координатных осей относительно П¢ так, чтобы показатели искажения по осям X' и Z' приняли равное значение, а по оси Y'- вдвое меньшее. Показатели искажения "k_x" и "k_z" будут равны 0,94, а "k_y"- 0,47.

На практике пользуются приведенными показателями, т.е. по осям X' и Z' откладывают натуральные размеры, а по оси Y'- в 2 раза меньше натуральных.

Ось Z' обычно располагают вертикально, ось X'- под углом 7°10¢ к горизонтальной линии, а ось Y'-под углом 41°25¢ к этой же линии (рис.12.17).

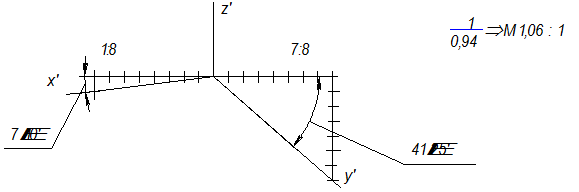
Рис. 12.17

1. Строится вторичная проекция усеченной пирамиды.

2. Строятся высоты точек 1,2,3 и 4.

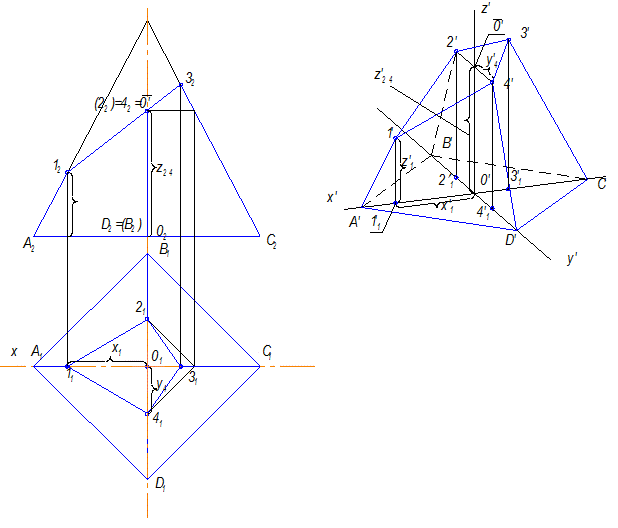
Рис. 10.18

Проще всего строить ось Х¢, отложив на горизонтальной линии 8 равных частей и вниз по вертикальной линии 1 такую же часть.

Чтобы построить ось Y' под углом 41°25¢ , надо на горизонтальной линии отложить 8 частей, а на вертикальной 7 таких же частей (рис.10.17).

На рисунке 10.18 изображена усеченная четырехугольная пирамида. Чтобы построение ее в аксонометрии было проще, ось Z должна совпадать с высотой, тогда вершины основания ABCD будут лежат на осях Х и Y (А и С Î х, В и D Î y). Сколько координат имеют точки 1 и ? Две. Какие? Х и Z.

Эти координаты откладываются в натуральную величину. Полученные точки 1¢ и 3¢ соединяются с точками А¢ и С¢ .

Точки 2 и 4 имеют две координаты Z и Y. Так как высота у них одинаковая, то координата Z откладывается на оси Z'. Через полученную точку 0¢ проводится линия, параллельная оси Y, на которой по обе стороны от точки 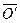откладываются расстояние 0₁4₁ уменьшенное в два раза.

Полученные точки 2¢ и 4¢ соединяются с точками В¢ и D'.