ПРЯМОУГОЛЬНАЯ ДЕКАРТОВА СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ.

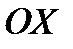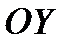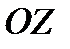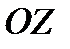ПРЯМОУГОЛЬНАЯ ДЕКАРТОВА СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ ВКЛЮЧАЕТ В СЕБЯ ТРИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ОСИ: ОСЬ АБСЦИСС , ОСЬ ОРДИНАТ , ОСЬ АППЛИКАТ . ОСИ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ -НАЧАЛЕ КООРДИНАТ. ЕЁ ОСИ ОРИЕНТИРОВАНЫ ТАК, ЧТО ЕСЛИ СМОТРЕТЬ ИЗ ПОЛОЖИТЕЛЬНОГО НАПРАВЛЕНИЯ ОСИ НА ПЛОСКОСТЬ 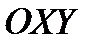, ТО ОС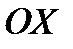И И 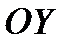РАСПОЛАГАЮТСЯ В ОБЫЧНОМ ПОРЯДКЕ. ДЛЯ ЗАДАННОЙ ПРЯМОУГОЛЬНОЙ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ МОЖНО ОПРЕДЕЛИТЬ ЕДИНИЧНЫЕ ВЕКТОРЫ, НАПРАВЛЕННЫЕ ВДОЛЬ ПОЛОЖИТЕЛЬНЫХ ПОЛУОСЕЙ 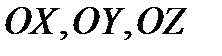. ЭТИ ВЕКТОРЫ ОБОЗНАЧАЮТСЯ КАК 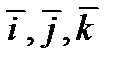. ЗАФИКСИРОВАВ ЭТИ ВЕКТОРЫ, МОЖНО ЛЮБОЙ ВЕКТОР В ПРОСТРАНСТВЕ ПРЕДСТАВИТЬ В ВИДЕ ИХ ЛИНЕЙНОЙ КОМБИНАЦИИ СМОТРИ ДАЛЕЕ ОПРЕДЕЛЕНИЕ 3.3.

ПРИМЕР ОПРЕДЕЛЕНИЯ КООРДИНАТ ТОЧКИ В ПРЯМОУГОЛЬНОЙ ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ. ПУСТЬ В КООРДИНАТНОМ ПРОСТРАНСТВЕ ЗАДАНА ТОЧКА 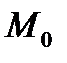(РИС. 5)

СПРОЕКТИРУЕМ ТОЧКУ 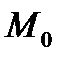НА КООРДИНАТНУЮ ПЛОСКОСТЬ 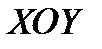. ПОЛУЧЕННУЮ ТОЧКУ 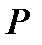СПРОЕКТИРУЕМ НА ОС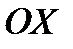И И 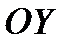СООТВЕТСТВЕННО . ПОЛУЧЕННЫЕ ТОЧКИ (ЧИСЛА) НА ЧИСЛОВОЙ ОСИ НАЗОВЕМ СООТВЕТСТВЕННО:

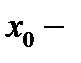АБСЦИССЕЙ ТОЧКИ 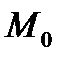, А 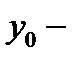ОРДИНАТОЙ ТОЧКИ 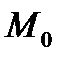. ДАЛЕЕ СПРОЕКТИРУЕМ ТОЧКУ 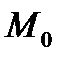НА ОСЬ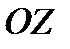

ПОЛУЧЕННУЮ ТОЧКУ (ЧИСЛО) НА ЧИСЛОВОЙ ОСИ НАЗОВЕМ АППЛИКАТОЙ И ОБОЗНАЧИМ 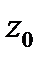. ТРОЙКУ ЧИСЕЛ 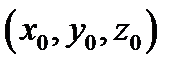В УКАЗАННОМ ПОРЯДКЕ НАЗОВЁМ КООРДИНАТАМИ ТОЧКИ .

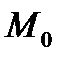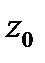
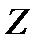
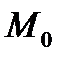
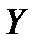
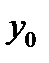
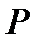
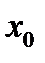
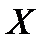
РИС.5

ОПРЕДЕЛЕНИЕ 3.ЛИНЕЙНОЙ КОМБИНАЦИЕЙ ТРЁХ ВЕКТОРОВ 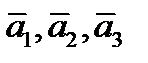НАЗЫВАЮТ ВЕКТОР

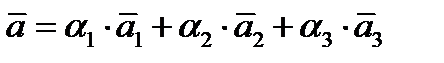(1)